«Кубок Кеплера»

Правильні многогранники — тетраедр, куб, октаедр, ікосаедр, додекаедр — були відомі задовго до Евкліда. Ще піфагорійці, тобто учні і послідовники легендарного Піфагора, перші з яких жили щонайменше за 200 років до Евкліда, вміли будувати принаймні перші чотири з цих фігур. Відкриття додекаедра багато хто приписує філософу Платону, що також жив до Евкліда. Саме завдяки Платону правильні многогранники набули величезної притягальної сили, оскільки відігравали ключову роль у його філософії природи. За Платоном, усе суще в природі утворилося в результаті взаємодії вогню, повітря, води і землі. Найдрібніші структурні елементи (атоми) цих стихій мають форми відповідно правильного тетраедра, октаедра, ікосаедра і куба. Оскільки незадіяним залишався додекаедр, то Платон вважав, що форму цієї фігури має весь Всесвіт. Уже в наш час цю ідею використав відомий іспанський художник-сюрреаліст Сальвадор Далі, зобразивши у своїй «Таємній вечері» знаменитий біблійний сюжет на фоні Всесвіту — додекаедра.

Зрештою, деякі міркування Платона можна інтерпретувати і так, що форму додекаедра мала п'ята, придумана ним стихія — божественний ефір. Пізніше ідея ефіру хвилювала учених протягом багатьох століть, поки врешті-решт не була повністю відкинута з відкриттям на початку XX ст. спеціальної теорії відносності. Але ще й досі чується її відгомін, наприклад, у висловах «в ефірі», «ефірний час» тощо.

Платон мріяв осягнути таємницю взаємоперетворень речовин, встановивши закономірності геометричних перебудов елементів основних стихій. І це, по суті, була одна з перших спроб математичного моделювання в природознавстві. До Платона таким моделюванням займалися піфагорійці. Але їхні моделі були в основному числовими. Наприклад, гармонічно співзвучні акорди піфагорійці пов'язували з пропорційністю довжин струн певним відношенням цілих чисел. Платон же одним з перших запропонував змістовну геометричну модель. А його авторитет сприяв тому, що ця ідея завжди приваблювала дослідників.

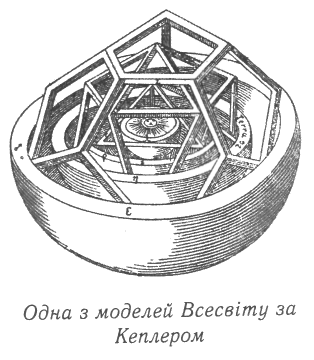
На початку доби нового дослідного природознавства до ідеї використання правильних многогранників у моделюванні природи звернувся знаменитий німецький астроном Йоганн Кеплер (1572-1630). Результатом його пошуків стало декілька так званих «кубків Кеплера», якими символізувалися гармонійні закономірності в розташуванні планетних орбіт. Найвідоміший з «кубків Кеплера» відтворено вище. При його створенні Кеплер виходив ще з давньої гіпотези про рух планет навколо Сонця по кругових орбітах. Весь кубок обмежує велика сфера, якій відповідає орбіта найвіддаленішої з відомих тоді планет — Сатурна. Якщо в цю сферу вписати куб, а в куб — знову сферу, то, за Кеплером, матимемо сферу Юпітера. У сферу Юпітера вписується правильний тетраедр, а вписаною в тетраедр сферою визначається орбіта Марса. Далі послідовно вписується додекаедр, ікосаедр та октаедр, а відповідні вписані сфери визначають орбіти Землі, Венери та Меркурія.

Пізніше, з відкриттям Кеплером справжніх законів руху планет навколо Сонця, перший з яких стверджує, що траєкторіями цього руху є не кола, а еліпси, а ще пізніше — з відкриттям нових планет Плутона і Нептуна, — «кубок Кеплера», а разом з ним і правильні многогранники втратили свій колишній ореол таємничості.