Решения типовых задач

№1. Имеются выборочные данные по 15 коммерческим банкам региона:

№ п/п	х	у	№ п/п	х	у	№ п/п	х	у
1 2 3 4 5	15 20 28 38 41	52 86 102 106 124	6 7 8 9 10	42 43 49 52 57	150 140 192 190 240	11 12 13 14 15	58 60 65 72 75	230 220 267 270 315

Построить однофакторную регрессионную линейную модель.

Решение: Предположим, что между объемом собственных средств и привлеченных средств существует линейная корреляционная связь, которую можно выразить уравнением прямой вида .

Для определения параметров и методом наименьших квадратов воспользуемся формулами , .

Таблица 7.7

Расчетные значения, необходимые для исчисления , , , ,

Исходные данные			Расчетные значения
№ банка	Объем собственных средств, млн. руб.	Объем привлеченных средств, млн. руб.
1	2	3	4	5	6
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	15 20 28 38 41 42 43 49 52 57 57 60 65 72 75	52 86 102 106 124 150 140 192 190 240 230 220 267 270 315	-32,6 -27,6 -19,6 -9,6 -6,6 -5,6 -4,6 1,4 4,4 9,4 9,4 12,4 17,4 24,4 27,4	-127 -93 -77 -73 -55 -29 39 13 12 61 51 41 88 91 136	1062,76 761,76 384,16 92,16 43,56 31,36 21,16 1,96 19,36 88,36 88,36 153,76 302,76 595,96 750,76

Продолжение таблицы 7.7

Расчетные значения
7	8	9	10	11	12
16129 8649 5929 5329 3025 841 1521 169 144 3721 2601 1681 7744 8281 18496	4140,2 2566,8 1509,2 700,8 363,0 162,4 179,4 18,2 52,8 573,4 479,4 508,4 1531,2 2220,4 3726,4	40 61 95 138 151 155 159 186 198 219 219 232 253 283 296	12 25 7 -32 -27 -5 -19 6 -7 21 11 -12 14 -13 19	144 625 49 1024 729 25 361 36 49 441 121 144 196 169 361	0,23 0,29 0,07 0,30 0,22 0,03 0,14 0,03 0,04 0,09 0,05 0,05 0,05 0,05 0,06
84260	18732,0	2685	0	4474	1,70

.

Пользуясь расчетными значениями (см. Табл. 7.7.), подсчитаем параметры для данного уравнения регрессии:

,

.

Следовательно, регрессионная модель объема привлеченных средств по собственным средствам банков для данного примера может быть записана в виде следующего уравнения регрессии:

.

Это уравнение характеризует зависимость среднего объема привлеченных средств банков от собственных средств. Расчетные значения , найденные по данному уравнению, приведены в таблице 7.7, гр. 9.

Если параметры регрессионного уравнения подсчитаны верно, то должно соблюдаться равенство сумм теоретических и эмпирических значений объема привлеченных средств, , а сумма разностей между эмпирическими и теоретическими значениями объема привлеченных средств должна быть равна 0 (гр.10. табл. 7.7).

В нашем уравнении регрессии параметр показывает, что с увеличением объема собственных средств одного банка на 1 млн. руб. объем привлеченных средств возрастает в среднем на 4,26 млн. руб.

Если исследуемые признаки имеют разные единицы измерения, для оценки влияния факторного признака на результативный применяется коэффициент эластичности.

Коэффициент эластичности рассчитывается для каждой точки по формуле:

,

где - первая производная уравнения регрессии.

Он показывает, на сколько процентов изменяется результативный признак при изменении факторного признака на 1%.

Средний коэффициент эластичности определяется для уравнения прямой по формуле:

.

Если зависимость величин результативного признака у от значений факторного признака х имеет форму гиперболической зависимости, то есть характеризуется корреляционным уравнением , то для определения параметров и методом наименьших квадратов находим две частные производные от функции , по и , приравниваем их к нулю, получаем систему нормальных уравнений:

.

Производим замену переменных , получаем следующую систему нормальных уравнений:

.

Параметры уравнения гиперболы можно вычислить по формулам:

Гиперболическая форма корреляционной связи используется при изучении зависимости уровня себестоимости единицы продукции от объема выпуска продукции.

Если зависимость величин результативного признака у от значений факторного признака х характеризуется корреляционным уравнением параболы второй степени , то это параболическая зависимость.

И парабола, и прямая являются частным случаем полинома n-ой степени вида .

Систему уравнений для определения параметров можно найти, приравнивая нулю частные производные от по . Решив систему, определяем параметры корреляционного уравнения.

Проверка адекватности однофакторной регрессионной модели

Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным.

Адекватность регрессионной модели при малой выборе можно оценить F критерием Фишера:

,

где m – число параметров модели;

n - число единиц наблюдения;

- факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака фактора, включенного в модель;

- остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих, неучтенных факторов;

- общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию:

.

Эмпирическое значение критерия сравнивается с критическим (табличным) с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m-1), (n-m).

Если > , то уравнение регрессии признается значимым.

Проведем оценку адекватности регрессионной модели , выражающей зависимость среднего объема привлеченных средств банков от собственных средств, с помощью F критерия Фишера:

;

;

;

.

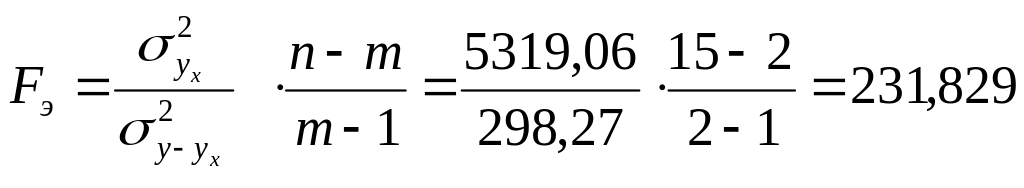Табличное значение F_т с уровнем значимости 0,05 и числом степеней свободы (2-1), (15-2) равно 4,68. (См. Приложение 7). Так как > , то уравнение регрессии можно признать адекватным.

При численности объектов анализа до 30 единиц (при малой выборе) возникает необходимость испытания параметров уравнения на их типичность (значимость). При этом осуществляется проверка, насколько вычисленные параметры характерны для отображаемого комплекса условий, не являются ли полученные значения параметров результатами действия случайных причин.

Для проверки значимости параметров уравнения регрессии используется t – критерий Стьюдента. Вычисляются фактические значения t критерия:

Для параметра :

;

для параметра :

,

где - среднее квадратическое отклонение результативного признака от выравненных значений ;

- среднее квадратическое отклонение факторного признака хот общей средней .

Полученные фактические значения и сравниваются с критическим , который получают по таблице Стьюдента с учетом принятого уровня значимости а (а=0,01 или а=0,05) и числа степеней свободы k=n-2.

Параметр признается значимым (типичным), если эмпирическое значение больше критического табличного :

> < .

Оценим значимость параметров уравнения регрессии с помощью t – критерия Стьюдента:

;

;

;

.

Табличное значение t – критерия с уровнем значимости 0,05 и числом степеней свободы k=n-2=15-2=13 равно 2,161 (Приложение 6).

Сравним фактические значения и с критическим ( =2,161), получаем:

= 4,96 > = 2,161< =15,2.

Следовательно, вычисленные по уравнению регрессии параметры и признаются значимыми.

Измерение тесноты корреляционной связи.

Проверка адекватности регрессионной модели может быть дополнена корреляционным анализом. Для этого необходимо определить тесноту корреляционной связи между переменными х и у.

Теснота связи между двумя признаками может измеряться линейным коэффициентов корреляции (r), корреляционным отношением ( ) и индексом корреляции (R).

Линейный коэффициент корреляции определяется по формулам:

или .

Линейный коэффициент корреляции характеризует степень тесноты только при прямолинейной корреляционной зависимости. С коэффициентом регрессии связан таким соотношением: .

Величина принимает значения в интервале: . Отрицательные значения указывают на обратную связь, положительные – на прямую. При =0 линейная связь отсутствует. Чем ближе по абсолютной величине к единице, тем теснее связь между признаками. И, наконец, при , связь функциональная.

Квадрат линейного коэффициента корреляции называется линейным коэффициентом детерминации, показывает удельный вес влияния данного фактора в общей сумме всех факторов, определяющих уровень результативного признака.

Линейный коэффициент корреляции предложили в конце XIX века английские ученые Ф. Гальтон и К. Пирсон.

При наличии криволинейной корреляционной связи недооценивает тесноту связи и в некоторых случаях может дать неверное представление о степени тесноты связи.

Теоретическое корреляционное отношение ( ) и индекс корреляции ( ) служат для измерения тесноты связи как при прямолинейной, так и при криволинейной корреляционной связи.

Теоретическое корреляционное отношение определяется по формулам:

или .

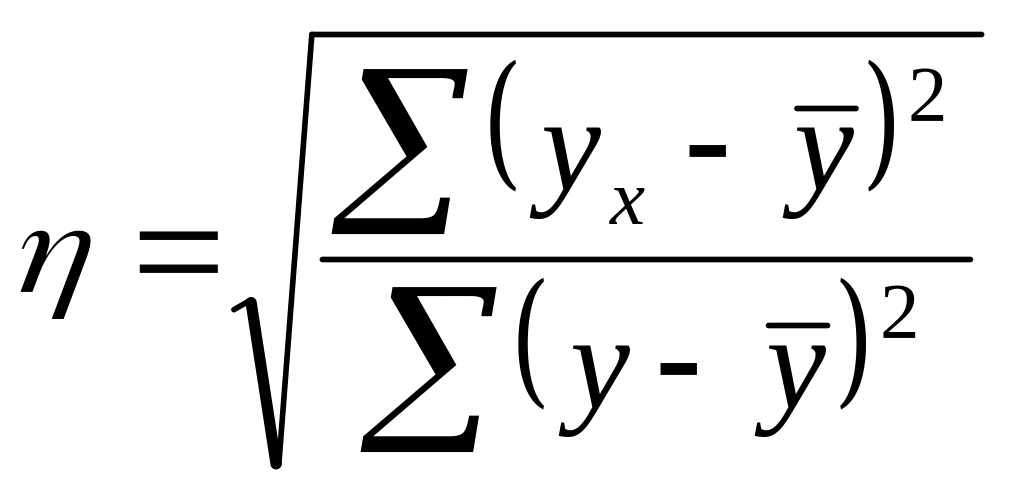Корреляционное отношение в квадрате показывает, какую часть всей вариации результативного признака составляет вариация, вызванная факторным признаком.

Для упрощения расчетов степени тесноты связи часто применяется индекс корреляции. Индекс корреляции определяется по следующим формулам:

или .

Абсолютные размеры линейного коэффициента корреляции, корреляционного отношения, индекса корреляции колеблются от 0 до 1. Направление связи (знак перед и ) определяется непосредственно по исходным данным.

Для качественной оценки тесноты связи можно воспользоваться также шкалой Чеддока:

Величина показателя тесноты связи	Характеристика тесноты
0,1- 0,3 0,3 – 0,5 0,5 – 0,7 0,7 – 0,9 0,9 - 0,99	Слабая Умеренная Заметная Высокая Весьма высокая

Показатели и при прямолинейной связи совпадают. Поэтому вычисленные по одним и тем же данным величины и часто используют для того, чтобы судить о том, насколько для данного случая правильно предположение о наличии именно прямолинейной формы корреляционной связи. Английский статистик Блекман предложил следующий критерий: если разность не превышает 0,1, предположение о прямолинейной форме корреляционной связи можно считать оправданным.

При выборе вида уравнения можно воспользоваться еще критерием криволинейности , если k> 2,5, то предположение о данном виде криволинейной связи можно считать оправданным.

Используем данные табл. 7.7 и рассчитаем линейный коэффициент корреляции, теоретическое корреляционное отношение и индекс корреляции:

;

;

;

;

.

Все показатели тесноты корреляционной связи показывают весьма высокую связь между объемами привлеченных и собственных средств.

Коэффициент детерминации 0,947 означает, что вариация привлеченных средств банков на 94,7% объясняется вариацией собственных средств и на 5,7% - прочими факторами.

Так как , то можно седлать заключение, что гипотеза о линейной форме связи подтверждена.

Проверка значимости показателей тесноты корреляционной связи

Показатели тесноты связи, исчисленные по данным небольшой статистической совокупности, могут искажаться действием случайных причин. Это вызывает необходимость проверки из значимости (надежности, существенности).

Для оценки значимости коэффициента корреляции применяется t–критерий Стьюдента, который определяется по формуле:

,

где - число степеней свободы при данном уровне значимости и объеме выборки n.

Вычисленное по формуле значение сравнивается с критическим .

Если > , то величина коэффициента корреляции признается значимой.

Для оценки значимости индекса корреляции R применяется F -критерий Фишера.

Фактическое значение критерия определяется по формуле:

,

где m– число параметров уравнения регрессии.

Величина сравнивается с критическим , которое определяется по таблице F –критерия с учетом принятого уровня значимости а и числа степеней свободы и .

Если > , то величина индекса корреляции признается значимой. Проверим значимость показателей тесноты корреляционной связи в нашем примере. Значимость линейного коэффициент корреляции оценим с помощью t–критерия:

.

Табличное значение t–критерия с уровнем значимости 0,05 и числом степеней свободы равно 2,161. Фактическое значение =15,2 больше табличного (критического) =2,161, следовательно, коэффициент корреляции можно признать значимым.

Оценка индекса корреляции R=0,973 осуществляется по F–критерию. Определяется фактическое значение:

.

При уровне значимости =0,05 и степенях свободы и табличное значение =4,675. Сравнение =232,3 с =4,675, > позволяет признать индекс корреляции значимым.

Вычислим ошибку аппроксимации по формуле:

.

Так как параметры уравнения регрессии значимы, уравнение значимо, показатели тесноты значимы, ошибка аппроксимации равна 11,3 %, коэффициент детерминации равен 0,947, то построенная регрессионная модель зависимости объема привлеченных средств от объема собственных средств может быть использована для анализа и прогноза.