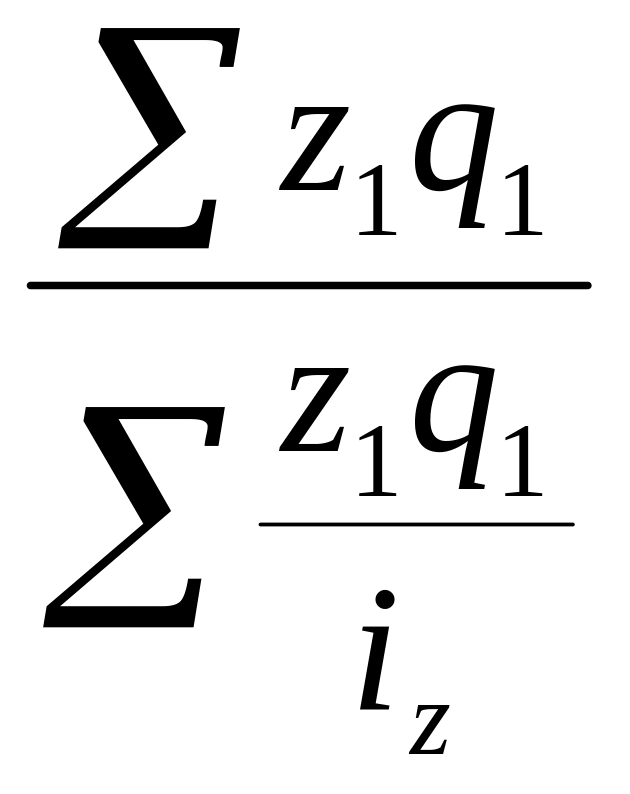4.Средневзвешенные индексы

Средневзвешенные индексы исчисляются тогда, когда имеющаяся в распоряжении информация не позволяет рассчитывать общий агрегатный индекс.

В статистической практике средние индексы рассчитываются преимущественно в форме среднего арифметического и среднего гармонического индексов:

и

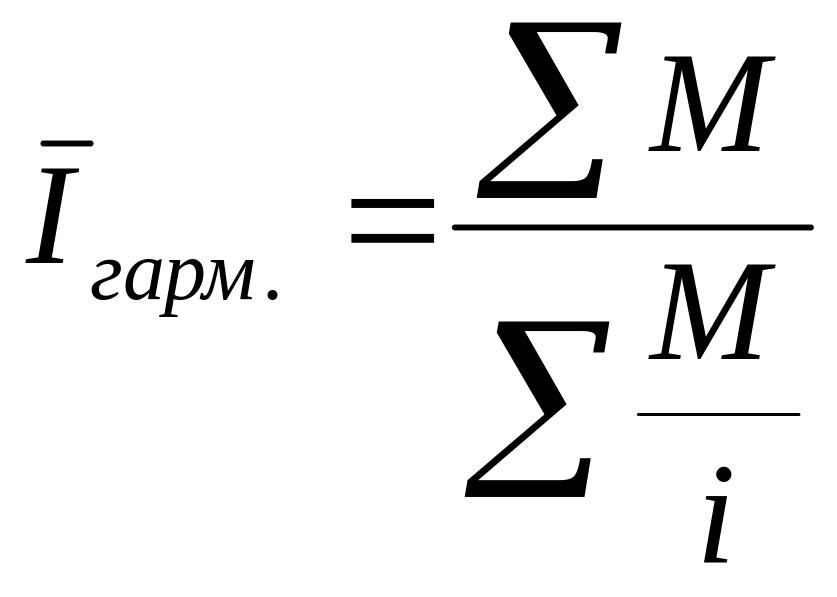
где - индивидуальные индексы изучаемого показателя (индексируемой величины);

- веса соответственно в среднем арифметическом и среднем гармоническом индексах.

Веса для среднего арифметического и среднего гармонического индексов определяются, исходя из тождества их агрегатному, который является основной формой, общего индекса. При этом для каждого конкретного индекса веса особые.

Какой формулой следует воспользоваться в каждом конкретном случае диктуют исходные данные.

Рассмотрим, как производится преобразование агрегатного индекса физического объема в индекс средневзвешенный.

Если располагаем данными об индивидуальных индексах физического объема и стоимости продукции базисного периода в базисных ценах , то знаменатель индекса оставим без изменения, а в числителе агрегатного индекса заменим на . Тогда формула индекса физического объема продукции примет вид .

В таком виде индекс физического объема продукции выступает как средняя арифметическая величина из индивидуальных индексов, взвешенных по стоимости продукции базисного периода в базисных ценах.

Если располагаем данными об индивидуальных индексах физического объема и стоимости продукции отчетного периода в базисных ценах, то числитель агрегатного индекса оставим без изменения, а в знаменателе заменим на . В результате получим общий индекс физического объема в форме среднего взвешенного гармонического индекса

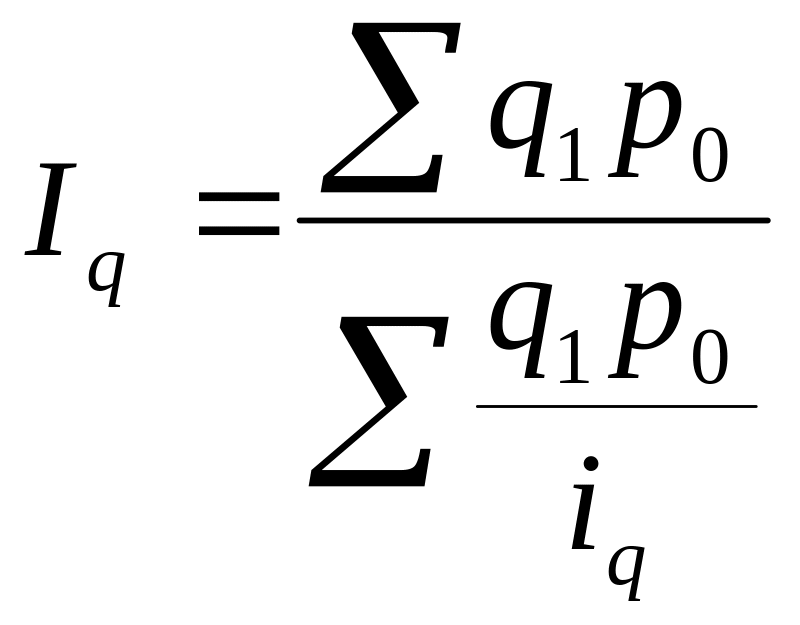
Такое преобразование наглядно показывает тождество между агрегатным индексом и средним арифметическим и средним гармоническим индексами физического объема.

Пример 2.

Имеются следующие данные:

Изделие	Стоимость продукции базисного периода в базисных ценах, тыс. руб.	Индивидуальные индексы объема продукции	Доля изделий в стоимости продукции базисного периода
1	2	3	4
Б В	1000 1600	1,06 1,12	0,385 0,615
Итого	2600	-	1,000

Определить общий индекс физического объема.

Решение.

В данном примере общий индекс физического объема рассчитаем по формуле среднего арифметического индекса

109,7%

Это означает, что в целом по всем изделиям выпуск продукции увеличился в среднем на 9,7% (109,7-100).

Вместо абсолютных данных о стоимости отдельных изделий в базисном периоде можно принимать их доли (удельный вес) в общей стоимости, т.е. .

Тогда формула среднего арифметического индекса из индивидуальных будет иметь вид

поскольку .

Расчет по этой формуле дает тот же результат.

109,7%

Если выражено в процентах формула среднего арифметического индекса будет

Применительно к индексам цен возможны два варианта взвешивания и для среднего арифметического и для среднего гармонического индексов, в зависимости от того по отношению к какому агрегатному индексу рассматривается их тождество: к индексу Ласпейреса или Пааше.

Приведем общую схему преобразования агрегатных индексов в индексы средние арифметические и средние гармонические (Таблица).

Таблица

Схема преобразования агрегатных индексов

Наименование индексов	Индивидуальный индекс	Преобразова ние индивидуаль ного индекса	Агрегатный индекс	Средний арифметический индекс	Средний гармонический индекс
1	2	3	4	5	6
Физического объма
Цен (Пааше)
Цен (Ласпейреса)
Себестоимости
Производительности труда

Рассмотрим пример.

Пример 3. Имеются данные (гр. 1-4)

Товары	Товарооборот, млн. руб.		Изменение цен в отчетном периоде по сравнению с базисным, %	Индивидуальные индексы цены,
	Базисный период,	Отчетный период
1	2	3	4	5
А Б В	110 550 216	120 500 216	Без изменения +5 -20	1,00 1,05 0,80
Итого	876	836

Определить общие индексы цен , товарооборота и физического объема товарооборота .

Решение.

Раз дано изменение цен на товары, значит, известны индивидуальные индексы цен (см. гр.5).

1. Преобразуем агрегатный индекс Пааше. Получим средний

взвешенный гармонический индекс цен, тождественно равный агрегатному индексу. Подсчитаем его.

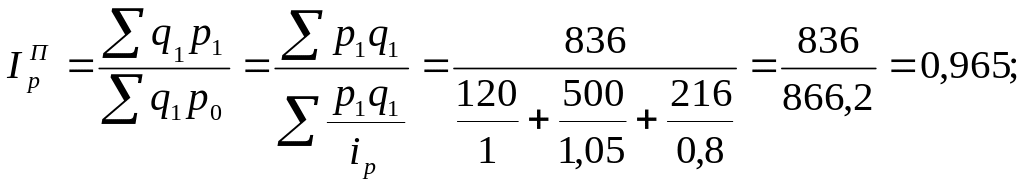96,5%

Следовательно, цены на товары отчетного периода в среднем снизились на 3,5%. Сумма экономии, полученная населением от снижения цен составила

млн. руб.

Индекс цен Ласпейреса преобразуется в средний взвешенный арифметический индекс

98,3%.

Это значит, что цены в отчетном периоде на товары базисного периода в среднем снизились на 1,7% и условное снижение объема товарооборота в связи со снижением цен на товары базисного периода составило

млн. руб.

2. Индекс товарооборота

95,4%

млн. руб., т.е. товарооборот под влиянием 2-х факторов снизился на 4,6% или на 40 млн. руб.

3. Индекс физического объема

98,9%

млн. руб.,

т. е. объем товарооборота снизился в среднем на 1,1% и абсолютное изменение товарооборота под влиянием этого фактора составило 3,8 млн. руб.