Контрольное задание №3 по разделу «Теория вероятностей и математическая статистика» Вариант 5

1. На диаграмме Венна событие изображается…

2. Известны вероятности несовместных событий , , . Указать вероятности событий, которые образуют полную группу

а) , , б) , ,

в) , , г) , ,

3. Внутрь правильного треугольника наудачу брошена точка. Найти вероятность, что точка окажется внутри вписанной окружности.

4. Сколькими способами можно с помощью букв К, А, В, С обозначить вершины четырехугольника?

5. На соревнованиях по легкой атлетике приехала команда из 12 спортсменок. Сколькими способами тренер может определить, кто из них побежит в эстафете 4 по 100 на первом, втором, третьем и четвертом этапах?

6. На плоскости расположены 25 точек так, что три из них не лежат на одной прямой. Сколько существует треугольников с вершинами в этих точках?

7. Каждый из трех стрелков стреляет в мишень по одному разу, причем вероятность попадания в цель для первого стрелка равна 0,9, для второго – 0,8, для третьего – 0,7. Найти вероятность того, что все трое попадут в мишень.

8. В урне 1 белый и 2 черных шара. Извлекают по очереди два шара, причем после первого извлечения шар возвращается в урну. Найти вероятность того, что оба шара белые.

9. В урне 6 белых шаров и 8 черных. Из урны извлекают шары до появления черного шара (без возвращения). Найти вероятность того, что будет проведено всего 3 опыта.

10. Найти вероятность того, что в результате пяти бросков игральной кости нечетное количество очков выпадет не более 2 раз.

11. Событие может наступить лишь при условии появления одного из двух несовместимых событий и , образующих полную группу событий. Известны вероятность и условные вероятности , . Найти вероятность события .

12. На сборку поступило 1000 деталей с первого станка и 3000 – со второго станка. Первый станок дает брака, а второй - брака. Найти вероятность того, что взятая наудачу бракованная деталь окажется с первого станка.

1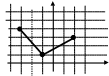 3. Дан графический закон распределения дискретной случайной величины (многоугольник распределения). Записать ряд распределения случайной величины

14. Дискретная случайная величина принимает значения -1, 1, 2 с соответствующими вероятностями 0,2, , 0,3. Найти математическое ожидание случайной величины.

15. Дан ряд распределения случайной величины:

	-4	1	3	5
	0,1	0,3		0,4

Найти моду случайной величины .

16. Дан ряд распределения случайной величины :

	1	4	5	8
	0,3		0,2

Математическое ожидание . Найти вероятность

	1

17. Дан ряд распределения случайной величины :

. Математическое ожидание , дисперсия . Найти вероятность .

18. В урне 2 белых и 3 черных шара. Шары извлекаются из урны без возвращения до появления черного шара. Случайная величина – количество извлеченных белых шаров. Записать ряд распределения случайной величины.

19. Игральную кость бросают 45 раз. Случайная величина – количество выпавших «пятерок» и «шестерок». Найти дисперсию случайной величины.

20. Случайная величина задана функцией распределения

Найти значение параметра .

21. Случайная величина распределена по равномерному закону на отрезке . Найти дисперсию случайной величины.

22. Случайная величина распределена по экспоненциальному закону с параметром . Записать функцию распределения вероятностей случайной величины.

23. Случайная величина распределена по экспоненциальному закону с параметром . Найти среднее квадратичное отклонение случайной величины.

24. Случайная величина распределена по экспоненциальному закону с параметром . Найти вероятность попадания случайной величины в интервал .

25. Закон распределения случайной величины задан функцией плотности . Найти математическое ожидание случайной величины.

26. Функция плотности распределения вероятностей случайной величины имеет вид . В какой точке достигается максимум кривой Гаусса