23.Рациональные корни многочленов с целыми коэффициентами.

Теорема. Если все коэффициенты многочлена: f(x)=a0xn+a1xn-1+a2xn-2+...+an-2x2+an-1x+an являются целыми числами, то всякий целый корень этого многочлена является делителем свободного члена an

Теорема. Если многочлен f(x)=a₀xⁿ+a₁x^n-1+a₂x^n-2+...+a_n-2x²+a_n-1x+a_n с целым коэффициентами и со старшими коэффициентами, равным единице, имеет рациональный корень, то этот корень - целое число

Теорема. Если рациональное число p/q являет корнем многочлена F(x) с целыми коэффициентами, то его свободный член делится на p, а старший коэффициент делится на q.

24.Обобщенная теорема Виета для многочлена n-й степени(без доказательств).

Определение. Функция f(x) действительной или комплексной переменной x называется многочленом, если она может быть представлена в виде:

f(x)=a0xn+a1xn-1+a2xn-2+...+an-2x2+an-1x+an

Где n - любое натуральное число или 0, а a0, a1, ..., an - какие-то действительные числа, называемые коэффициентами многочлена. Утверждение. Любая непрерывная кривая, имеющая на некотором промежутке a ≤ x ≤ b с каждой из прямых, параллельных Oy, в точности одну общую точку, может быть приближенно задана как график функции y= P_n(x), где P_n(x) — многочлен.

Обобщённая теорема Виета.

Пусть х₁; х₂… х_n – корни многочлена

Р(х) = a₀xⁿ + a₁x^n-1 + a_n-1x + a_n тогда

- рациональные корни многочлена

Р(х) = a₀xⁿ + a₁x^n-1 + a_n-1x + a_n с целыми коэффициентами имеют вид x = , где m – делитель свободного члена an, p – делитель старшего коэффициента a0 - приведенный многочлен с целыми коэффициентами (a₀ = 1) не может иметь дробных корней. Целые корни такого многочлена являются делителями его свободного члена.

Геометрия

1. Вектор - это направленный отрезок, соединяющий две точки в пространстве. Расстояние между началом и концом вектора называется его длиной. Для обозначения длины вектора (его абсолютной величины) пользуют символ модуля. Так и обозначают длины соответствующих векторов. Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. Среди коллинеарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы. Векторы называются компланарными, если они лежат, либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости.

Суммой двух векторов и называется вектор, имеющий начало в начале вектора , а конец - в конце вектора , при условии, что вектор приложен к концу вектора .

Для каждого вектора существует противоположный ему вектор такой, что для получения достаточно поменять местами начало и конец вектора. Разностью векторов называется сумма вектора и вектора противоположного вектору.

Произведением вектора на вещественное число (скаляр) называется вектор, такой, что вектор коллинеарен вектору  векторы имеют одинаковое (противоположное) направление.

Угол между векторами — угол между направлениями этих векторов (наименьший угол).

По определению, угол между двумя векторами находится в промежутке [0°; 180°]. Угол между векторами   обозначается так:  .

2. Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат  ,   и  . Оси координат пересекаются в точке  , которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей.   — ось абсцисс,   — ось ординат,   — ось аппликат. Положение точки   в пространстве определяется тремя координатами  ,   и  .

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца.

3. Координаты т. М, т.ч. М₁М=λ∙ММ₂, находятся по следующим формулам:

.

4. Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними. свойства скалярного произведения:

1. свойство коммутативности скалярного произведения  ;

2. свойство дистрибутивности   или  ;

3. сочетательное свойство   или  , где   - произвольное действительное число;

4. скалярный квадрат вектора всегда не отрицателен  , причем  тогда и только тогда, когда вектор   нулевой.

Скалярным произведение двух векторов, заданных своими координатами, равно сумме произведений одноименных координат этих векторов.

По определению скалярное произведение векторов есть  . Если векторы   и   ненулевые, то можно разделить обе части последнего равенства на произведение длин векторов   и  , и мы получим формулу для нахождения косинуса угла между ненулевыми векторами:  .

Для перпендикулярности двух ненулевых векторов   и   необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство

Билет 5.

Билет 6.

Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости.

Билет 7

Пусть в трехмерном пространстве задана прямоугольная система координат Oxyz.

В прямоугольной системе координат Oxyz в трехмерном пространстве уравнение вида  , где a, b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках.

Билет 8

Угол между двумя пересекающимися по прямой c плоскостями   и   – это угол между двумя пересекающимися прямыми a и b, по которым плоскости   и  пересекаются с плоскостью  , перпендикулярной к прямой c.

cos α= |A₁·A₂ + B₁·B₂ + C₁·C₂|/(A₁² + B₁² + C₁²)^1/2(A₂² + B₂² + C₂²)^1/2

9 билет

10 билет

11.Уравнение прямой, проходящей через две точки: A(x₁, y₁) и B(x₂, y₂), записывается так:

(2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

(3)

14.  Для того, чтобы прямая и плоскость были параллельны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были перпендикулярны. Для этого необходимо, чтобы их скалярное произведение было равно нулю.

15. Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были коллинеарны. Это условие выполняется, если векторное произведение этих векторов было равно нулю.

16. Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость.

Если известны прямоугольные декартовы координаты направляющего вектора прямой и нормального вектора плоскости a = (a₁; a₂; a₃) и n = (А; В; С), то угол φ может быть вычислен с помощью формулы

или

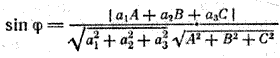(1)

18. Определение расстояния между точкой и плоскостью.

Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость.

Поэтому решение этой задачи состоит из последовательного выполнения следующих графических операций:

1) из точки А опускаем перпендикуляра на плоскость а (рис.269);

2) находим точку М пересечения этого перпендикуляра с плоскостью М «= а П а;

3) определяем длину отрезка

• составляем уравнение прямой a, которая проходит через точку М₁ и перпендикулярна к плоскости  ;

• находим координаты   точки H₁ - точки пересечения прямой a и плоскости  ;

• вычисляем расстояние от точки М₁ до плоскости   по формуле 

19. Пусть центр сферы находится в точке A (a; b; c), а радиус сферы равен R. Точками сферы являются те и только те точки пространства, расстояние от которых до точкиA равно R. Квадрат расстояния от любой точки B (x; y; z) сферы до точки A равен

(x – a)² + (y – b)² + (z – c)².

Поэтому уравнение сферы с центром A (a; b; c) и радиусом R имеет вид:

(x – a)² + (y – b)² + (z – c)² = R².