13.Общая характеристика языков программирования

Языки программирования — искусственные языки. От естественных они отличаются ограниченным числом «слов», значение которых понятно транслятору, и очень строгими правилами записи команд {операторов). Совокупность подобных требований образует синтаксис языка программирования, а смысл каждой команды и других конструкций языка — его семантику. Нарушение формы записи программы приводит к тому, что транслятор не может понять назначение оператора и выдает сообщение о синтаксической ошибке, а правильно написанное, но не отвечающее алгоритму использование команд языка приводит к семантическим ошибкам (называемым еще логическими ошибками или ошибками времени выполнения). Процесс поиска ошибок в программе называется тестированием, процесс устранения

ошибок — отладкой.

Pascal (Паскаль). Язык.Паскаль, созданный в конце 70-х годов основоположником множества идей современного программирования Никлаусом Виртом, во многом напоминает Алгол, но в нем ужесточен ряд требований к структуре программы и имеются возможности, позволяющие успешно применять его при создании крупных

проектов.

Basic (Бейсик). Для этого языка имеются и компиляторы, и интерпретаторы, а по популярности он занимает первое место в мире. Он создавался в 60-х годах в качестве учебного языка и очень прост в изучении.

С (Си). Данный язык был создан в лаборатории Bell и первоначально не рассматривался как массовый. Он планировался для замены ассемблера, чтобы иметь возможность создавать столь же эффективные и компактные программы и в то же время не зависеть от конкретного типа процессора.

15. Характеристика операционных систем семейства Windows.

Примером новых ОС является система Microsoft Windows NT, являющаяся быстродействующей 32-разрядной сетевой системой с графическим интерфейсом и встроенными сетевыми средствами. Данная ОС ориентирована на работу в сети.

Для того чтобы осуществить связи между удаленными объектами с помощью сервиса удаленного доступа, требуются модемы на обоих концах соединения, принтеры, накопители на магнитных лентах и другие устройства.

Операционная система Wndows NT обладает свойствами, перечисленными далее.

1. Переносимость, т. е. способность работать на CISC– и RISC-процессорах.

2. Многозадачность, т. е. возможность использования одного процессора для работы нескольких приложений или потоков нитей.

3. Многопроцессорная обработка, включающая в себя несколько процессоров, способных одновременно выполнять множество нитей, по одной на каждый находящийся в компьютере процессор.

4. Масштабируемость, т. е. возможность автоматического использования положительных качеств добавленных процессоров. Например, для ускорения работы приложения ОС может автоматически подключать дополнительные одинаковые процессоры. Масштабируемость Windows NT обеспечивается:

• многопроцессорностью локальных компьютеров, т. е. наличием у них нескольких процессоров, взаимодействие между которыми происходит через разделяемую память;

• симметричной многопроцессорной обработкой, предполагающей одновременное выполнение приложений на нескольких процессорах;

• распределенной обработкой информации между несколькими объединенными в сеть компьютерами, реализующейся на основе концепции вызова удаленных процедур, которая поддерживает архитектуру клиент-сервер.

5. Архитектура клиент-сервер, осуществляющая присоединение однопользовательской рабочей станции и многопользовательских серверов общего назначения (для распределения между ними нагрузки по обработке данных). Данное взаимодействие имеет объектную ориентацию; при этом объект, отправляющий сообщение, является клиентом, а объект, получающий сообщение, – сервером.

6. Объектная архитектура. Объектами являются объекты каталога, процесса и нитей управления, объекты раздела и сегмента памяти, объекты порта. Тип объекта включает в себя тип данных, набор атрибутов и список операций, которые могут выполняться над ним. Управление объектами можно производить с помощью процессов ОС, т. е. посредством некоторой последовательности действий, определяющих соответствующую программу и составляющих задачу.

7. Расширяемость, которая обусловлена открытой модульной архитектурой, позволяющей добавлять новые модули на все уровни ОС. Модульная архитектура способствует соединению с другими сетевыми продуктами, а компьютеры, функционирующие под управлением Windows NT, способны взаимодействовать с серверами и клиентами других ОС.

8. Надежность и отказоустойчивость, определяемые тем, что архитектура защищает ОС и приложения от разрушения.

9. Совместимость, т. е. возможность Windows NT версии 4 поддерживать приложения MS DOS, Windows 3.x, OS/2 и иметь при этом широкий набор устройств и сетей.

10. Доменная архитектура сетей, предопределяющая группировку компьютеров в домены.

11. Многоуровневая система безопасности, которая была создана для обеспечения безопасности ОС, приложений, информации от разрушения, незаконного доступа, непрофессиональных действий пользователя. Она работает на уровне пользователя, локальных и сетевых компьютеров, доменов, объектов, ресурсов, сетевой передачи информации, приложений и т. д.

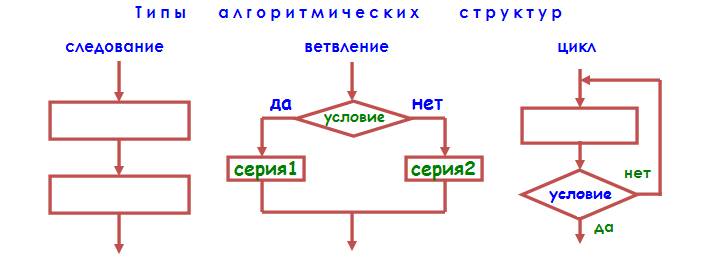
16. Способы записи алгоритма. Графические схемы алгоритмов.

Первый способ записи алгоритмов – словесный, на естественном языке.

Второй способ записи алгоритмов – составление блок-схем. Он очень распространен, в силу его удобства и понятности.

Блок-схема – это графическое изображение алгоритма в виде определенным образом связанных между собой нескольких типов блоков.

 

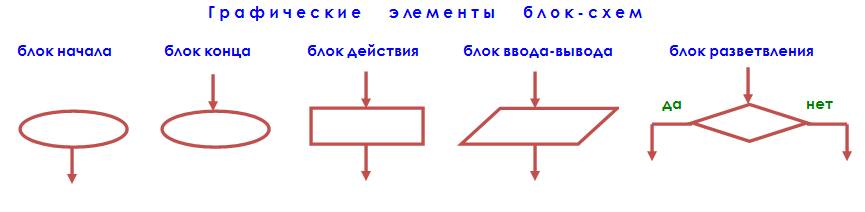
Перечислим графические элементы блок-схем. Это:

         блок начала;

         блок конца;

         блок ввода – вывода;

         блок действия;

         блок разветвления.

 

Язык схем настолько четок, что исполнитель, получивший блок-схему алгоритма, ни в каких дополнительных разъяснениях не нуждается.

При составлении блок-схем следует руководствоваться простыми правилами:

Блок-схема должна развиваться сверху вниз; при необходимости – слева направо.

Каждый участок блок-схемы линейного алгоритма должен иметь один вход и один выход; в случае ветвления алгоритма может быть два выхода.

В линейном алгоритме выход рисуется точно под входом.

Если не требуется проверять выполнение каких-либо условий, то последовательность выполняемых действий всегда одинакова. Такие алгоритмы называют линейными.

 

Алгоритм любой задачи можно описать, используя три типа управляющих структур:

         Следование;

         Ветвление;

         Цикл.

 

 

Кроме естественного языка и языка блок-схем, существует еще один способ записи алгоритма – это запись на языке программирования.

 

Итак, существует три способа записи алгоритмов:

         словесный, на естественном языке;

         на языке блок-схем;

         на языке программирования.

. Графические схемы алгоритмов

Графическая схема алгоритма состоит из отдельных блоков, связанных линиями потоков. Каждый блок описывает конкретный шаг алгоритма. Блоки делятся на:

начало или конец алгоритма

ввод или вывод данных

выполнение операции или действия

проверка условия

17. Линейные и разветвляющиеся алгоритмы. Примеры схем алгоритмов.

Линейный алгоритм - это такой, в котором все операции выполняются последовательно одна за другой (рис. 1.6).

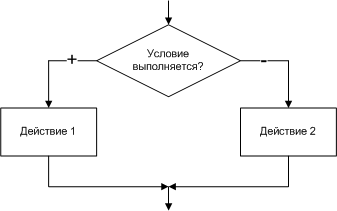
Алгоритмы разветвленной структуры применяются, когда в зависимости от некоторого условия необходимо выполнить либо одно, либо другое действие. В блок-схемах разветвленные алгоритмы изображаются так, как показано на рис. 1.10 - 1.11.

Рис. 1.10 Фрагмент алгоритма	Рис. 1.11 Пример разветвления

18. Циклические алгоритмы. Примеры схем алгоритмов.

Алгоритмы циклической структуры

Циклом называют повторение одних и тех же действий (шагов).

Последовательность действий, которые повторяются в цикле, называют телом

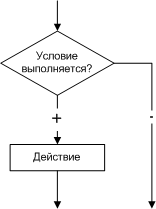
цикла. Существует несколько типов алгоритмов циклической структуры. На рис.

5.1 изображен цикл с предусловием, а на рис. 5.2 – цикл с постусловием, которые

называют условными циклическими алгоритмами. Нетрудно заметить, что эти

циклы взаимозаменяемы и обладают некоторыми отличиями.

в цикле с предусловием условие проверяется до тела цикла, в цикле с

постусловием – после тела цикла;

в цикле с постусловием тело цикла выполняется хотя бы один раз, в цикле с

предусловием тело цикла может не выполниться ни разу;

в цикле с предусловием проверяется условие продолжения цикла, в цикле с

постусловием – условие выхода из цикла.

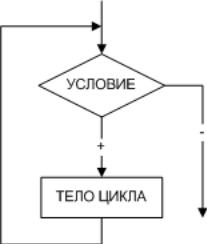
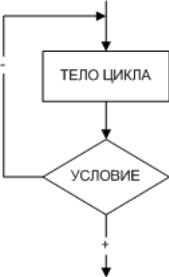
Рис. 5.1. Алгоритм циклической Рис. 5.2. Алгоритм циклической

структуры с предусловием структуры с постусловием

При написании условных циклических алгоритмов следует помнить

следующее. Во-первых, чтобы цикл имел шанс когда-нибудь закончиться,

содержимое его тела должно обязательно влиять на условие цикла. Во-вторых,

условие должно состоять из корректных выражений и значений, определенных

еще до первого выполнения тела цикла.

Кроме того, существует так называемый безусловный циклический алгоритм

(рис. 5.3), который удобно использовать, если известно, сколько раз необходимо

выполнить тело цикла.

Выполнение безусловного циклического алгоритма начинается с присвоения

переменной i стартового значения in. Затем следует проверка, не превосходит ли

переменная i конечное значение iк. Если превосходит, то цикл считается

завершенным, и управление передается следующему за телом цикла оператору. В

противном случае выполняется тело цикла, и переменная i меняет свое значение в

соответствии с указанным шагом di. Далее, снова производится проверка

значения переменной i и алгоритм повторяется. Понятно, что безусловный

циклический алгоритм можно заменить любым условным. Например, так как

показано на рис. 5.4.

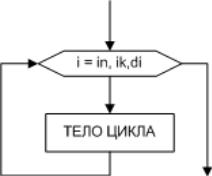
Рис. 5.3. Алгоритм циклической структуры без условия

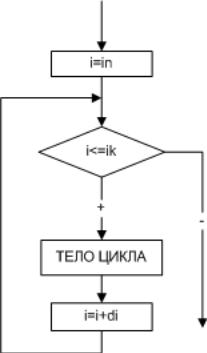
Рис. 5.4. Условный циклический алгоритм с известным числом повторений

Отметим, что переменную i называют параметром цикла, так как это

переменная, которая изменяется внутри цикла по определенному закону и влияет

на его окончание

19. Применение циклов в алгоритмах обработки массивов: ввод-вывод одномерных массивов.

Ввод-вывод элементов одномерного массива

При вводе массива необходимо последовательно вводить 1-й, 2-й, 3-й и т.д.

элементы массива, аналогичным образом поступить и при выводе. Следовательно,

необходимо организовать цикл.

Блок-схемы алгоритмов ввода элементов массива изображены на рис. 6.3-6.4

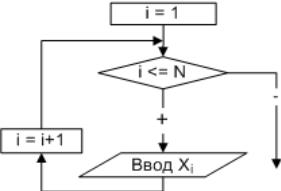
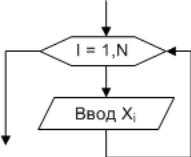
Рис 6.3 Алгоритм ввода массива Рис. 6.4. Алгоритм ввода массива

с использованием цикла с использованием

с предусловием безусловного цикла

Как видно, безусловный цикл удобно использовать для обработки всего

массива, и в дальнейшем при выполнении таких операций будем применять

именно его. Вывод массива организуется аналогично вводу.

Рассмотрим несколько примеров обработки массивов. Алгоритмы, с

помощью которых обрабатывают одномерные массивы, похожи на обработку

последовательностей (вычисление суммы, произведения, поиск элементов по

определенному признаку, выборки и т. д.). Отличие заключается в том, что в

массиве одновременно доступны все его компоненты, поэтому становится

возможной, например, сортировка его элементов и другие, более сложные

преобразования.

20. Применение циклов в алгоритмах обработки массивов: нахождение суммы и произведения элементов одномерного массива.

Вычисление суммы элементов массива

Дан массив X, состоящий из n элементов. Найти сумму элементов этого массива.

Процесс накапливания суммы элементов массива достаточно прост и практически

ничем не отличается от суммирования значений некоторой числовой

последовательности. Переменной S присваивается значение равное нулю, затем

последовательно суммируются элементы массива X. Блок-схема алгоритма

расчета суммы приведена на рис. 6.5.

Вычисление произведения элементов массива

Дан массив X, состоящий из n элементов. Найти произведение элементов этого

массива. Решение этой задачи сводится к тому, что значение переменной Р, в

которую предварительно была записана единица, последовательно умножается на

значение i–го элемента массива. Блок-схема алгоритма приведена на рис. 6.6.

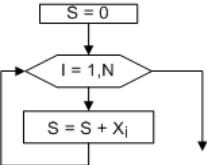
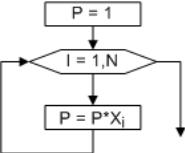
Рис. 6.5. Алгоритм вычисления Рис. 6.6. Вычисление произведения

суммы элементов массива элементов массива

21. Применение циклов в алгоритмах обработки массивов: нахождение минимального (максимального) элемента одномерного массива и его порядкового номера.

Поиска максимального элемента в массиве и его номера

Дан массив X, состоящий из n элементов. Найти максимальный элемент массива и

номер, под которым он хранится в массиве.

Алгоритм решения задачи следующий. Пусть в переменной с именем Max

хранится значение максимального элемента массива, а в переменной с именем

Nmax – его номер. Предположим, что первый элемент массива является

максимальным, и запишем его в переменную Max, а в Nmax занесем его номер,

то есть – 1. Затем все элементы, начиная со второго, сравниваем в цикле с

максимальным. Если текущий элемент массива оказывается больше

максимального, то записываем его в переменную Max, а в переменную Nmax –

текущее значение индекса i. Процесс определения максимального элемента в

массиве приведен в таблице 6.1 и изображен при помощи блок-схемы на рис. 6.7.

Таблица 6.1. Определение максимального элемента и его номера в массиве

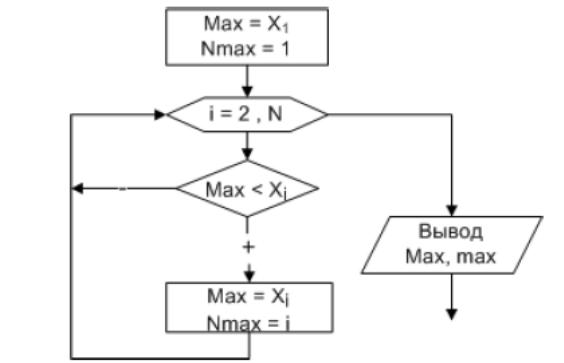
Рис. 6.7. Поиск максимального элемента и его номера в массиве

Совет. Алгоритм поиска минимального элемента в массиве будет отличаться

от приведенного выше лишь тем, что в условном блоке знак поменяется с > на <.

22. Алгоритмы обработки одномерных массивов: нахождение суммы и произведения, удовлетворяющих заданным условиям. Примеры.

23. Алгоритм ввод-вывода элементов двумерных массивов.

Алгоритмы обработки матриц

Матрица– это двумерный массив, каждый элемент которого имеет два индекса:

номер строки – i; номер столбца – j. Поэтому для работы с элементами матрицы

необходимо использовать два цикла. Если значениями параметра первого цикла

будут номера строк матрицы, то значениями параметра второго – столбцы (или

наоборот). Обработка матрицы заключается в том, что вначале поочередно

рассматриваются элементы первой строки (столбца), затем второй и т.д. до

последней. Рассмотрим основные операции, выполняемые над матрицами при

решении задач.