Лабороторна робота №5

Завдання: Побудувати дерево рекурсії, як графічне представлення породжуваного алгоритмом, ,ланцюга рекурсивних викликів.

Теоретичні відомості:

Під рекурсією розуміють метод визначення функції через її попередні і раніше визначені значення, а також спосіб організації обчислень, при якому функція викликає сама себе з іншим аргументом.

Більшість сучасних мов високого рівня підтримують механізм рекурсивного виклику, коли функція, як елемент структури мови програмування, повертаюча обчислене значення по своєму імені, може викликати сама себе з іншим аргументом. Ця можливість дає змогу напряму реалізовувати обчислення рекурсивно визначених функцій. Відмітимо, що в силу тезису Черча–Тьюринга апарат рекурсивних функцій Черча рывний машині Тьюринга, і, з цього виливає, що будь-який рекурсивний алгоритм може бути реалізований ітераціоно.

F(n); If n=0 or n=1 (перевірка можливості прямого обчислення) Then F <-- 1 Else F <-- n*F(n-1); ( рекурсивний виклик функції) Return (F); End;

Аналіз трудомісткості рекурсивних реалізацій алгоритмів, очевидно, зв’язаний як з кількістю операцій, виконуваних при одному виклику функції, так і з кількістю таких викликів. Графічне представлення даним алгоритмом ланцюга рекурсивних викликів називається деревом рекурсивних викликів. Більш детальний розгляд призводить до необхідності урахування затрат як на організацію викликів функції і передачі параметрів, так і на повернення обчислених значень і передачу управління в точку виклику.

Можно заметить, що де-яка гілка дерева рекурсивних викликів обривається при досягнені такого значення передаваного параметра, при якому функція може бути обчислена безпосередньо. Таким чином, рекурсія еквівалентна конструкції циклу, в якому кожний прохід є виконання рекурсивної функції з заданим параметром.

Розглянемо приклад для функції обчислення факторіала (рис. 1):

Ланцюг рекурсивних повернень

Ланцюг рекурсивних викликів

Рис. 1 Дерево рекурсії при обчислені факторіала – F(5)

Дерево рекурсивних викликів може мати і більш складну структуру, якщо при кожному виклику породжується декілька звернень.

Пояснення до завдання:

Треба по заданій формулі написати програму з використанням рекурсивних функцій, та окремо від програми намалювати дерево рекурсивних викликів.

Код програми:

program Rekursia;

uses crt;

Function Rec( i:integer) :Real; //рекурсия сумы

{-------}

Function Rec1( j:integer):real; //рекурсия умножения

begin

if not(j=1) then rec1:=rec1(j-1)*(2+1/j)

else rec1:=2+1/j;

end;

{--------}

begin

if not(i=3) then begin rec:=rec(i-1)+(2*sqr(i)/rec1(i)); end

else begin rec:=(2*sqr(i)/rec1(i)) ; end;

end;

begin

writeln('rec= ',rec(8));

end.

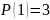
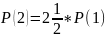
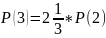
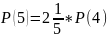
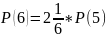
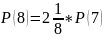
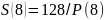
8

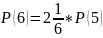
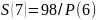
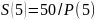
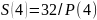
7

6

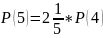
S=S(3)+S(4)+S(5)+S(6)+S(7)+S(8)

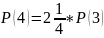
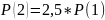
4

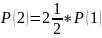
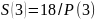
3

Пояснення до виконаного завдання:

Все що робить програма, це виводить результат обрахунку заданої функції підрахованої за допомогою рекурсії. Також окремо від програми бцло складено дерево рекурсії, яке наглядно показує, глубину виконання рекурсії.