Лабороторна робота №4

Завдання:

Провести поопераційний часовий аналіз алгоритму, використаного в лабораторній роботі №3.

Ввести параметри p і q, які встановлюють співвідношення між часом виконання операції множення, додавання і присвоєння для операндів дійсного типу.

t_* = q ∙ t₊, q > 1;

t_← = r ∙ t₊, r < 1;

Пояснення до завдання:

Програма повинна формувати масив за заданою формулою та виводити результат на екран. На основі створеного алгоритму для виконання програми, окремо провести поопераційний аналіз алгоритму. Як провести поопераційний часовий аналіз можна дізнатися в Теоретичних відомостях.

Теоретичні відомості:

Порівняння двух алгоритмів по їх функції трудомісткості вносить деяку помилку в резульиаим, які ми отримуємо. Основною причиною цієї помилки є різна частотна зустрічаємість елементарних операцій, породжувана різними алгоритмами і відмінність в часах виконання елементарних операцій на реальному процесорі. Таким чином, виникає задача переходу від функції трудомісткості до оцінки часу роботи алгоритму на конкретному процесорі:

Дано: F_A(D_A) - трудомісткість алгоритму, потрібно визначити час роботи програмної реалізації алгоритму – T_A(D_A).

На шляху побудови часових оцінок ми стикаємось з цілим набором різних проблем, пофакторний облік яких викликає істотні трудності. Вкажемо основні з цих проблем:

• неадекватність формальної системи запису алгоритму і реальної системи команд процесора;

• наявність архітектурних особливостей суттєво впливающих на час виконання програми, таких як конвеєр, кешування пам'яті, предвибірка команд і даних, і т.д.;

• різний час виконання реальних машинних команд;

• відмінність в часі виконання однієї команди, в залежності від значення операндів

• відмінність часу реального виконання однорідних команд в залежності від типів даних;

• неоднозначність компіляції вихідного тексту, обумовлена як самим компілятором, так і його налаштуваннями.

Спроби різного підходу до обліку цих факторів привели до появи різних методик переходу до часових оцінок.

1) Поопераційний аналіз

Ідея поопераційного аналізу полягає в отриманні поопераційної функції трудомісткості для кожної з використовуваних алгоритмом елементарних операцій з урахуванням типів даних. Наступним кроком є експериментальне визначення середнього часу виконання даної елементарної операції на конкретній обчислювальній машині. Очікуваний час виконання розраховується як сума добутків поопераційної трудомісткості на середній час операцій:

T_A(N) = å F_aопi(N) * `t _опi

2) Метод Гіббсона

Метод передбачає проведення сукупного аналізу по трудомісткості і перехід до часових оцінок на основі приналежності розв'язуваної задачі до одного із наступних типів:

• задачі научно-технічного характеру з перевагою операцій з операндами дійсного типу;

• задачі дискретної математики з перевагою операцій з операндами цілого типу

• задачі баз даних с перевагою операцій з операндами строкового типа

Далі на основі аналізу множини реальних програм для рішення відповідних типів задач визначається частотна зустрічальність операцій (рис 5.1), створюються відповідні тестові програми, і визначається середній час на операцію в даному типі задач –`t _{тип задачи}.

Рис 5.1 Можливий вид частотної зустрічальності операцій

На основі отриманої інформації оцінюється загальний час роботи алгоритму у вигляді:

T_A(N) = F_A(N) *`t _{тип задачи}

3) Метод прямого визначення середнього часу

В цьому методі також проводиться сукупний аналіз по трудомісткості – визначається F_A(N), після чого на основі прямого експерименту для різних значень N_э визначається середній час роботи даної програми T_э і на основі відомої функції трудомісткості розраховується середній час на загальну елементарну операцію, породжене даним алгоритмом, компілятором і комп'ютером – `t_а. Ці дані можуть бути (в речені про стійкість середнього часу по N) інтерполірованы чи экстраполіровані на інші значення розмірності задачі наступним чином:

`t<sub>а</sub>= T<sub>э</sub>(N<sub>э</sub>) / F<sub>A</sub>(N<sub>э</sub>), T(N) = `t_а * F_A(N).

Код програми:

program Lexus;

uses crt;

const x=-3.41; c1=0.2;c2=0.3;c3=0.2;c4=0.3;M=2;

type mas=array[1..7] of real;

var R:mas; i:integer;y,Sd,Fa:real;

begin

y:=32.2;

for i:=1 to 7 do begin

R[i]:=(sqrt(abs(sin(x*y)+cos(x*y)))+sqrt(abs(sin(x)+cos(x))))/(sqrt(abs(sin(y)+cos(y)))+2.1);

writeln('R[',i,']= ',R[i]);

y:=y+0.2;

end;

writeln;

t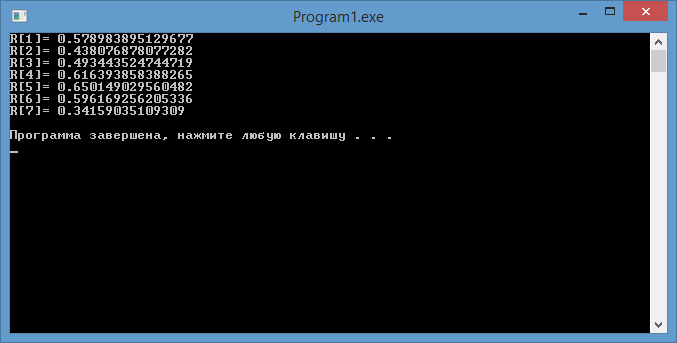 ₊=1,5; N₊=5;

t₌=1; r=2/3; N₌=1;

t_*=2; q=4/3; N_*=2;

t_/=2; N_/=1;

t_cos=5; N_cos=3;

t_sin=5; N_sin=3;

t_√=3; N_√=3;

T=t₊*N₊ + t₊*r*N₌ + t₊*q*N_* +t_/*N_/ + t_cos*N_cos + t_sin*N_sin + t_√*N_√=

6,5+1+4+2+15+15+9=56,5;

Пояснення до виконаного завдання:

Програма формує масив на основі заданої умови. Та виводить сформований масив на екран. Також на основі створеного алгоритму був проведений поопераційний часовий аналіз, результат якого становить 56,5 тактів.