§ 4. Теоремы сложения и умножения. Условная вероятность
Справедливы следующие теоремы:
Теорема сложения вероятностей несовместных событий.
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
.
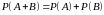Теорема умножения вероятностей независимых событий.
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
.
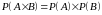Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления двух событий равна произведению одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
.
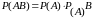Теорема
2 является частным случаем теоремы 3,
так как для независимых событий
-
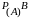вероятность события В при условии
наступления события А, то есть условная
вероятность, равна безусловной вероятности
.
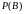4 Теорема сложения вероятностей совместных событий:
Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
.
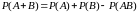Теоремы верны не только для двух событий, но и для большого числа.
1. Зачёт по стрельбе сдан, если у курсанта оценка не ниже 4. Найти вероятность сдачи зачёта, если известно, что он получит 5 с вероятностью 0,3 и 4 – с вероятностью 0,5.
2. В электрическую цепь включены последовательно 2 предохранителя. Вероятность выхода из строя первого равна 0,6; второго – 0,2. Найти вероятность прекращения питания в результате выхода из строя хотя бы одного из них. (0,68)
3. Из полной колоды карт (52 карты) вынимают наугад 3 карты (без возвращения). Вычислить вероятность, что среди вынутых карт 1) точно 1 туз; 2) хотя бы 1 туз. (0,204; 0,98)
4. Два стрелка независимо друг от друга стреляют в одну цель по одному разу. Вероятность попадания в цель первого стрелка – 0,9, второго – 0,8. Найти вероятность поражения цели по крайней мере одним стрелком. (0,98)
5. Два стрелка независимо друг от друга стреляют в одну цель по одному разу. Вероятность попадания в цель первого стрелка – 0,6, второго – 0,7. Найти вероятность того, что оба стрелка попадут в цель.
6. Рабочий обслуживает 3 станка, ремонтируя остановившиеся станки. Вероятность, что первый станок не остановится в течение часа равна 0,9; второй – 0,8; третий – 0,7. Найти вероятность того, что в течение часа рабочему не придётся подходить к станкам и ремонтировать их. (0,504)
7. Из партии изделий ОТК проверяет половину и признаёт годной всю партию, если среди проверенных изделий не более одного бракованного. Найти вероятность того, что партия из 20 изделий, в которой 2 бракованные, будет признана годной. (29/38)
8. В лотерее на серию 1000 билетов приходится 120 денежных и 80 вещевых выигрышей. Найти вероятность выигрыша на один билет. (0,2)
9. Каждое из четырёх несовместных событий может произойти с вероятностями соответственно 0,01; 0,02; 0,03 и 0,04. Найти вероятность того, что в результате опыта произойдёт хотя бы одно из этих событий. (0,1)
10. Найти вероятность извлечь из колоды (52 карты) фигуру любой масти или карту пиковой масти (фигурой называется валет, дама или король). (11/26)
11. В урне 10 белых, 20 чёрных и 30 синих шаров. Случайным образом достают 3 шара. Найти вероятность того, что все шары синие. (0,1186)
12. В урне находятся 5 белых и 20 чёрных шаров. Из урны последовательно вынимают шары до тех пор, пока не будет вынут белый шар. Найти вероятность того, что при этих условиях будет произведено 3 вынимания, т.е. что до первого белого шара будет вынуто 2 чёрных шара. (0,138)
13. На разных карточках разрезной азбуки написано 32 буквы русского алфавита. % карточек вынимают наугад одна за другой и укладывают на стол в порядке появления. Найти вероятность того, что получится слово «финал».
13. Из полной колоды карт (52 карты) вынимают сразу 4 карты. Найти вероятность того, что все эти 4 карты будут разных мастей. (0,106)
14. Одновременно бросили 4 игральных кубика. Найти вероятность того, что хотя бы на одном из них выпадет пятёрка. (0,5177)
15. Предприятие изготавливает 97% стандартных микросхем, из которых 90% потом сертифицируется. Найти вероятность того, что взятая наудачу микросхема, изготовленная на этом предприятии, окажется сертифицированной. (0,873)
16. Два торпедных катера одновременно выпустили по одной торпеде по цели. Вероятность попадания в цель у первого катера 0,6, у второго – 0,5. Найти вероятность того, что: а) обе торпеды попадут в цель; б) хотя бы одна торпеда попадёт в цель. (0,3; 0,8)
17. Три орудия произвели залп по цели. Вероятность попадания в цель при одном выстреле из орудия такова: для первого – 0,8; для второго – 0,6; для третьего – 0,9. Найти вероятность того, что: а) только один снаряд попадёт в цель; б) только два снаряда попадут в цель; в) все три снаряда попадут в цель. (0,116; 0,444; 0,432)
Д/з 18. Гидрологический зонд состоит из четырёх основных элементов: блока измерения давления, блока измерения температуры, блока измерения электропроводности и блока кодировки и передачи информации. Неисправность любого из блоков приводит к невозможности получения необходимых данных. Вероятности выхода из строя блоков в течение месяца равны и составляют 0,02. Найти вероятность того, что во время рейса длительность 1 месяц зонд выйдет из строя. (0,076)
Д/з 19. В урне находятся 7 белых, 13 чёрных, 10 зелёных и 3 красных шара. Случайным образом из урны достают 3 шара. Найти вероятность того, что все они одного цвета. (0,081)
Д/з 20. Вероятность события А появится хотя бы 1 раз при двух независимых испытаниях равна 0,75. Найти вероятность появления события в одном испытании (предполагается, что вероятность появления события в обоих испытаниях одна и та же). (0,5)
Д/з 21. Зависимы или независимы: а) несовместные события; б) события образующие полную группу; с) равновозможные события. (зав.; зав.; и незав. и незав.)