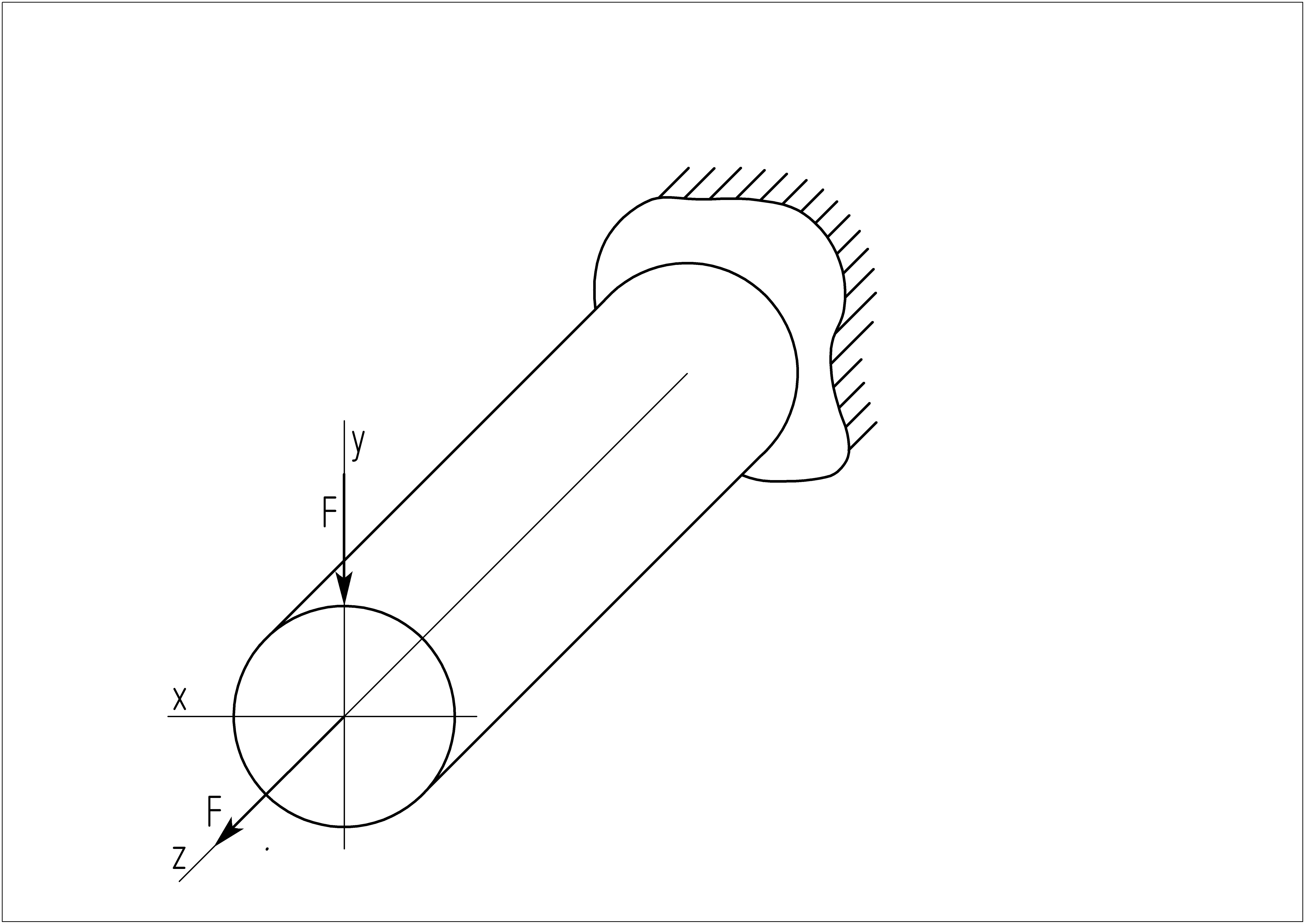
3.1.2. Случай прямого изгиба с растяжением-сжатием

Что такое прямой изгиб с растяжением-сжатием?

Совокупность прямого изгиба, при котором силовая линия совпадает с одной из главных центральных осей сечения, с одновременным силовым воздействием в направлении продольной оси элемента конструкции приводит к данному случаю деформации. Например:

Чтобы научиться оценивать прочность

в случае прямого изгиба с растяжением-сжатием надо знать!

1. Что по сути это частный случай косого изгиба с растяжением-сжатием. Т.к., если косой изгиб представляют как два прямых, то в данном случае присутствует один из изгибающих моментов М_Х или М_Y. Поэтому все методические приемы оценки прочности остаются такими же, как и для случая косого изгиба с растяжением-сжатием.

2. Условие прочности для прямого изгиба с растяжением-сжатием имеет вид в зависимости от особенностей нагружения и формы сечения:

• При наличии внутреннего изгибающего момента М_Х и продольной силы N:

; (3.2)

• При наличии внутреннего изгибающего момента М_Y и продольной силы N:

; (3.3)

• При наличии моментов М_X и М_Y, но для форм сечений, исключающих косой изгиб (круг и правильные многоугольники):

, (3.4)

где , W_ос – осевой момент сопротивления поперечного сечения относительно оси изгиба (нейтральной линии).

Алгоритм расчета на прочность при косом (прямом) изгибе с растяжением-сжатием

1. Определение положение опасного сечения на элементе конструкции по эпюрам (эпюре) изгибающих моментов.

2. Определение положения опасной точки в опасном сечении.

1. При наличии двух прямых изгибов нужно построить силовую линию в плоскости опасного сечения. Как построить силовую линию подробно смотри в теме 2 во втором пункте алгоритма (стр. 30). В случае прямоугольного сечения, двутавра или швеллера опасными от изгибающих моментов будут угловые точки в силовых четвертях. Для круглого сечения опасные точки будут на пересечении силовой линии с контуром сечения. Одна из опасных точек от изгиба будет испытывать растягивающее нормальное напряжение со знаком «+», а противоположная точка – сжимающее нормальное напряжение со знаком «–». В каждую из опасных точек от изгиба надо приписать знак нормального напряжения от продольной силы N в случае растяжения «+» или «–» в случае сжатия. Точка, в которой знаки нормальных напряжений совпадут, будет опасной точкой сечения.

2. При наличии одного внутреннего изгибающего момента силовой линией является та ось поперечного сечения, с которой совпадает ордината изгибающего момента. Ось, перпендикулярная силовой является нейтральной. Точки, максимально отстоящие от нейтральной линии, являются опасными от изгиба. Те точки, которые находятся в зоне сжатия испытывают нормальное напряжение со знаком «–», а противоположные в зоне растяжения – со знаком «+». Осталось только добавить знаки нормальных напряжений от действия продольной силы. Опасными будут, соответственно, те точки, в которых совпадут знаки напряжений.

3. Запись одного из условий прочности (3.1)÷(3.4) и его решение в соответствии поставленной задачи. При реализации этого пункта алгоритма чаще всего напряжением от действия нормальной силы пренебрегают. Во-первых, потому, что оно гораздо меньше по сравнению с напряжением, возникающим от изгибающего момента и, во-вторых, включает величину характерного размера в квадрате, а напряжение от изгибающего момента – в кубе, что затрудняет, например, решение задачи об определении величины характерного размера поперечного сечения. После определения величины характерного размера по составляющей напряжения от изгиба проводят проверку прочности с учетом напряжения от действия продольной силы. Если процент перенапряжения не превышает пяти, принимают найденные величины в качестве действительных. В противном случае, их изменяют методом подбора.