Задача 2

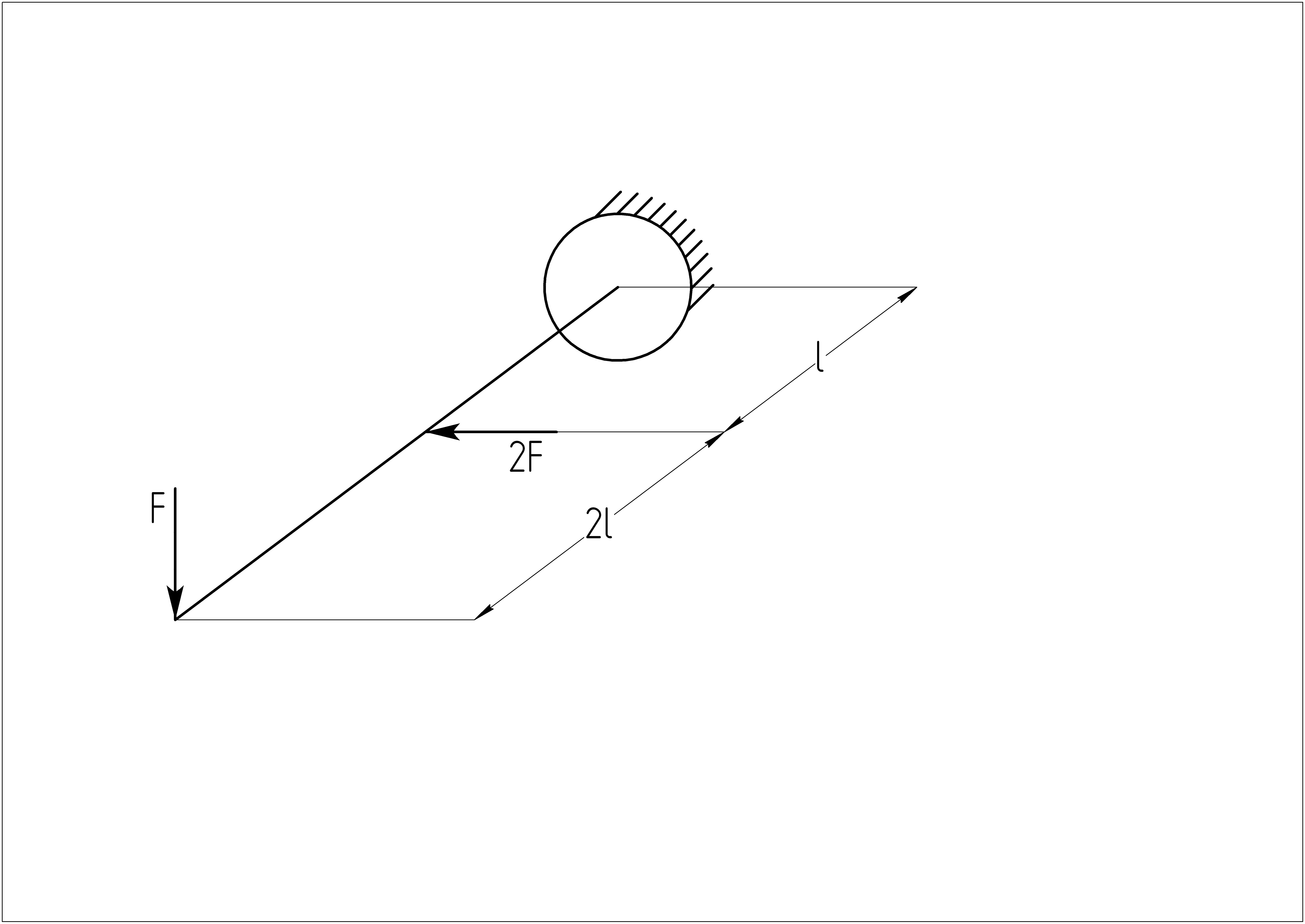
Стержень консольного типа нагружен двумя силами величиной F в вертикальной плоскости и величиной 2F в горизонтальной плоскости. Параметр длины . Изготовлен стержень из Ст3 с допускаемым напряжением [σ]=160 МПа.

Требуется:

1. Определить грузоподъемность стержня [F] из условия прочности по допускаемому напряжению для прямоугольного сечения с соотношением сторон и величиной ;

2. Определить грузоподъемность стержня [F] из условия прочности по допускаемому напряжению для круглого сечения, равного по площади прямоугольному профилю.

Решение

1. Определим положение опасного сечения, для чего построим эпюры изгибающих моментов М_Y и М_Х на одной базе:

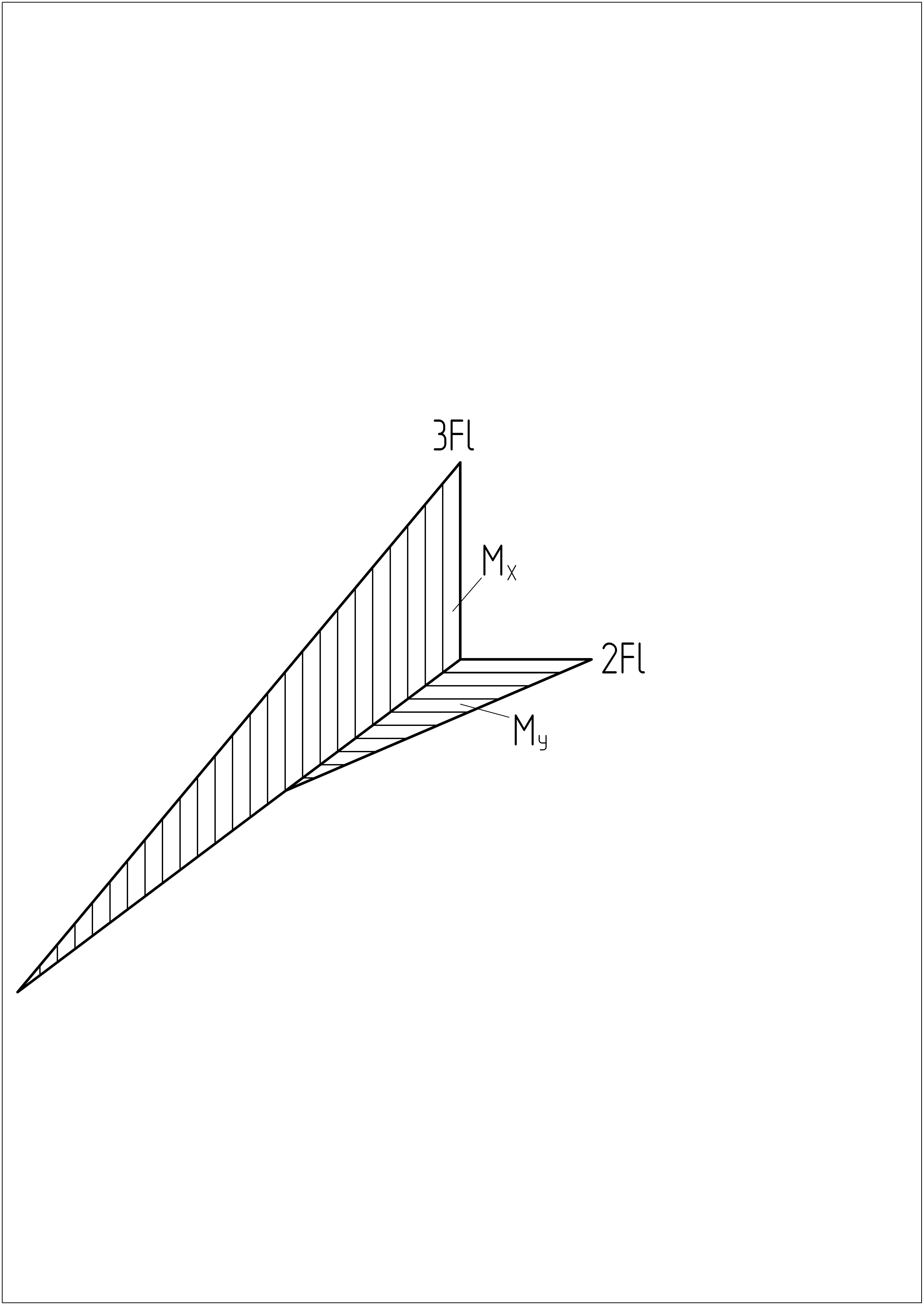
Из эпюр видно, что опасное сечение находится в заделке с моментами М_Х=3Fl и М_Y=2Fl.

2. Определим положение силовой линии в плоскости прямоугольного и круглого сечений. Для этого с сохранением масштаба перенесем ординаты изгибающих моментов с эпюр М_X и М_Y в опасном сечении в плоскость прямоугольного и круглого сечений и определим величину и направление ординаты суммарного момента , как геометрическую сумму моментов М_X и М_Y.

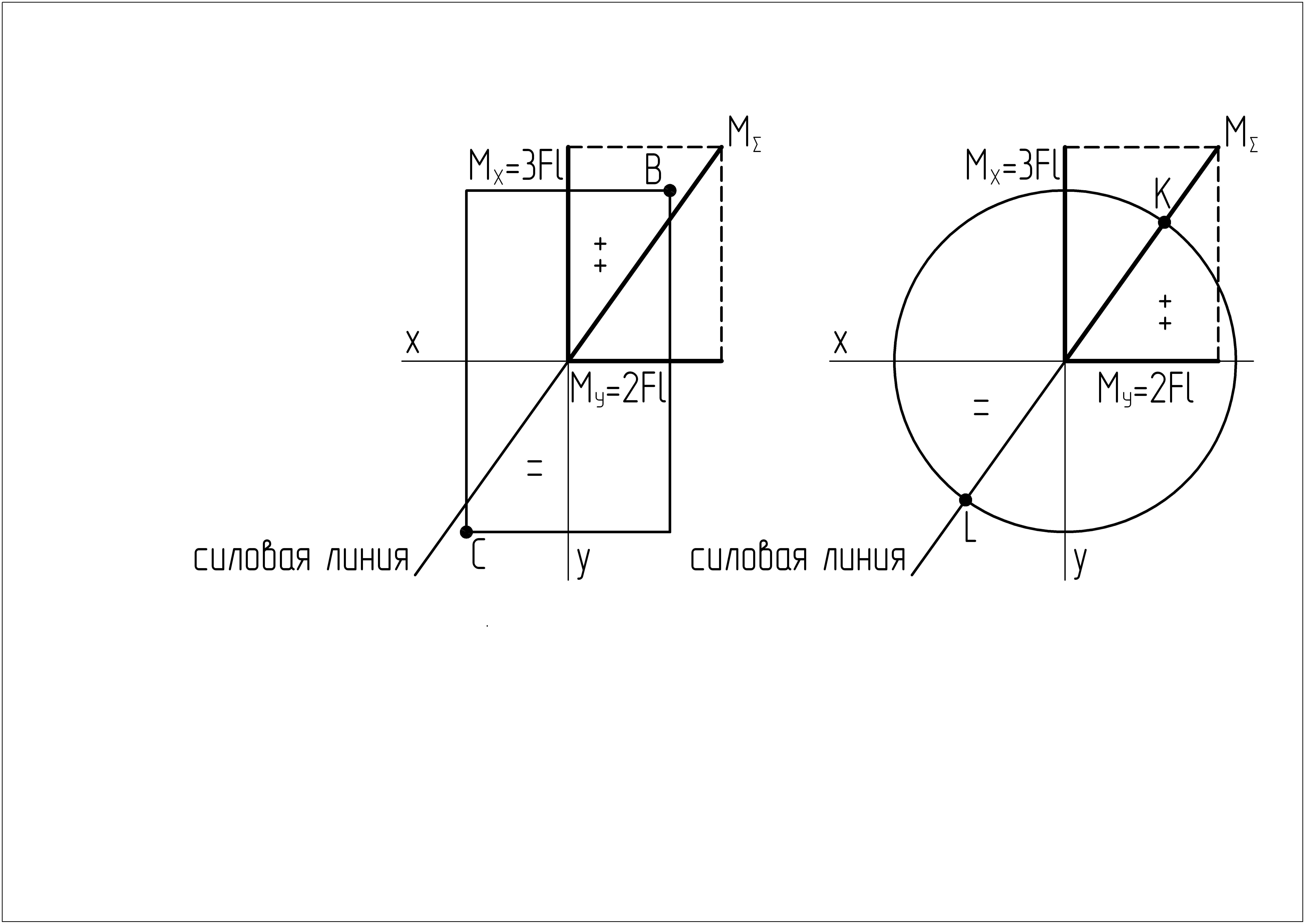
3. Определим положение опасных точек в опасном сечении. В прямоугольном сечении опасными будут угловые точки «В» и «С» в силовых четвертях, а в круглом сечении точки «К» и «L» на концах диаметра, совпадающего с силовой линией.

4. Запишем условие прочности для опасных точек прямоугольного профиля и определим из его решения величину грузоподъемности [F]:

.

Предварительно выразим моменты сопротивления через характерный размер b поперечного сечения:

; .

После подстановки численного значения изгибающих моментов в сечении заделки и выражений для моментов сопротивления через размер b получим:

, откуда .

5. Для круглого сечения определим из условия равенства площадей прямоугольного и круглого сечений величину диаметра:

.

6. Для опасных точек круглого сечения «К» и «L» запишем условие прочности:

, где .

Подставив в условие прочности, получим:

, откуда

.

Задача решена.

3. Потренируемся?

• Пройти тестовый тренинг (Приложение 1, тесты к теме 2, стр. 98)

Тема 3. Расчет на прочность при совместном действии изгиба и растяжения-сжатия

Цель занятия:

Научиться оценивать прочность конструкции, находящейся в условиях совместного действия изгиба и растяжения-сжатия. Понимать особенности этого вида деформации и учитывать их в расчетной практике.

Необходимые знания для достижения цели:

1. Что такое косой изгиб с растяжением-сжатием.

2. Формулы для определения нормальных напряжений от изгибающих моментов и внутренней продольной силы.

3. Принцип алгебраического сложения однотипных напряжений, возникающих от разных внутренних силовых факторов.

1. Теоретический материал

3.1.1. Случай косого изгиба с растяжением-сжатием

Что такое косой изгиб с растяжением-сжатием?

Совокупность косого изгиба, при котором силовая линия не совпадает ни с одной из главных центральных осей сечения, с одновременным силовым воздействием в направлении продольной оси элемента конструкции приводит к данному случаю деформации. Например:

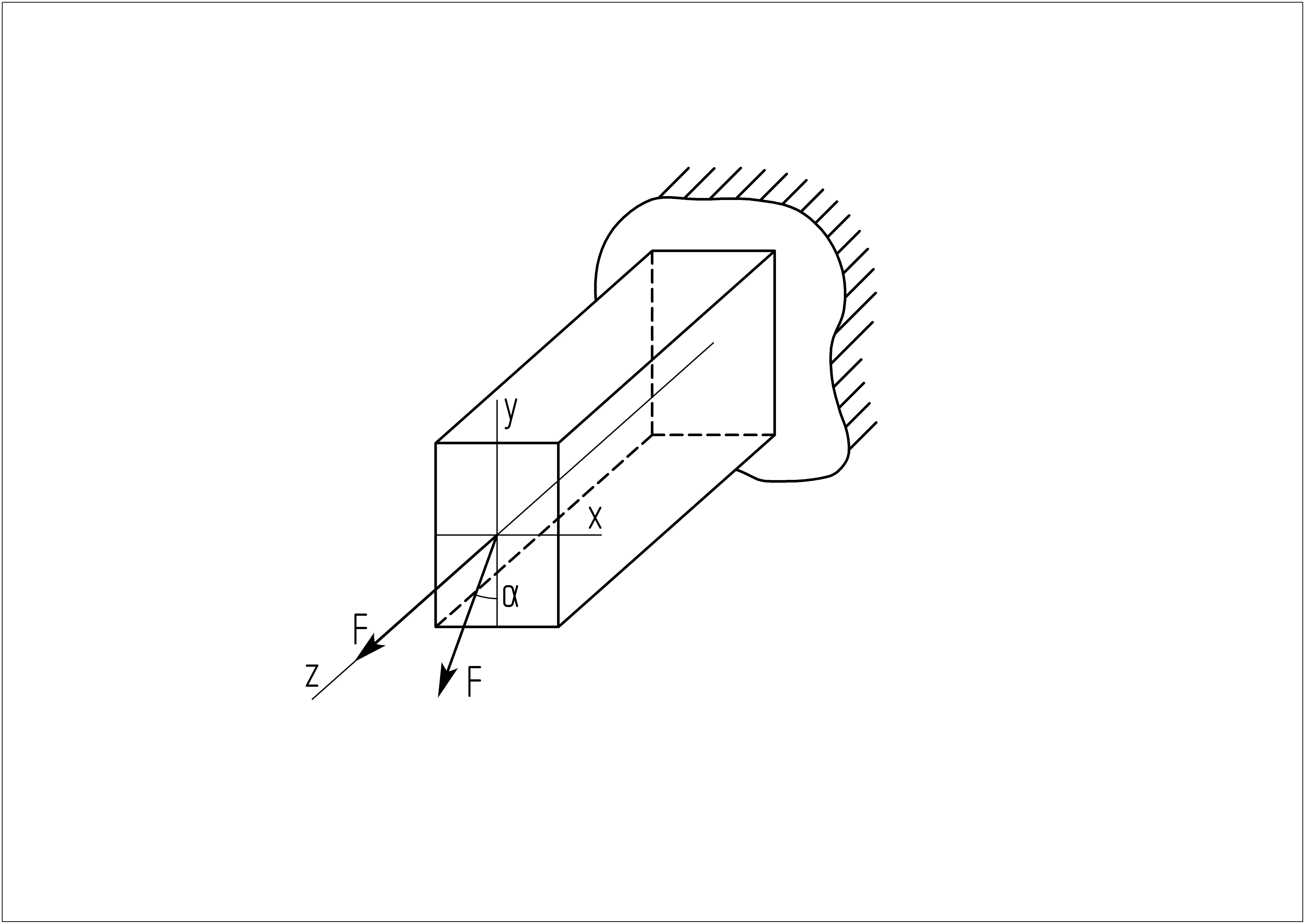
Чтобы научиться оценивать прочность

в случае косого изгиба с растяжением-сжатием надо знать!

1. Что оценка напряжений в опасной точке элемента конструкции ведется отдельно от каждого внутреннего силового фактора, возникающего при данном виде деформации.

2. Поскольку присутствует косой изгиб, то в первую очередь определяют положение опасных точек от косого изгиба.

3. В зависимости от того, что добавляется к косому изгибу (деформация растяжения или сжатия), в опасные точки от действия изгибающих моментов будет добавляться, соответственно, положительное или отрицательное напряжение от продольной силы.

4. Условие прочности при косом изгибе с растяжением-сжатием имеет следующий вид:

. (3.1)

5. Если материал элемента конструкции пластичный, т.е. имеет одинаковые пределы текучести при растяжении и сжатии, то расчет напряжений в опасной точке сжатой зоны ведется по модулю.