2. Примеры решения задач Задача 1

Консольный стержень прямоугольного сечения на свободном конце нагружен сосредоточенной силой F=10кН, вектор которой проходит через центр тяжести сечения под углом 30˚ к вертикальной оси y. Длина стержня , а соотношение сторон прямоугольного сечения . Стержень изготовлен из Ст 3 с допускаемым напряжением [σ]=160МПа.

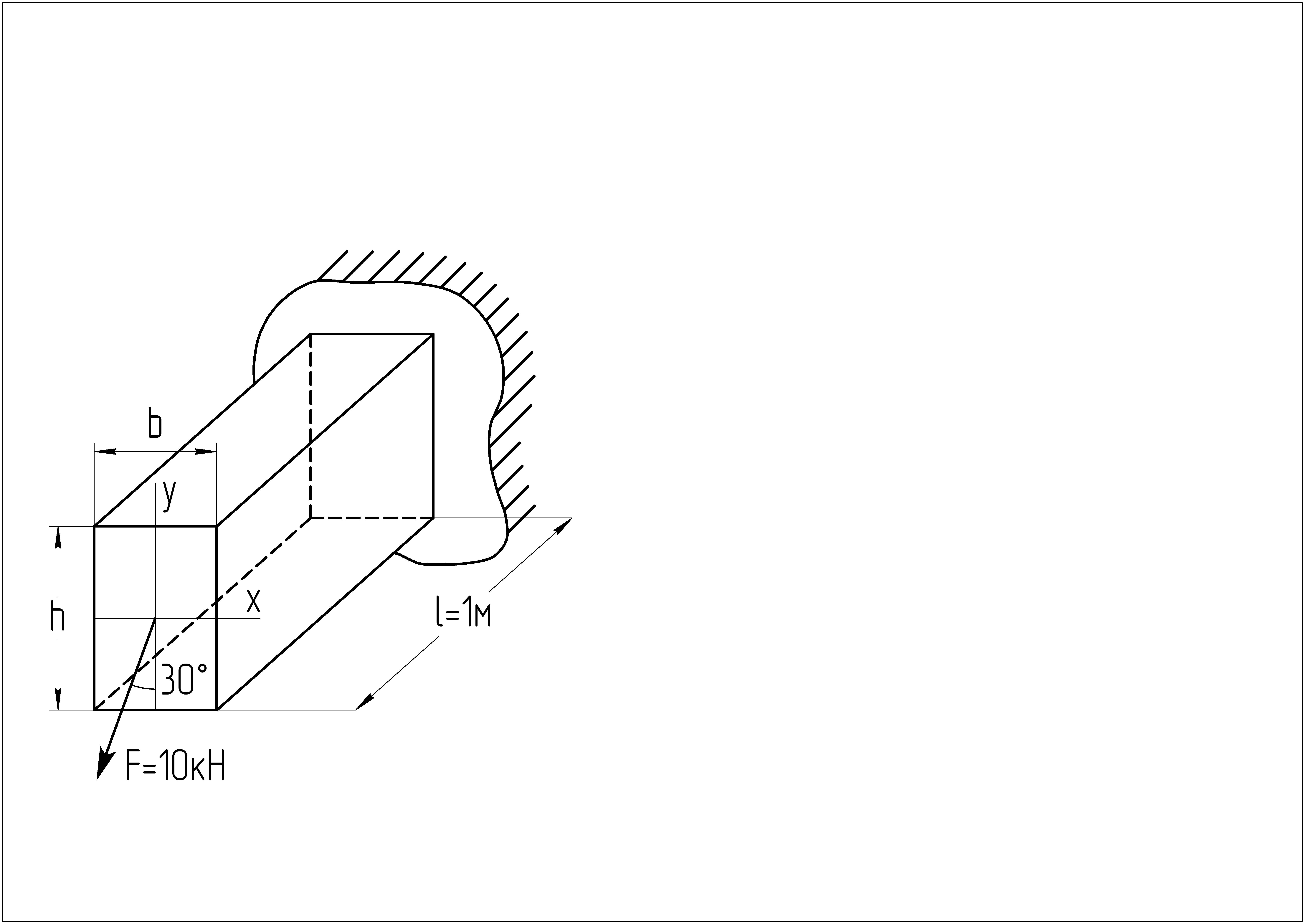
Требуется:

1. Определить из условия прочности по допускаемым напряжениям величину характерного размера прямоугольного сечения [b].

2. Заменив прямоугольное сечение стержня круглым, определить величину диаметра круглого сечения [d] из условия прочности.

3. Сравнить металлозатраты стержней прямоугольного и круглого поперечных сечений.

Решение

1. Определим положение опасного сечения. Для этого спроектируем силу F на главные центральные оси Х и Y поперечного сечения: 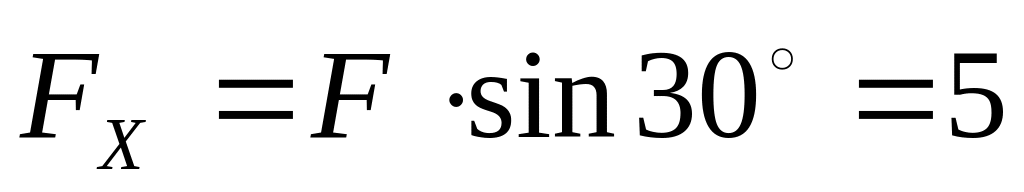кН; 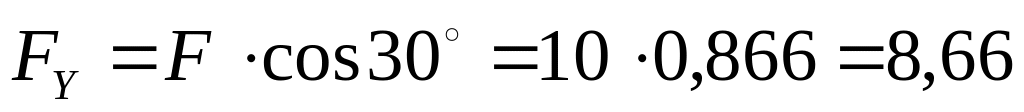кН. Затем от каждой из этих сил построим эпюры изгибающих моментов на одной базе М_Y и М_Х, соответственно. Опасное сечение будет в заделке, т.е. в том сечении, где моменты достигают своего максимального значения.

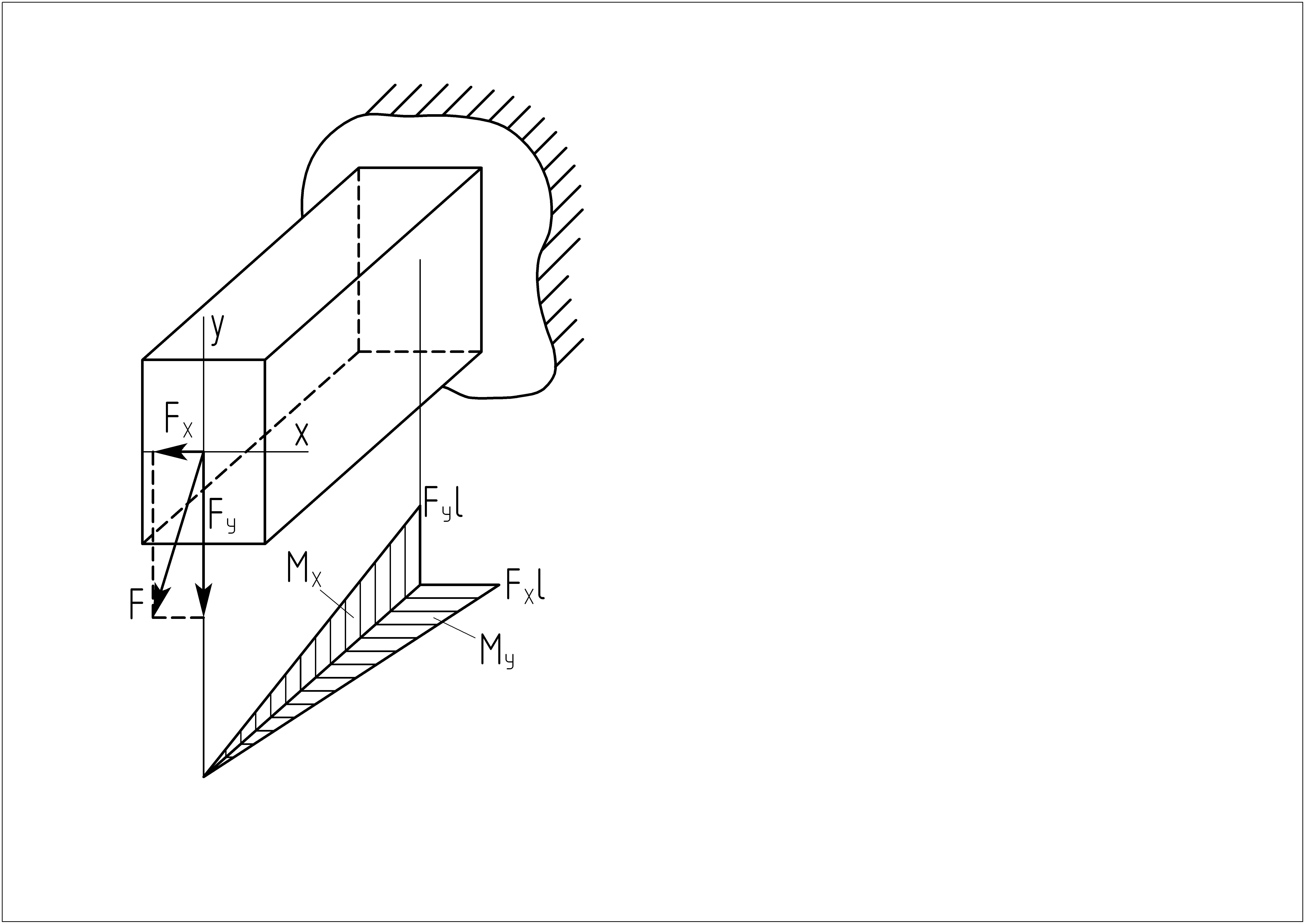
2. Определим положение силовой линии в опасном сечении. Для этого изобразим сечение, в плоскости которого отложим в масштабе значения изгибающих моментов М_Y и М_X в ту же сторону, что на эпюрах соответствующих моментов: М_Y отложим вправо, а М_X отложим вверх. Т.к. эпюры построены на растянутых волокнах, то растянуты правые волокна стержня относительно оси «у» от действия момента М_Y и, соответственно, там поставим знаки «+» в I и IV четвертях сечения, а в противоположных II и III знаки «–» (нумерацию четвертей прямоугольника смотри ниже). Также растянуты верхние волокна стержня относительно оси «х» от момента М_X и, соответственно, поставим знаки «–» нормального напряжения в I и II четвертях, а в нижних (Ш и IV) четвертях знаки «+». Тогда ордината суммарного момента пройдет через I и III четверти и определит положение силовой линии. В этих же четвертях совпадают знаки нормальных напряжений от изгибающих моментов М_X и М_Y:

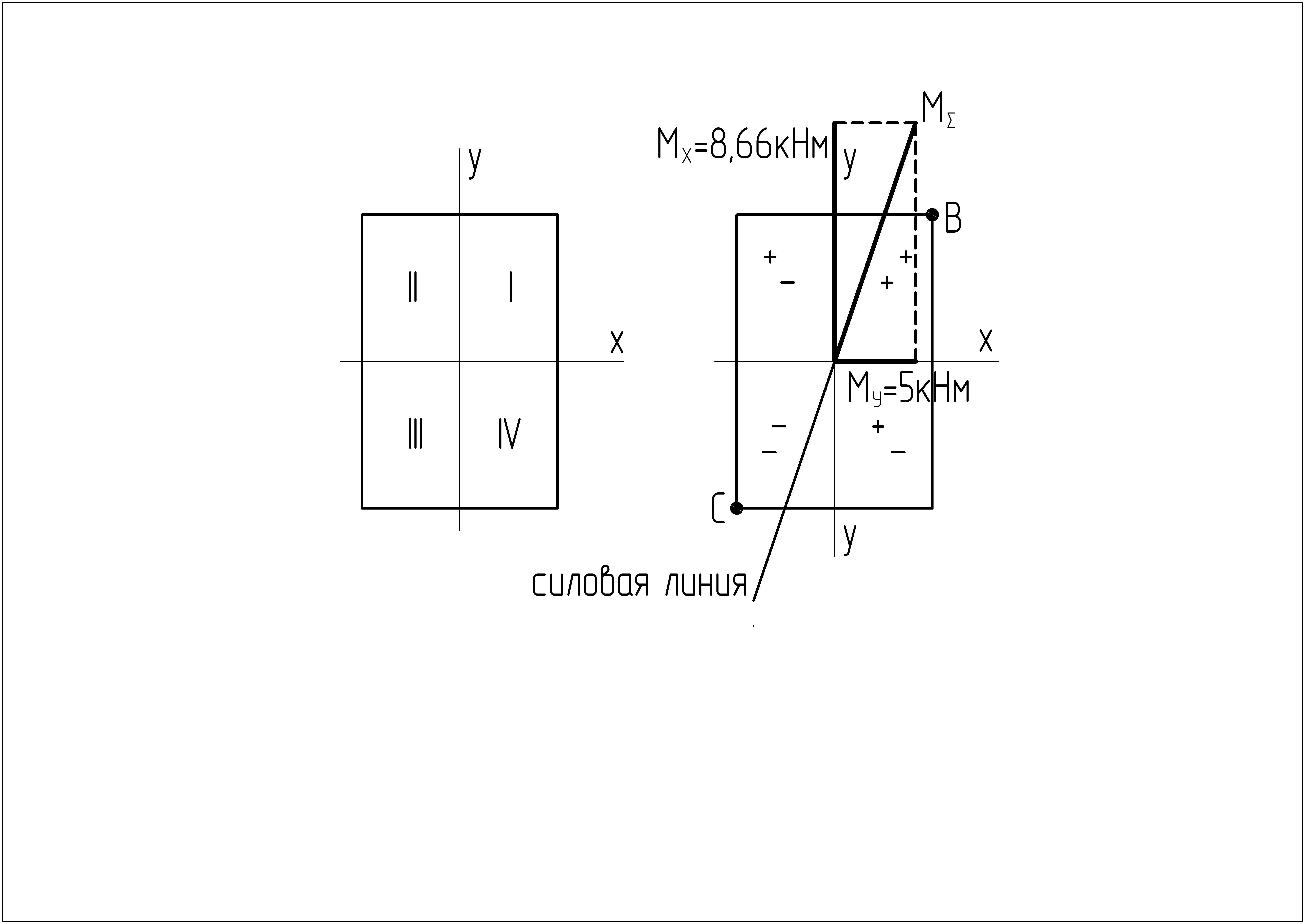
3. Определим положение опасных точек в опасном сечении. Это будут угловые точки в силовых четвертях, т.е. точки «В» и «С». Точки являются равноопасными точками, т.к. величины напряжений в них будут одинаковыми по абсолютной величине. В точке «С» – угловой точке третьей четверти с двумя знаками «–» нормальных напряжений от двух прямых изгибов возникает максимальное сжимающее напряжение. Противоположная ей точка «В» попала в область растяжения (два знака «+» от прямых изгибов) и напряжение в ней будет положительным: .

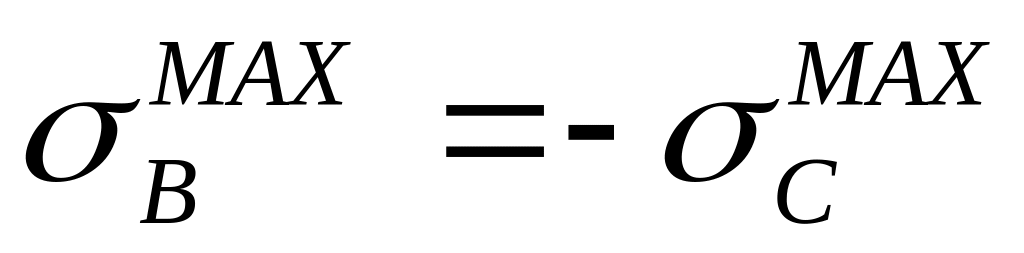4. Запишем условие прочности для опасных точек и определим из его решения величину размера поперечного сечения:

.

Предварительно выразим моменты сопротивления поперечного сечения через характерный размер b.

; .

После подстановки численного значения изгибающих моментов в сечении заделки и выражений для моментов сопротивления через размер b получим:

, откуда .

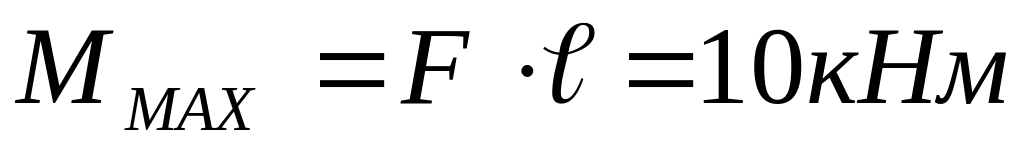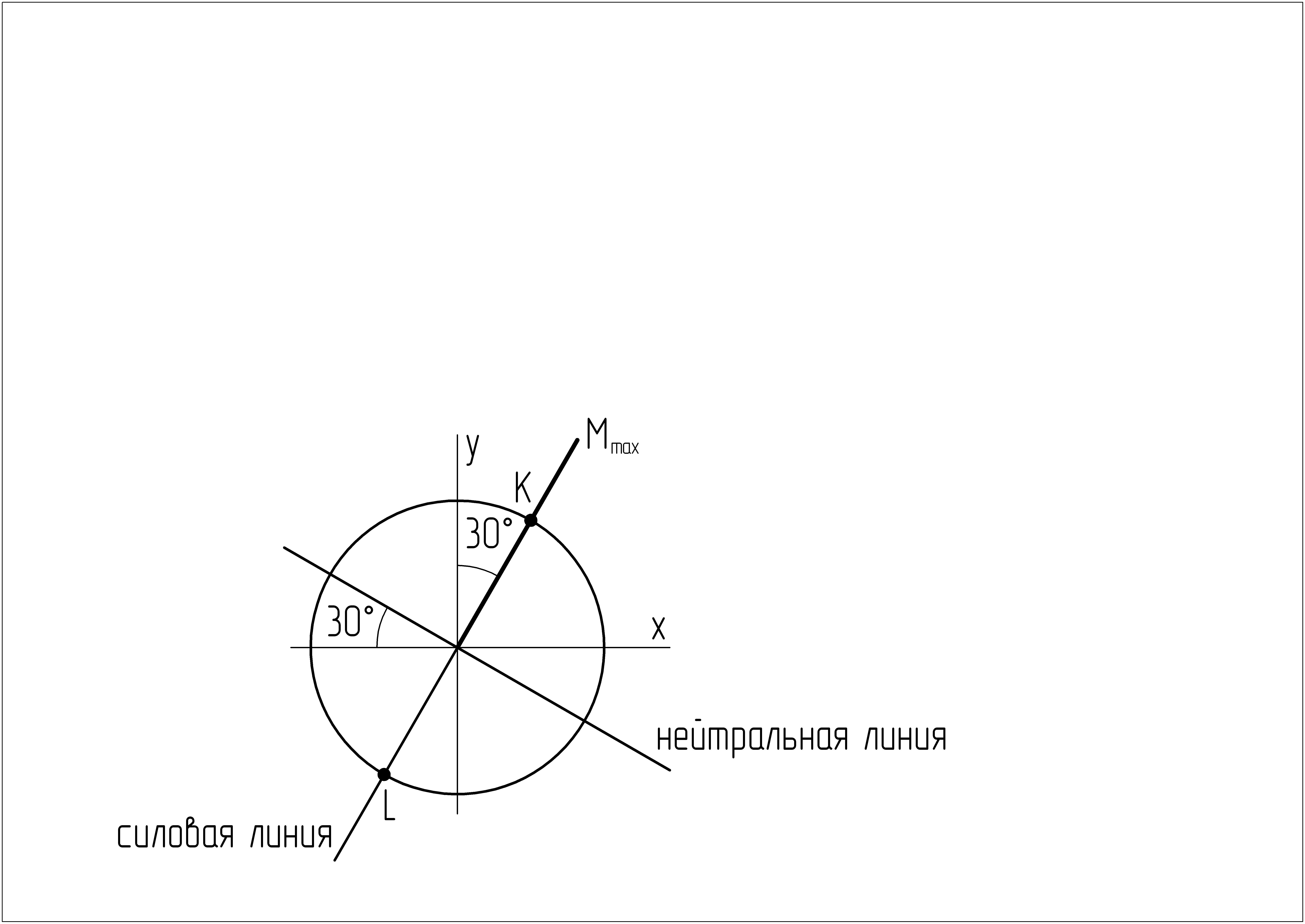
5. Для определения диаметра круглого сечения для данного стержня определим внутренний изгибающий момент в заделке: . В плоскости опасного сечения проведем ординату максимального момента под углом в 30˚ к оси y и продлим ее до пересечения с контуром сечения. Это и будет силовой линией. Нейтральная линия проходит перпендикулярно силовой линии. Опасными точками будут точки, расположенные на максимальном расстоянии от нейтральной линии. Это точки «К» и «L», находящиеся на концах диаметра, совпадающего с силовой линией. Направление вектора внешней силы F указывает на сжатую зону. Т.е. половина сечения выше нейтральной линии растянута и точка «К» испытывает положительные напряжения. Соответственно, точка «L» – отрицательные напряжения.

6. Запишем условие прочности по формуле прямого изгиба:

.

Для круглого сечения момент сопротивления через диаметр определяется как:

Подставив в условие прочности значение момента и выражение для W_X , получим:

, откуда .

7. Сравним стержни прямоугольного и круглого сечений по металлозатратам. Для этого определим площади сечений:

,

т.е. для случая косого изгиба (прямоугольный профиль) требуется большее по площади сечение, что указывает на более опасный характер этого вида деформации для данных исходных условий.

Задача решена.