Алгоритм расчета на прочность при косом изгибе

1. Определение положение опасного сечения на элементе конструкции по эпюрам внутренних моментов 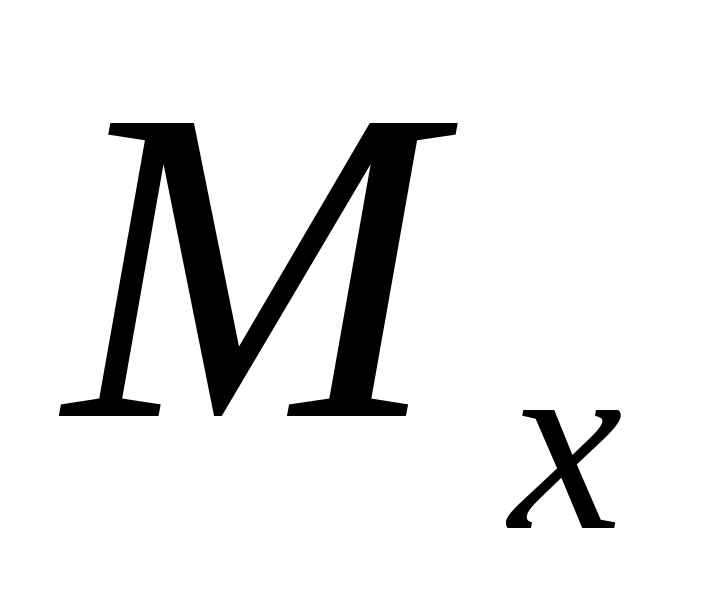и М_у, построенных от действия внешних нагрузок.

2. Определение положения силовой линии в опасном сечении. Для этого необходимо в плоскости сечения по осям х и у отложить в масштабе ординаты внутренних моментов (М_х по оси у, а М_у по оси х) в сторону, соответствующую положению ординат на эпюрах изгибающих моментов в опасном сечении. Ордината суммарного момента, построенная как геометрическая сумма ординат моментов М_х и М_y, определяет положение силовой линии.

3. Определение положения опасных точек в опасном сечении. Для сечения прямоугольной формы и подобной ему (двутавр, швеллер), опасные точки – это угловые точки в силовых четвертях. Они равноопасны, т.к. находятся на одинаковых расстояниях от главных центральных осей сечения.

4. Запись условия прочности для опасных точек и его решение согласно поставленной задаче:

.

Для прямоугольного сечения можно воспользоваться «зеркальной» формулой для определения нормальных напряжений от каждого изгибающего момента, создающего прямой изгиб:

,

где и – моменты сопротивления поперечного сечения относительно соответствующих главных центральных осей.

2.1.2. Случаи исключения

Имеются формы поперечных сечений, для которых косой изгиб невозможен. Это сечения, у которых любая пара центральных осей является главной. И, как бы ни проходила силовая линия, она всегда совпадет с главной центральной осью. Это такие профили, как круг и все правильные многоугольники, например, равносторонний треугольник, квадрат и т.д. Для этих форм профилей изгиб всегда прямой. Нейтральная линия, соответственно, перпендикулярна силовой линии.

Как же быть в таком случае?

• Если элемент конструкции нагружен одной нагрузкой, под углом к осям заданной системы координат, то расчет напряжений ведется по формуле прямого изгиба от максимального момента, созданного этой нагрузкой. Линия действия нагрузки является силовой линией, а нейтральная линия проходит перпендикулярно силовой. Опасные точки находятся на максимальном расстоянии от нейтральной линии, напряжения в которых определяются по формуле: . Для круглого профиля эти точки находятся на пересечении силовой линии с контуром сечения и напряжения в них можно определить по зеркальной формуле , где , d – диаметр круглого профиля.

• Если элемент конструкции нагружен силами, вектора которых лежат в двух взаимно перпендикулярных плоскостях, то в опасном сечении по осям сечения х и у откладываются величины ординат внутренних изгибающих моментов (М_х по оси у, а М_у по оси х) в сторону, соответствующую положению ординат на эпюрах изгибающих моментов в соответствующем сечении. Находится величина и положение ординаты суммарного внутреннего момента , который и определяет положение силовой линии. Далее нахождение опасных точек и напряжений в них производится аналогично предыдущему случаю.