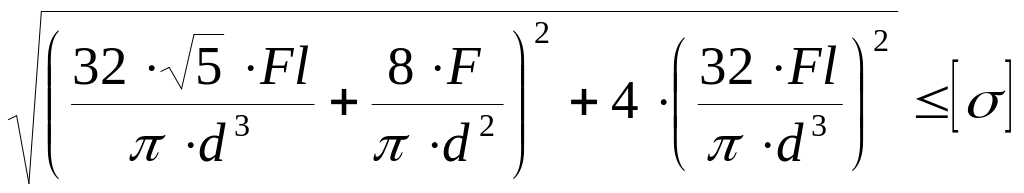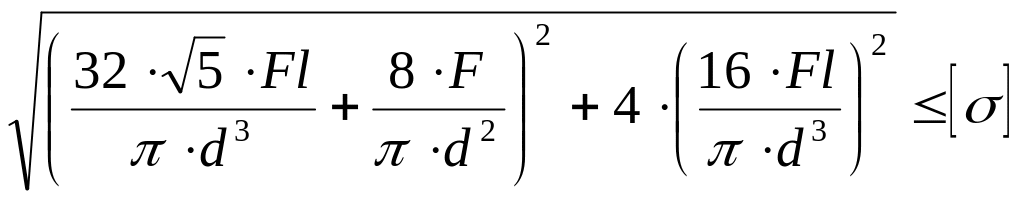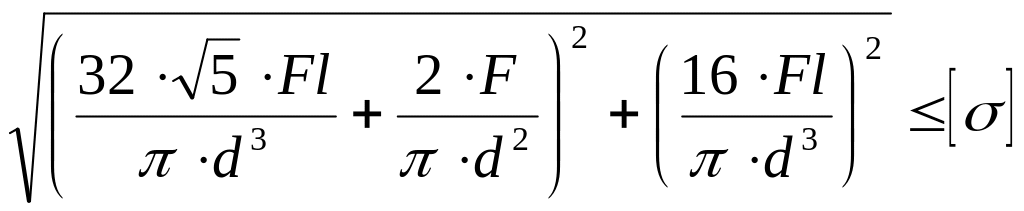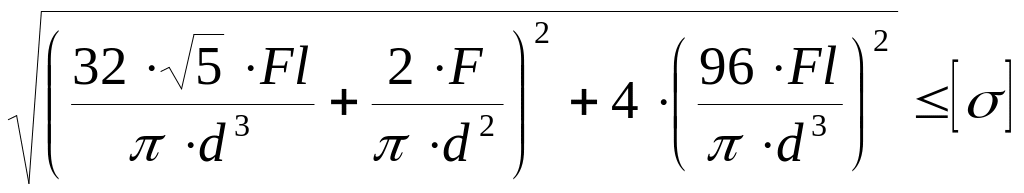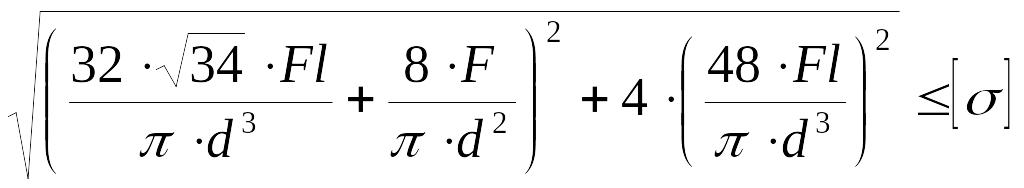- •Сопротивление материалов практикум
- •Часть 2
- •Тема 1. Расчет статически неопределимых систем методом сил
- •Теоретический материал
- •Алгоритм метода сил
- •1. Определение степени статической неопределимости.
- •2. Выбор основной системы.
- •3. Образование эквивалентной системы.
- •4. Запись условия эквивалентности.
- •5. Определение коэффициентов системы канонических уравнений метода сил.
- •5.1. Построение вспомогательных эпюр всф.
- •Пример решения задачи
- •Потренируемся?
- •Тема 2. Расчет на прочность при косом изгибе. Случаи исключения
- •Теоретический материал
- •2.1.1. Случай косого изгиба
- •Алгоритм расчета на прочность при косом изгибе
- •2.1.2. Случаи исключения
- •Примеры решения задач Задача 1
- •Задача 2
- •Тема 3. Расчет на прочность при совместном действии изгиба и растяжения-сжатия
- •Теоретический материал
- •3.1.1. Случай косого изгиба с растяжением-сжатием
- •3.1.2. Случай прямого изгиба с растяжением-сжатием
- •Алгоритм расчета на прочность при косом (прямом) изгибе с растяжением-сжатием
- •Пример решения задачи Задача
- •Потренируемся?
- •Тема 4. Расчет на прочность при изгибе с растяжением-сжатием и кручением
- •Теоретический материал
- •Круглое поперечное сечение
- •Прямоугольное поперечное сечение
- •Алгоритм расчета на прочность при изгибе с кручением и растяжением-сжатием
- •4.2 Пример решения задачи
- •2.1. Расчет на прочность для элемента II (bc)
- •2.2. Проверка на прочность для элемента I (ab)
- •3.1. Расчет на прочность для элемента II (bc)
- •3.2. Проверка на прочность для элемента I (ab)
- •4.3. Потренируемся?
- •Тема 5. Расчет сжатых стоек на устойчивость
- •Теоретический материал
- •Пример решения задачи Задача 1
- •Задача №2
- •Потренируемся?
- •Тема 6. Расчет на усталостную прочность
- •Теоретический материал
- •Алгоритм построения схематизированной диаграммы предельных амплитуд и графический метод определения коэффициента запаса усталостной прочности
- •Пример расчета
- •Потренируемся?
- •Тема 7. Расчет на прочность подмоторных элементов с одной степенью свободы в условиях вынужденных колебаний
- •Теоретический материал
- •Алгоритм расчета на прочность при вынужденных колебаниях упругих систем с одной степенью свободы
- •Пример решения задачи
- •Потренируемся?
- •Тема 8. Расчет на прочность и жесткость упругих элементов от действия ударной нагрузки
- •8.1. Теоретический материал
- •Алгоритм расчета на прочность и жесткость при поперечном ударе
- •8.2. Пример решения задачи
- •8.3. Потренируемся?
- •Вариант 2
- •Тесты к теме 2 «Косой изгиб» Вариант 1
- •Вариант 2
- •Тесты к теме 3 «Изгиб с растяжением-сжатием» Вариант 1
- •Вариант 2
- •Тесты к теме 4 «Расчет на прочность при изгибе с растяжением-сжатием и кручением» Вариант 1
- •Вариант 2
- •Тесты к теме 5 «Расчет сжатых стоек на устойчивость» Вариант 1
- •Вариант 2
- •Тесты к теме 6 «Расчет на усталостную прочность» Вариант 1
- •Вариант 2
- •Тесты к теме 7 «Расчет на прочность подмоторных элементов с одной степенью свободы в условиях вынужденных колебаний» Вариант 1
- •Вариант 2
- •Тесты к теме 8 «Расчет на прочность и жесткость упругих элементов от действия ударной нагрузки» Вариант 1
- •Вариант 2
- •Приложение 2. Ответы к тестам
- •Приложение 3. Задания для выполнения контрольных работ Правила оформления и выполнения контрольных работ
- •Контрольная работа №1
- •Задача 1.1. Расчет на прочность и жесткость статически неопределимых балок
- •План решения
- •Задача 1.2. Расчет на прочность при сложном сопротивлении
- •План решения
- •План решения
- •Задача 2.2. Расчет на прочность при повторно-переменных нагрузках
- •План решения
- •План решения
- •Приложение 4. Справочный материал Приложение 4.1. Сортамент прокатной стали Двутавры стальные горячекатаные
- •Швеллеры стальные горячекатаные
- •Уголки стальные горячекатаные равнополочные
- •Уголки стальные горячекатаные неравнополочные
- •Приложение 4.2. Данные по расчету на кручение стержней прямоугольного сечения
- •Приложение 4.3. Данные к расчетам на устойчивость Коэффициенты продольного изгиба
- •Значения коэффициентов, входящих в эмпирическую формулу Ясинского для критической силы, и пределы применимости этой формулы
- •Приложение 4.4. Данные к расчету характеристик сопротивления усталости Значения эффективных коэффициентов концентрации
- •Значения эффективных коэффициентов концентрации нормальных напряжений для валов с выточками
- •Значения эффективных коэффициентов концентрации напряжений и для валов с поперечными отверстиями
- •Значения эффективных коэффициентов концентрации напряжений и для валов с одной шпоночной канавкой
- •Значения масштабных факторов и
- •Значения коэффициентов влияния состояния обработанной поверхности
- •Содержание
- •Тема 1. Расчет статически неопределимых систем методом сил. . . . . . . . . . . 3
- •Сопротивление материалов практикум
- •Часть 2
- •445667, Г.Тольятти, ул.Белорусская, 14
Тесты к теме 4 «Расчет на прочность при изгибе с растяжением-сжатием и кручением» Вариант 1
Консольная рама, состоящая из двух элементов одинаковой длины l, изготовлена из пластичного материала и нагружена пространственной системой внешних сил.
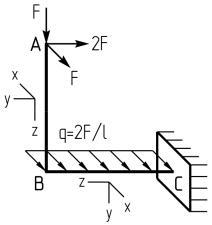
Эпюры внутренних силовых факторов построены:
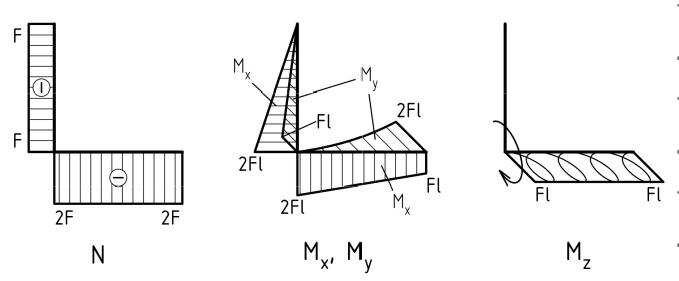
Поперечное сечение рамы круглое с диаметром d или прямоугольное с соотношением длин сторон h/b = 2 и значениями коэффициентов β = 0,493, γ = 0,795.
Используйте, при необходимости, III теорию предельного состояния.
Какое сечение данной рамы является наиболее опасным в случае круглой формы поперечного сечения?
Сечение «B» элемента AB
Сечение «B» элемента BC
Сечение «C»
Сечение «B» элемента BC и «C» равноопасны
Как располагается силовая линия в плоскости круглого поперечного сечения «C» данной рамы?
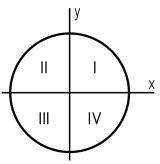
Совпадает с осью y
Проходит через четверти I и III
Совпадает с осью x
Проходит через четверти II и IV
Какая точка круглого поперечного сечения «C» данной рамы является опасной?
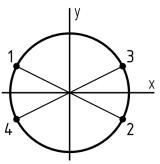
Точка «1»
Точка «2»
Точка «3»
Точка «4»
Как записывается условие прочности для опасной точки круглого поперечного сечения «C» данной рамы?
Какая форма рамы является более рациональной в случае прямоугольного поперечного сечения?
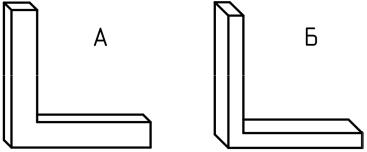
«А»
«Б»
Оба варианта равнозначны
Как располагается силовая линия в плоскости прямоугольного поперечного сечения «C» данной рамы?
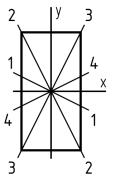
1-1
2-2
3-3
4-4
Какая тройка точек лежит в опасной четверти прямоугольного поперечного сечения «C» данной рамы?
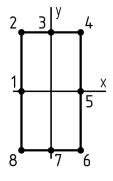
Точки «1», «2», «3»
Точки «3», «4», «5»
Точки «5», «6», «7»
Точки «7», «8», «1»
Как записывается условие прочности для точки, находящейся в вершине опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
Как записывается условие прочности для точки, находящейся посередине длинной стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
Как записывается условие прочности для точки, находящейся посередине короткой стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
Вариант 2
Консольная рама, состоящая из двух элементов одинаковой длины l, изготовлена из пластичного материала и нагружена пространственной системой внешних сил.
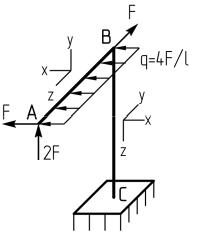
Эпюры внутренних силовых факторов построены:
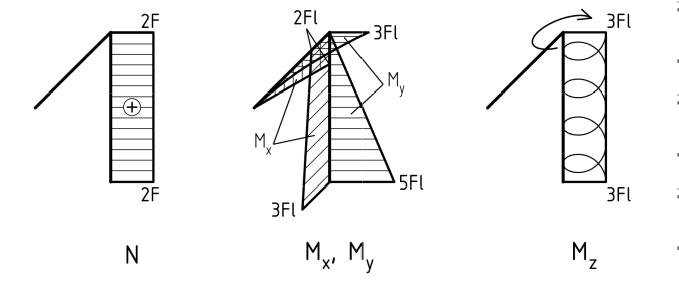
Поперечное сечение рамы круглое с диаметром d или прямоугольное с соотношением длин сторон h/b = 2 и значениями коэффициентов β = 0,493, γ = 0,795.
Используйте, при необходимости, III теорию предельного состояния.
Какое сечение данной рамы является наиболее опасным в случае круглой формы поперечного сечения?
Сечение «A»
Сечение «B» элемента AB
Сечение «B» элемента BC
Сечение «C»
Как располагается силовая линия в плоскости круглого поперечного сечения «C» данной рамы?
Совпадает с осью y
Проходит через четверти I и III
Совпадает с осью x
Проходит через четверти II и IV
Какая точка круглого поперечного сечения «C» данной рамы является опасной?
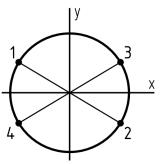
Точка «1»
Точка «2»
Точка «3»
Точка «4»
Как записывается условие прочности для опасной точки круглого поперечного сечения «C» данной рамы?
Какая форма рамы является более рациональной в случае прямоугольного поперечного сечения?
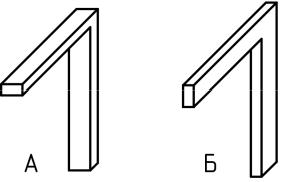
«А»
«Б»
Оба варианта равнозначны
Как располагается силовая линия в плоскости прямоугольного поперечного сечения «C» данной рамы?
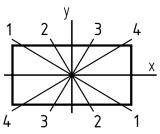
1-1
2-2
3-3
4-4
Какая тройка точек лежит в опасной четверти прямоугольного поперечного сечения «C» данной рамы?
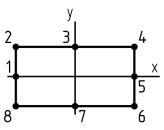
Точки «1», «2», «3»
Точки «3», «4», «5»
Точки «5», «6», «7»
Точки «7», «8», «1»
Как записывается условие прочности для точки, находящейся в вершине опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
в
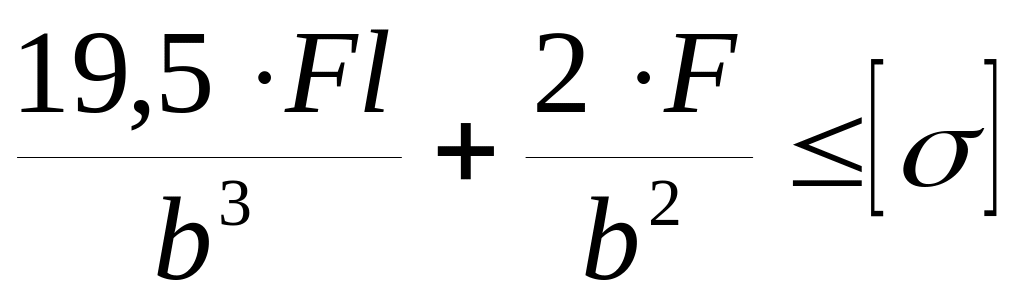
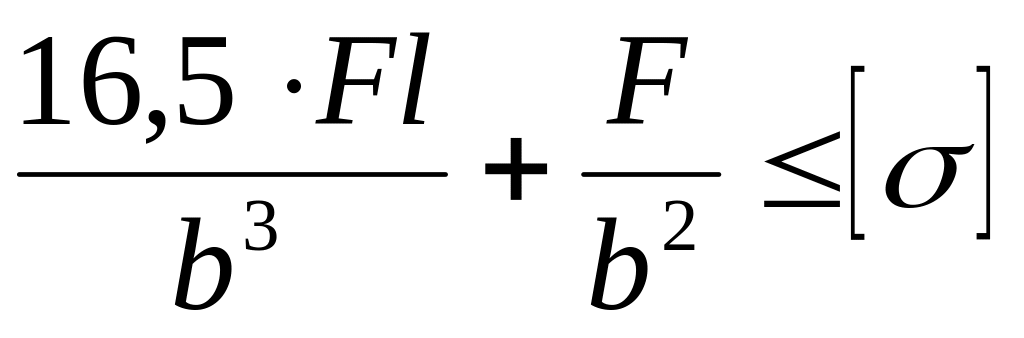
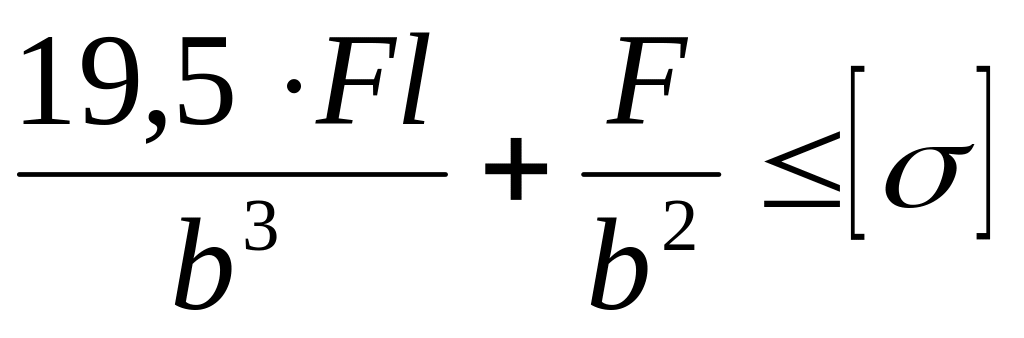
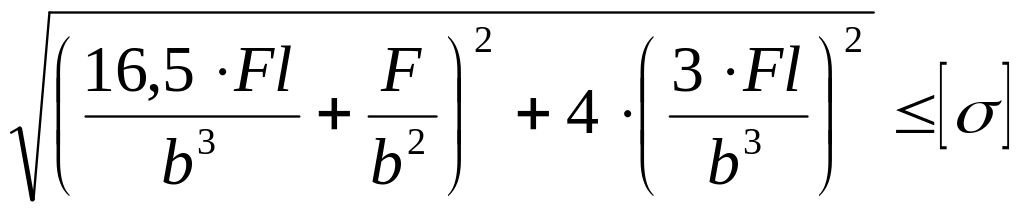
Как записывается условие прочности для точки, находящейся посередине длинной стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?
Как записывается условие прочности для точки, находящейся посередине короткой стороны в опасной четверти прямоугольного поперечного сечения «C» данной рамы, при указанном выше расположении сечения?