Алгоритм построения схематизированной диаграммы предельных амплитуд и графический метод определения коэффициента запаса усталостной прочности

1. Задать систему координат s_a – s_m.

2. На оси s_а  отложить в выбранном масштабе т. С – значение предела выносливости , известного по марке материала.

3. Из точки C, отложенной на оси sа  провести наклонную прямую СВ под углом α к горизонту, который нужно определить, как 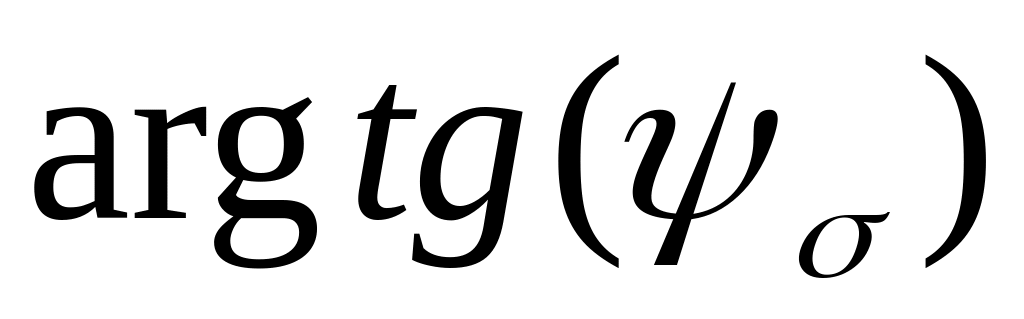, предварительно выписав из справочных таблиц значение .

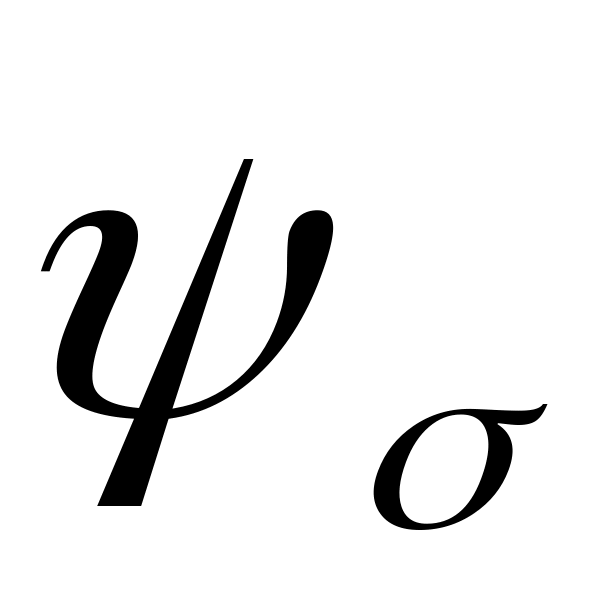4. На оси s_m отложить в выбранном масштабе т. D – значение предела текучести , также известного по марке материала.

5. Из точки D на оси s_m провести прямую DB под углом 45˚ до пересечения с прямой CB.

6. В полученной области диаграммы OCBD отложить точку S – рабочую точку с координатами рассчитанных режимов работы детали и 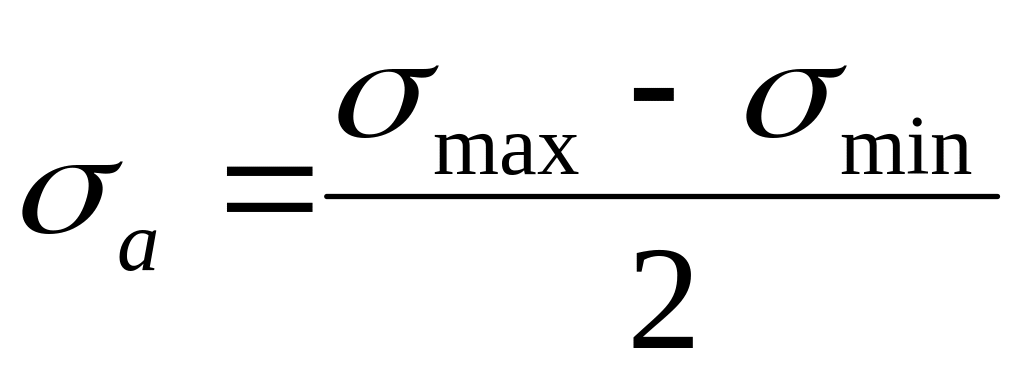, умножив последнее на поправочный коэффициент 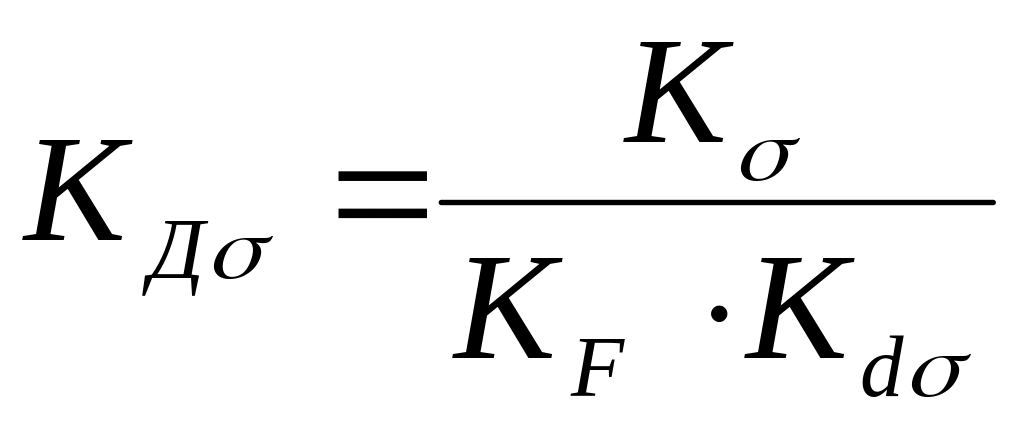, учитывающий особенности рассчитываемого элемента конструкции: наличие концентратора напряжений, качество обработки поверхности детали и масштабный фактор. Коэффициенты соответствующие перечисленным факторам берутся из справочных таблиц.

7. Провести отрезок через точки O и S до пересечения с предельной огибающей CBD (точка Р).

8. Замерить отрезки OP и OS. Вычислить коэффициент запаса усталостной прочности .

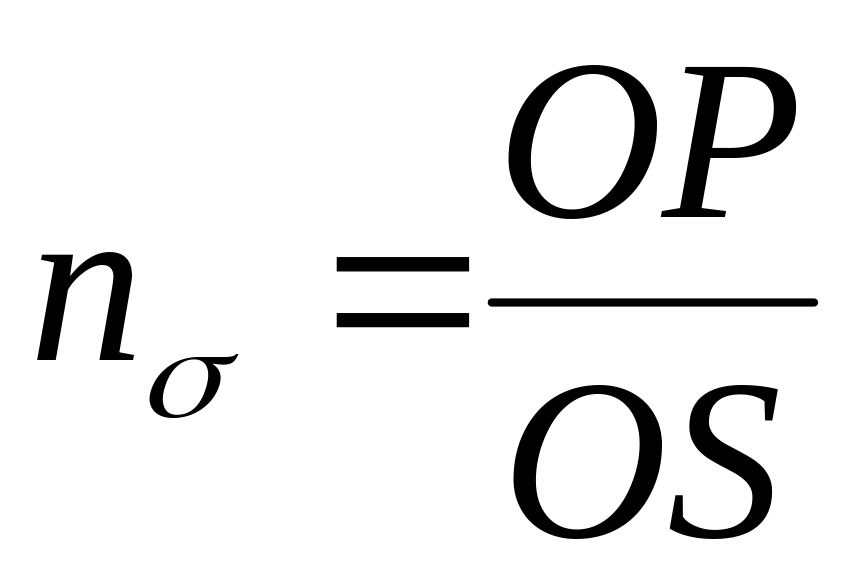9. Построение схематизированной диаграммы предельных амплитуд по касательным напряжениям проводится аналогично с той лишь разницей, что используются все механические характеристики материала и коэффициенты, влияющие на предел выносливости, по касательным напряжениям.

2. Пример расчета

Задача

Участок вала с концентратором напряжений в виде выточки подвергается совместному действию изгиба и кручения. Значение изгибающего момента изменяется в диапазоне: , , крутящего момента – в диапазоне: , . Значения геометрических размеров вала: D = 55 мм, d = 50 мм, r = 2 мм, t =  . Вал изготовлен из стали 40ХН с механическими характеристиками: , , , , _–1 = 240 МПа.

Требуется:

1. Определить характеристики циклов нормальных и касательных напряжений, возникающих в опасном сечении участка вала.

2. Определить по справочным таблицам коэффициенты, влияющие на предел выносливости по нормальным и касательным напряжениям.

3. Определить коэффициенты запаса усталостной прочности по нормальным и касательным напряжением, используя соответствующие формулы.

4. Определить коэффициенты запаса усталостной прочности по нормальным и касательным напряжением графически, построив схематизированные диаграммы предельных амплитуд, сравнить их со значениями, рассчитанными по формулам.

5. Определить коэффициент запаса усталостной прочности по формуле Гафа-Полларда и коэффициент запаса по текучести. Сделать выводы о наиболее вероятном механизме разрушения.

Решение

1. Определим характеристики циклов нормальных и касательных напряжений, возникающих в опасном сечении участка вала, которым является сечение выточки диаметром d.

Характеристики цикла нормальных напряжений:

симметричный тип цикла

;

;

; .

Характеристика цикла касательных напряжений:

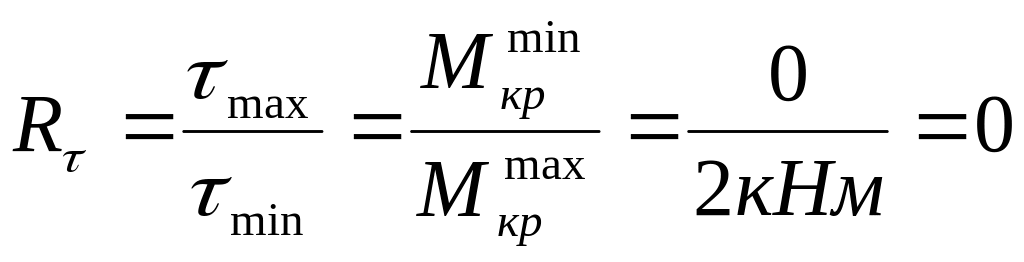отнулевой или пульсационный тип цикла;

;

;

.

2. Определим по справочным таблицам коэффициенты, влияющие на предел выносливости по нормальным и касательным напряжениям (см. Приложение 4.4, стр. 161-168).

;

3. Определим коэффициенты запаса усталостной прочности по нормальным и касательным напряжением, используя соответствующие формулы.

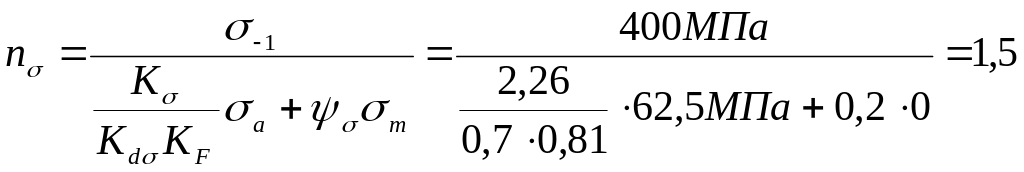
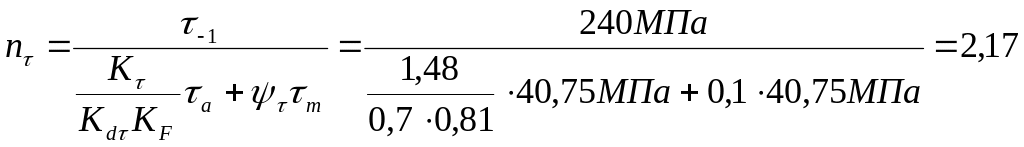
4. Определим коэффициенты запаса усталостной прочности по нормальным и касательным напряжением графически, построив схематизированные диаграммы предельных амплитуд. Сравним их со значениями, рассчитанными по формулам.

Прежде, чем строить диаграммы, определим: , тогда . Угол для диаграммы по нормальным напряжениям определим как .

,

Угол для диаграммы по касательным напряжениям определим как .

Построение диаграммы предельных амплитуд по нормальным и касательным напряжениям проведем согласно выше приведенному алгоритму.

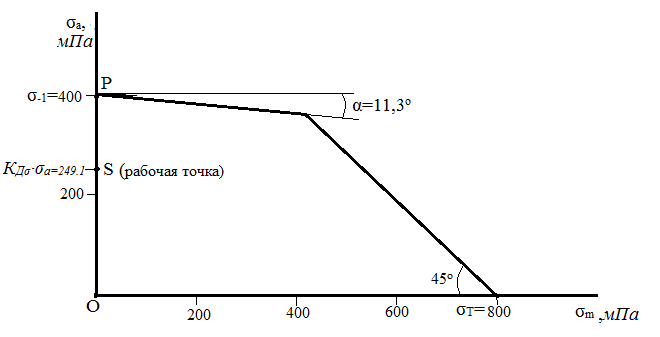
Рабочая точка S находится на оси σ_а диаграммы предельных амплитуд по нормальным напряжениям, т.к. цикл нормальных напряжений симметричный. Коэффициент запаса усталостной прочности определим, замерив отрезки ОР и OS: .

Аналогично строим диаграмму предельных амплитуд по касательным напряжениям.

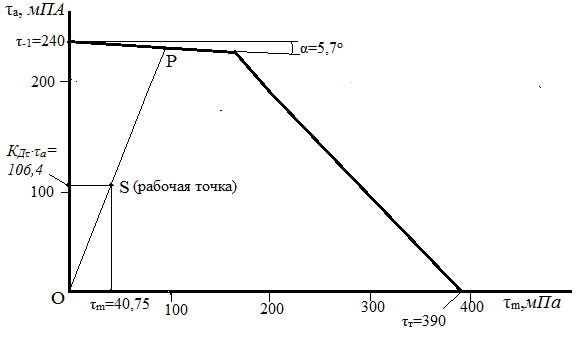
Замерив отрезки ОР и OS, определим . Приблизительно значения коэффициентов запаса усталостной прочности, определенные по формулам и по диаграммам совпадают.

5. Определим коэффициент запаса усталостной прочности по формуле Гафа- Полларда и коэффициент запаса по текучести, на основании которых сделаем выводы о наиболее вероятном механизме разрушения.

Поскольку вал работает при повторно переменном изгибе и кручении, то оценка запаса усталостной прочности производится по формуле Гафа- Полларда:

.

Коэффициент запаса по текучести определим по формуле:

,

где – максимальное эквивалентное напряжение определим по четвертой теории предельного состояния:

, тогда

.

Сравнивая полученные коэффициенты:

,

можно сделать вывод, что в материале рассматриваемого вала при данных режимах нагружения механизм развития усталостных трещин работает интенсивнее, чем механизм развития пластической деформации.

Задача решена.