2. Пример решения задачи Задача 1

Стойка длиной ℓ=1 м с шарнирно опертыми концами и промежуточной шарнирной опорой посередине сжимается силой F=20 кН.

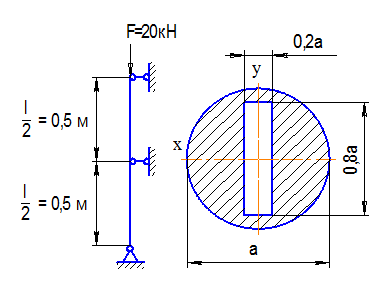
Требуется:

1. Подобрать величину размера «а» поперечного сечения стойки с использованием коэффициента продольного изгиба φ, обеспечив ее устойчивость, если допускаемое напряжение на сжатие [σ]_с=160 МПа.

2. Для спроектированной стойки определить величину критической силы и коэффициент запаса устойчивости.

Решение:

1. Определим допускаемую величину характерного размера поперечного сечения стойки.

Данная задача относится к классу проектировочных и решается методом последовательных приближений.

1. Выразим необходимые для расчета геометрические характеристики поперечного сечения через характерный размер «а». Моменты инерции:

Из этих результатов видно, что ось х является осью наименьшей жесткости и поэтому выразим через «а» радиус инерции относительно оси х:

,

где А – площадь поперечного сечения:

.

Тогда

.

2. Итерация №1. Зададим первое значение коэффициента продольного изгиба .

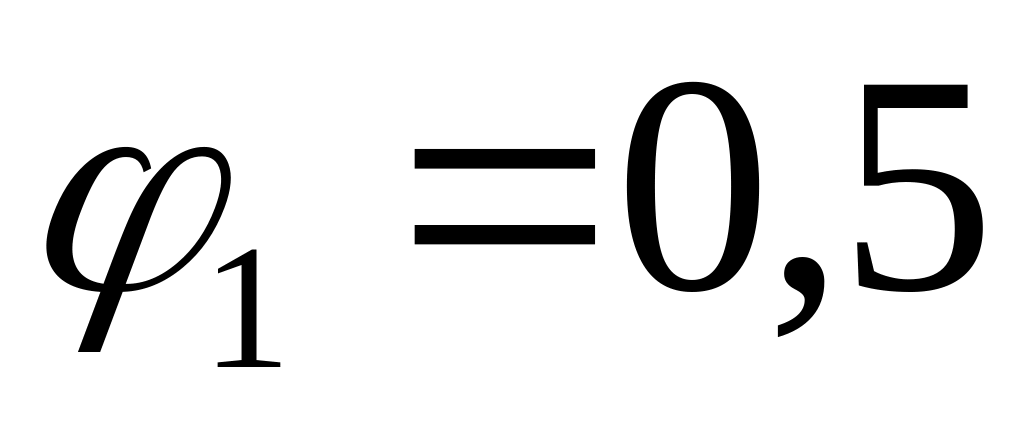3. Определим допускаемую величину площади поперечного сечения

.

4. Определим характерный размер

и минимальный радиус инерции

.

5. Определим максимальную гибкость стойки

.

6. Из таблицы коэффициента продольного изгиба по найденной гибкости и марке материала выпишем уточненный коэффициент . Полученная гибкость попала по таблице в интервал значений 90-100. Фрагмент таблицы для Ст 3:

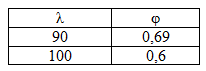
Для определения значения проведем линейную интерполяцию:

.

7. Сравним значения и , т.е. значение 0,5 и 0,6144. Расхождение в десятых долях считается существенным и составляет

,

что требует продолжения расчета (приближения). Для этого подготовим для следующей итерации коэффициент

и перейдем к расчету на второй итерации, начиная с пункта 3 алгоритма.

Итерация №2

; ;

;

.

Гибкость попала в интервал значений 100-110. Фрагмент таблицы для этого интервала:

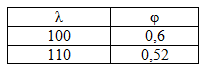
И вновь проведем линейную интерполяцию для определения :

.

Оценим % расхождения между и :

и это уже небольшое расхождение, позволяющее выйти из итерационного процесса.

8. Определим процент погрешности между расчетным (действующим) напряжением в конце 2 итерации

и допускаемым напряжением [σ]_с:

<3%,

т.е. подбор размера поперечного сечения стойки закончен.

2. Определим величину критической силы и коэффициент запаса по устойчивости.

Для определения величины критической силы узнаем, к какому типу относится данная стойка: малой, средней или большой гибкости? С этой целью сравним значение гибкости на последней итерации λ_max2=104 c предельными значениями для Ст3 λ₀=61 и λ_пред=100. Т.к. λ_max2=104> λ_пред=100 данная стойка обладает большой гибкостью, и расчет критической силы произведем по формуле Эйлера:

Коэффициент запаса по устойчивости

.

Задача решена.

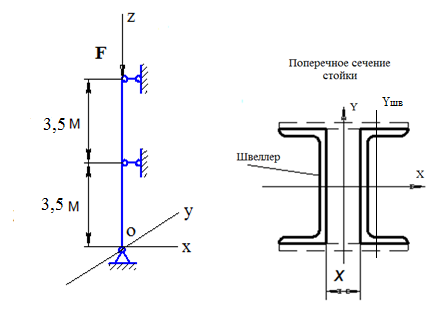
Задача №2

Стойка, имеющая поперечное сечение в виде двух швеллеров № 12, нагружена осевой сжимающей нагрузкой F. Материал стойки Ст. 2 с . Условия закрепления одинаковы в плоскостях xoz и yoz.

Требуется определить:

1. Расстояние «X» между ветвями стойки, обеспечивающее равноустойчивость конструкции.

2. Величину допускаемой нагрузки, используя коэффициент продольного изгиба.

3. Величину критической силы и коэффициент запаса устойчивости.

Решение

1. Для определения расстояния Х, при котором стойка будет равноустойчивой, запишем условие равноустойчивости: 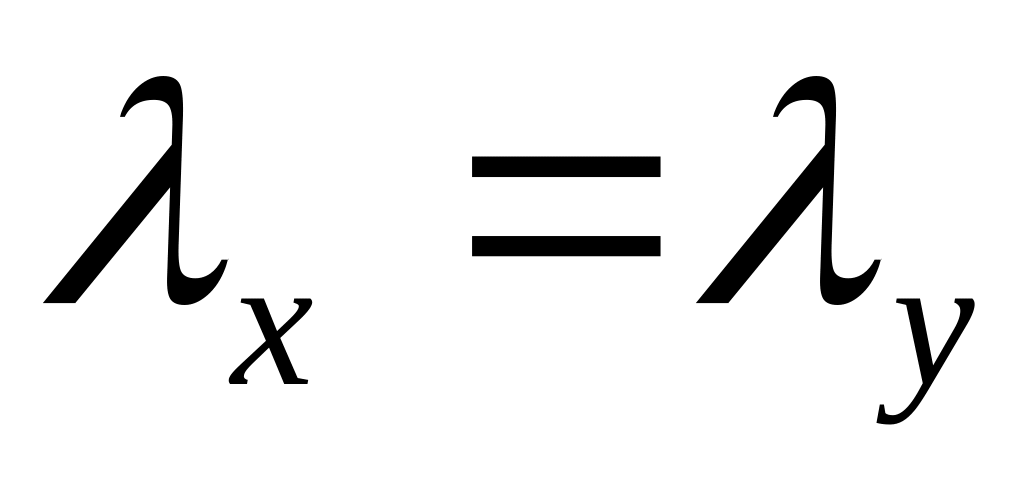. Из равенства гибкостей следует, что

,

т.е. приводит в данном случае к равенству моментов инерции. Выпишем из таблицы сортамента прокатных профилей моменты инерции швеллера №12 относительно его главных центральных осей, площадь и расстояние х_о:

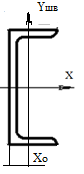
=304 см⁴, =31,2 см⁴, А_шв=13,3 см² х₀=1,54 см.

Т.к. ось Y_шв отстоит от оси Y на расстояние , то момент инерции

.

Из условия равноустойчивости определим расстояние Х:

.

2. Определим величину допускаемой нагрузки. Для этого вычислим гибкость стойки. Т.к. конструкция равноустойчива, то 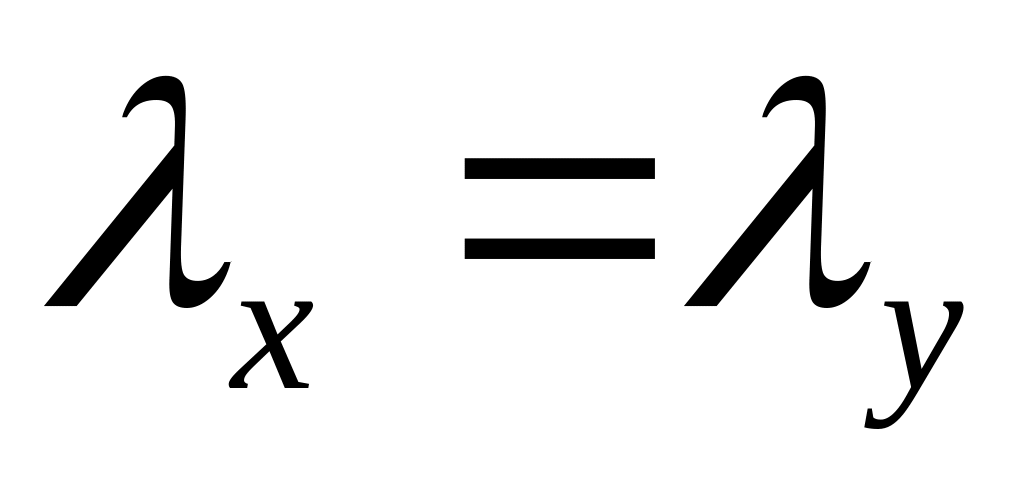. Определим 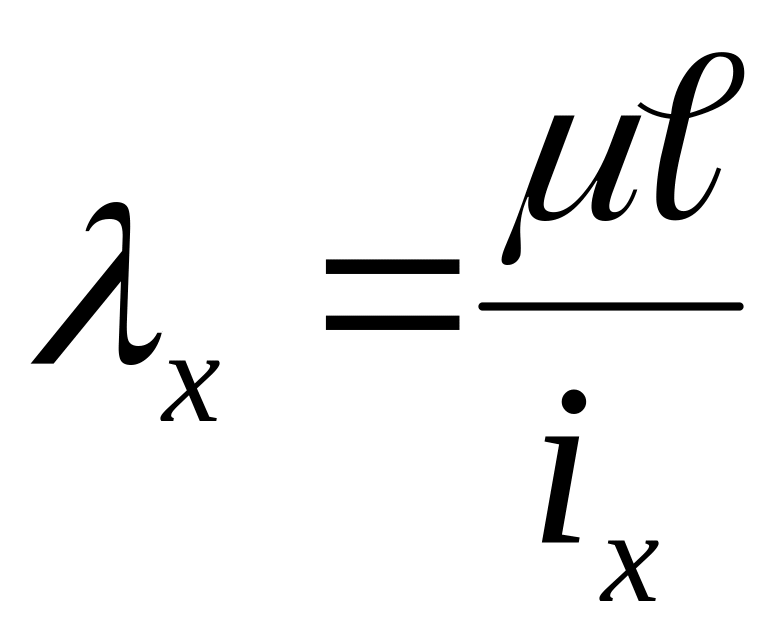, где 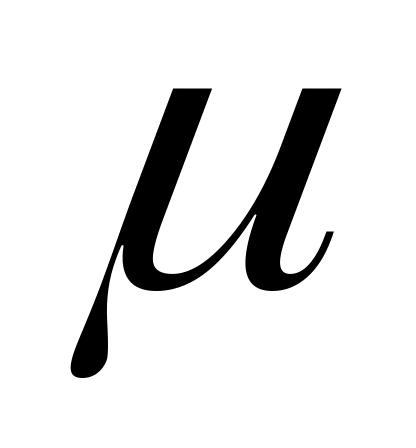– коэффициент приведения длины. Для данных условий закрепления =0,5. Радиус инерции из таблицы сортамента для швеллера №12 равен: 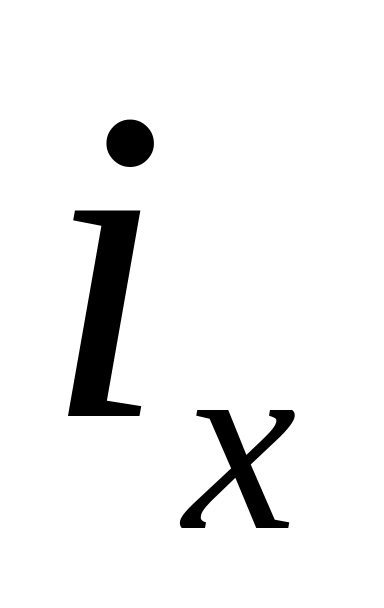=4,78 см. Тогда

.

По таблице коэффициента продольного изгиба определим величину φ в соответствии с гибкостью и маркой материала. Гибкость попала в интервал значений 70-80. Фрагмент таблицы для этого интервала:

70	0,81
80	0,75

Определим коэффициент для значения гибкости путем линейной интерполяции:

.

Применим формулу для вычисления допускаемой нагрузки:

.

3. Определим величину критической силы. Для этого из справочника выпишем значения λ₀ и λ_пред для Ст. 2: λ₀=60, λ_пред=105. Гибкость стойки , т.е. попала в интервал между λ₀ и λ_пред и относится к стойкам средней гибкости. Величина критической силы рассчитывается по формуле Ясинского:

.

Коэффициенты a и b справочные величины. Для Ст.2 , . Тогда

.

Определим коэффициент запаса устойчивости:

.

Задача решена.