3.1. Расчет на прочность для элемента II (bc)

3.1.1. Определяем положение опасного сечения.

Так же, как и в случае стержня круглого сечения, опасным является сечение C, поскольку здесь максимальны значения изгибающих моментов M_x и M_y.

3.1.2. Определяем положение опасных точек в опасном сечении.

Найдем опасные точки от действия изгиба. Для этого в плоскости сечения отложим ординаты внутренних изгибающих моментов M_x и M_y и установим положение силовой линии. Силовая линия совпадает с ординатой суммарного момента M_Σ. Опасными от изгиба будут вершины прямоугольника e и f, находящиеся в тех четвертях, через которые проходит силовая линия.

По положению ординаты суммарного изгибающего момента определяем, что в точке f возникает напряжение растяжения, ставим рядом с ней два знака «+». Точка e испытывает напряжение сжатия, и около неё ставим два знака «–». Добавив к каждой группе знаков знак «+» от действия растягивающей продольной силы N, видим, что более опасной является точка f.

Проставим также векторы касательных напряжений в точках по серединам сторон прямоугольника. Они направлены вдоль контура сечения по часовой стрелке относительно его центра (так же, как и крутящий момент M_z). Из этих четырех точек выберем для расчета две, находящиеся в той же четверти, что и точка f (точки m и n).

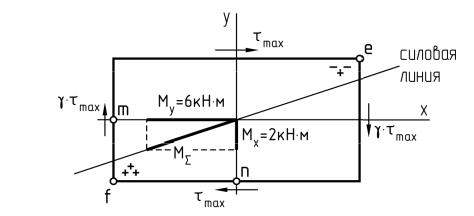
Опасной является одна из трех точек: f, m или n.

3.1.3. Составляем и решаем условие прочности.

Найдем расчетные напряжения в опасных точках, пренебрегая влиянием продольной силы N.

В угловой точке f:

, .

Точка n лежит на оси y, поэтому нормальное напряжение в ней возникает только от действия момента M_x:

.

Касательное напряжение в точке n является максимальным, так как она находится посередине длинной стороны сечения:

.

Эквивалентное напряжение для точки n (по IV теории предельного состояния):

.

В точке m нормальное напряжение определяется только моментом M_y (поскольку она лежит на оси x), а касательное напряжение равно произведению τ_max на коэффициент  (в силу того, что эта точка находится посередине короткой стороны сечения):

, .

Эквивалентное напряжение для точки m:

.

В условие прочности подставляем большее из рассчитанных напряжений:

,

откуда находим минимально необходимые размеры сечения:

,

.

Опасной является точка с максимальным расчетным напряжением – точка n. Выполняем для нее проверку на прочность с учетом продольной силы N.

,

,

.

Полученное значение меньше допускаемого напряжения [] = 160 МПа, так что условие прочности выполняется.

3.2. Проверка на прочность для элемента I (ab)

3.2.1. Для данного элемента опасным является сечение B. Вид деформации – косой изгиб.

3.2.2. Изображаем схему сечения. От его центра тяжести откладываем в масштабе ординаты изгибающих моментов M_x и M_y в тех же направлениях, что и на эпюре для сечения B. Геометрическая сумма этих ординат дает ординату суммарного изгибающего момента, продлевая которую получим силовую линию. Так как продольная сила N для элемента I отсутствует, опасными являются угловые точки в четвертях, через которые проходит силовая линия. Это точки u и v.

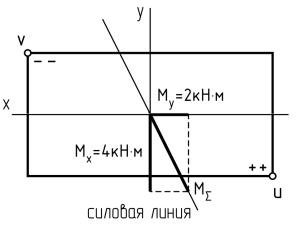
3.2.3. Вычисляем величину напряжения в опасных точках:

.

Это меньше, чем допускаемое напряжение [] = 160 МПа, то есть условие прочности выполняется.

4. Сравним стержни круглого и прямоугольного сечения по металлозатратам. Для этого определим площади сечений:

,

,

то есть в данном случае прямоугольное сечение, обладая меньшей площадью, является более эффективным с точки зрения расхода материала.

Задача решена.

Что делать, если условие прочности в пункте 2.2.3 или 3.2.3 не выполняется?

В этом случае размеры сечения (d или b и h) нужно увеличить в раз и повторить проверку.