2.1. Расчет на прочность для элемента II (bc)

2.1.1. Определяем положение опасного сечения.

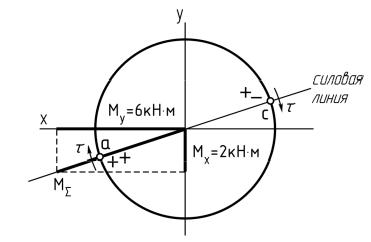
Из эпюр изгибающих моментов видно, что для элемента II наибольшие значения моментов M_x (2 кН·м) и M_y (6 кН·м) возникают в одном и том же сечении – сечении C. Оно и является опасным.

2.1.2. Определяем положение опасной точки в опасном сечении.

Сначала найдем положение силовой линии в опасном сечении. Для этого изобразим сечение и от его центра отложим ординаты изгибающих моментов M_x и M_y с соблюдением масштаба и в ту же сторону, что и на эпюрах. Геометрическая сумма ординат M_x и M_y дает ординату суммарного изгибающего момента M_Σ, которая и определяет положение силовой линии.

Опасными от действия изгиба будут точки пересечения силовой линии с контуром круга a и c. То, что ордината M_Σ отложена в сторону точки а, означает, что эта точка испытывает напряжение растяжения. Ставим рядом с ней знак «+». Противоположная ей точка с испытывает напряжение сжатия, и рядом с ней ставим знак «–».

Добавим около каждой точки по знаку «+» от действия растягивающей продольной силы N. В точке a получаем два знака «+», исходя из чего делаем вывод, что эта точка опаснее, чем точка c.

Поскольку возникающие от крутящего момента M_z касательные напряжения τ в точках a и c одинаковы, именно точка a и является опасной при совместном действии изгиба с растяжением и кручением.

2.1.3. Составляем и решаем условие прочности для опасной точки.

По теореме Пифагора вычисляем величину суммарного изгибающего момента:

.

Определяем напряжения в опасной точке, пренебрегая влиянием продольной силы N:

;

.

Чтобы оценить степень опасности состояния материала в точке a, вычисляем эквивалентное напряжение. Так как сталь Ст3 является пластичным материалом, то следует выбрать III или IV теорию предельного состояния. Воспользуемся более точной IV теорией:

.

Из условия прочности: – выражаем и вычисляем минимально необходимое значение диаметра сечения:

.

Выполним проверку на прочность для опасной точки с учетом продольной силы N:

,

,

.

Это больше, чем допускаемое напряжение [] = 160 МПа. Перегруз составляет , что не превышает 5%. Такой перегруз считается допустимым, и увеличивать диаметр сечения нет необходимости.

2.2. Проверка на прочность для элемента I (ab)

Проверим, можно ли использовать для элемента I сечение, подобранное для элемента II.

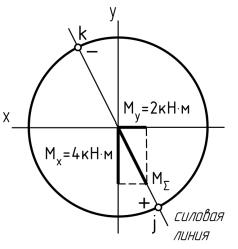
2.2.1. Из эпюр внутренних силовых факторов видно, что опасным для элемента I является сечение B, испытывающее прямой пространственный изгиб.

2.2.2. В плоскости круглого сечения откладываем ординаты изгибающих моментов M_x и M_y для сечения B по тем же направлениям, что и на эпюре. Вдоль ординаты суммарного момента проводим силовую линию. Так как для элемента I продольная сила N отсутствует, опасными являются точки пересечения силовой линии с контуром сечения j и k.

2.2.3. Вычисляем величину напряжения в опасных точках:

.

Это меньше, чем допускаемое напряжение, так что увеличивать размеры сечения не нужно.

3. Определение размеров прямоугольного сечения.

Определим предварительно рациональное расположение сечения и его геометрические характеристики.

Наибольший изгибающий момент для рамы в целом возникает на элементе II (6 кН·м). Ордината этого момента отложена на эпюре вдоль оси x элемента II, поэтому выгодно расположить прямоугольное сечение таким образом, чтобы его длинные стороны были параллельны этой оси (большей стороной вдоль большего изгибающего момента).

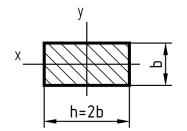
Выразим геометрические характеристики сечения через его характерный размер b. Так как , то площадь сечения , а осевые моменты сопротивления для выбранного расположения сечения:

;

.

По таблице Приложения 4.2 (стр. 159) определяем значения коэффициентов  и  для отношения h/b = 2:

 = 0,493,  = 0,795.

Момент сопротивления сечения при кручении .

Так же, как и в случае круглого сечения, сначала подбираем размеры сечения для элемента II, а затем проверяем, подходит ли это сечение для элемента I.