Алгоритм расчета на прочность при изгибе с кручением и растяжением-сжатием

1. Определение положения опасного сечения на элементе конструкции по эпюрам изгибающих моментов.

2. Определение положения опасных точек в опасном сечении. Для этого сначала нужно найти положение опасной точки только от действия изгиба с растяжением-сжатием (см. тему 3, алгоритм расчета на прочность, пункт 2, стр.30).

   • В случае круглого сечения именно эта точка является опасной и при добавлении кручения.

   • В случае прямоугольного сечения наряду с угловой опасной точкой необходимо рассмотреть также еще две точки, расположенные по серединам длин сторон прямоугольника в той же четверти, что и найденная угловая точка. В каждой из трех точек нужно посчитать расчетные напряжения по соответствующим формулам (4.2) – (4.8). Наиболее опасной из трех точек будет та, в которой наибольшее расчетное напряжение.

3. Запись условия прочности для опасной точки и его решение согласно поставленной задаче.

В условии прочности наибольшее расчетное напряжение, возникающее в опасной точке опасного сечения, сравнивается с допускаемым напряжением:

Полученное неравенство решается согласно поставленной задаче.

Если выполняется проектный расчет, то напряжением от продольной силы N на первом этапе пренебрегают. После определения размеров сечения выполняют проверку на прочность для опасной точки с учетом продольной силы. Если перенапряжение не превышает 5% от величины допускаемого напряжения, то принимают подобранные размеры. Если это условие не выполняется, то размеры сечения увеличивают и повторяют проверку.

4.2 Пример решения задачи

Консольная рама из двух элементов одинаковой длины (l = 2 м) нагружена пространственной системой сил. Материал рамы – сталь марки Ст3 с допускаемым напряжением [] = 160 МПа.

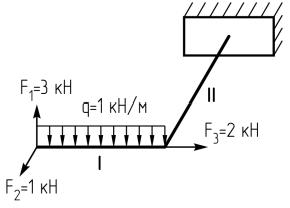
Требуется подобрать для рамы из условия прочности размеры двух видов поперечного сечения: круглого с диаметром d и прямоугольного с соотношением длин сторон h/b = 2. Определить, какое сечение является более эффективным с точки зрения расхода материала.

Решение

1. Построим эпюры продольной силы N, изгибающих M_x, M_y и крутящих моментов M_z.

Введем для каждого стержня систему координат. При этом ось z всегда направляется вдоль оси стержня, а оси x и y являются главными центральными осями поперечного сечения.

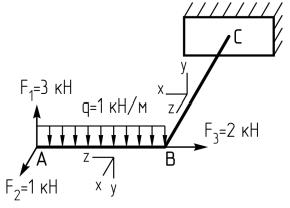
В качестве базы для построения эпюр используем конфигурацию рамы, которую вычерчиваем в любом удобном месте.

Элемент I (AB)

Продольная сила.

В начале элемента (сечение A) нет силы, действующей вдоль оси z, поэтому N = 0.

Изгибающий момент в плоскости yz.

В этой плоскости на элемент I действуют сосредоточенная сила F₁ и равномерно распределенная нагрузка q. Наличие распределенной нагрузки говорит о том, что эпюра изгибающих моментов M_x должна иметь вид параболы с выпуклостью, направленной вниз (в сторону действия нагрузки q). Строим эту параболу по двум точкам.

В начале элемента отсутствует сосредоточенный внешний момент, поэтому .

Вычисляем величину изгибающего момента в конце элемента:

(растянуты нижние волокна).

Изгибающий момент в плоскости xz.

В этой плоскости на элемент I действует сосредоточенная сила F₂. Так как распределенной нагрузки нет, эпюра изгибающих моментов M_y должна быть прямолинейной. Строим эту прямую по двум точкам.

В начале элемента отсутствует сосредоточенный внешний момент, поэтому .

Вычисляем величину изгибающего момента в конце элемента:

(растянуты задние волокна).

Крутящий момент.

На элемент I не действуют моменты относительно оси z, поэтому M_z = 0.

Элемент II (BC)

Отсечем и отбросим элемент I рамы. К оставшемуся элементу II в сечении B прикладываем силы, перенося их с элемента I (при этом распределенная нагрузка заменяется равнодействующей силой ). Кроме того, в сечении B прикладываем моменты, полученные в конце элемента I. Их величину и направление устанавливаем по эпюрам M_x и M_y. Моменты действуют в той же плоскости, в которой находится соответствующая эпюра, а их направление будет навстречу движению вдоль линии эпюры:

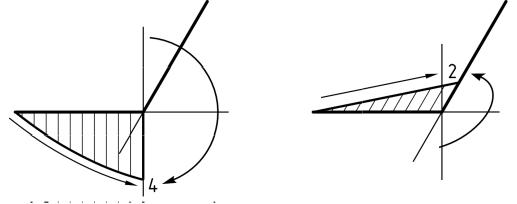
Получаем следующую расчетную схему для элемента II:

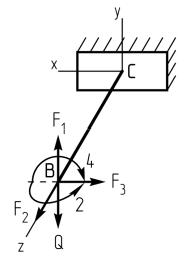
Продольная сила.

Действующая вдоль оси z сила F₂ растягивает элемент II, поэтому возникающая продольная сила положительна и равна по величине N = F₂ = 1 кН. На эпюре изображаем прямоугольник с ординатой 1 кН, откладывая ее от базы в любом направлении. В поле эпюры указываем знак «+».

Изгибающий момент в плоскости yz.

В данной плоскости на элемент II действуют сосредоточенные силы F₁ и Q. По отсутствию распределенной нагрузки определяем, что эпюра M_x должна быть прямолинейной.

В начале элемента в данной плоскости нет сосредоточенного момента, поэтому .

В конце элемента:

(растянуты нижние волокна).

Изгибающий момент в плоскости xz.

В этой плоскости на элемент II действует сосредоточенный момент 2 кН·м и сила F₃. Распределенная нагрузка отсутствует, поэтому эпюра M_y имеет вид прямой линии.

В начале элемента действует момент 2 кН·м, растягивающий левые волокна, то есть .

В конце элемента:

(растянуты левые волокна).

Крутящий момент.

Действующий по часовой стрелке относительно оси z момент 4 кН·м приводит к возникновению в поперечных сечениях элемента II крутящего момента M_z = 4 кН·м.

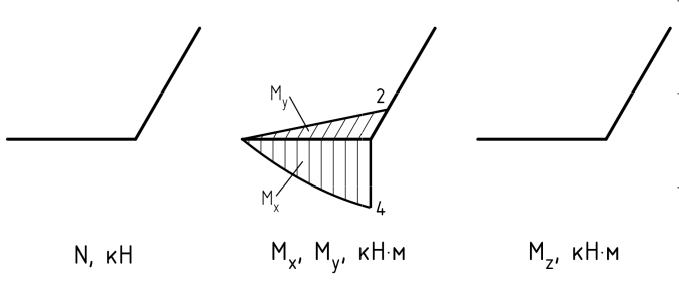
В окончательном виде эпюры внутренних силовых факторов выглядят следующим образом:

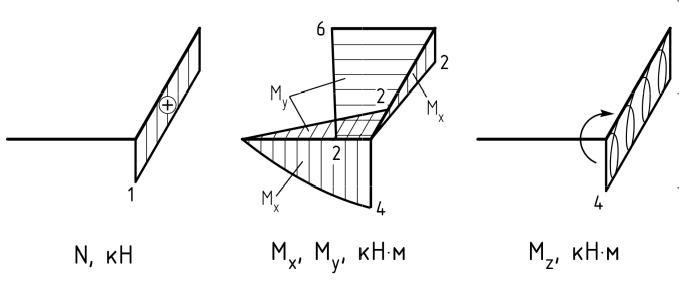
2. Определение размеров круглого сечения.

По эпюрам внутренних силовых факторов видно, что элемент II является более нагруженным по сравнению с элементом I: здесь больше величины изгибающих моментов M_x и M_y и, кроме того, имеются крутящий момент M_z и продольная сила N. Поэтому для выполнения проектного расчета выбираем элемент II.