3. Потренируемся?

• Пройти тестовый тренинг (Приложение 1, тесты к теме 3, стр. 102)

Тема 4. Расчет на прочность при изгибе с растяжением-сжатием и кручением

Цель занятия:

Научиться оценивать прочность конструкции, работающей в условиях изгиба с растяжением-сжатием и кручением.

Необходимые знания для достижения цели:

1. Особенности построения эпюр внутренних силовых факторов для рам.

2. Рациональное расположение прямоугольного сечения при изгибе.

3. Положение опасных точек в сечениях круглой и прямоугольной формы, испытывающих изгиб с кручением и растяжением-сжатием, а также формулы для расчета нормальных и касательных напряжений в этих точках.

4. Понятие эквивалентного напряжения и формулы для его определения для пластичных материалов.

5. Алгоритм расчета на прочность при изгибе с кручением и растяжением-сжатием.

1. Теоретический материал

Какие эпюры необходимы для расчета на прочность при изгибе с кручением и растяжением-сжатием?

В общем случае нагружения в поперечных сечениях конструкции возникают все шесть внутренних силовых факторов: продольная сила N, поперечные силы Q_x и Q_y, изгибающие моменты M_x и M_y, крутящий момент M_z. Однако, при расчете на прочность влиянием поперечных сил, как правило, пренебрегают. Это связано с тем, что касательные напряжения от крутящего момента обычно существенно больше, чем от поперечных сил. Таким образом, необходимость в эпюрах поперечных сил отпадает.

Как строятся эпюры для конструкций, состоящих из нескольких стержней?

Конструкции, состоящие из нескольких стержней (элементов), жестко соединенных друг с другом, называются рамами.

Для рам эпюры внутренних силовых факторов строятся, как и для балок, в направлении от одного конца конструкции к другому по участкам. При прохождении узловой точки, в которой соединяются два или более стержней, необходимо:

а) перенести с пройденного стержня внешние силовые факторы в начало следующего стержня параллельно самим себе;

б) перенести внутренние моменты, полученные в конце пройденного стержня, в начало следующего стержня. При переносе изгибающих моментов момент будет действовать в плоскости соответствующей эпюры, а его направление будет навстречу движению вдоль линии эпюры, например:

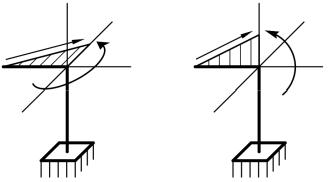
Как выбрать рациональное расположение прямоугольного поперечного сечения?

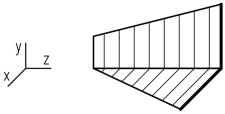
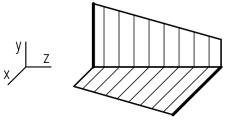
При косом изгибе возникает проблема рационального расположения сечения.

Чтобы повысить прочность элемента конструкции, целесообразно располагать его сечение таким образом, чтобы ось, относительно которой момент сопротивления наибольший, совпадала с осью, относительно которой возникает наибольший внутренний изгибающий момент для этого элемента конструкции.

Неужели нельзя объяснить по-простому?

Для прямоугольного сечения сказанное означает, что длинные стороны сечения должны быть параллельны плоскости, в которой действует наибольший внутренний изгибающий момент.

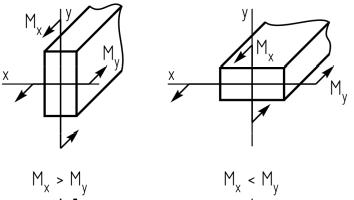
Так много эпюр! Как определить, где находится опасное сечение?

Положение опасного сечения в случае изгиба с кручением и растяжением-сжатием определяется по эпюрам изгибающих моментов M_x и M_y. Это связано с тем, что значения продольной силы N и крутящего момента M_z в большинстве случаев не меняются по длине элемента конструкции, тогда как значения изгибающих моментов обычно существенно изменяются.

Возможны два варианта изменения изгибающих моментов по длине стержня.

а) Если моменты M_x и M_y достигают максимального значения в одном и том же сечении, то именно это сечение является опасным.

б) Если максимальные значения моментов M_x и M_y приходятся на разные сечения, то при расчете на прочность нужно рассматривать оба сечения, если форма поперечного сечения прямоугольная, а для круглой формы опасным является то сечение, где максимальным является суммарный момент .

Как влияет крутящий момент на положение опасной точки в поперечном сечении? Как вычисляются напряжения в опасных точках?