15

Министерство образования и науки рф гоу впо «тверской государственный технический университет»

­­­­­­­­­­­­­­­­­

Кафедра общей физики

Р Е Ш Е Н И Е З А Д А Ч П О Ф И З И К Е

Часть 2

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ.

Методические указания для заочников

Тверь 2010

Электростатика

1. Закон Кулона определяет силу взаимодействия F между двумя точечными зарядами q₁ и q₂. Точечным зарядом называется заряженное тело, размерами и формой которого можно пренебречь по сравнению с расстояниями до других заряженных тел.

,

где r – расстояние между точечными зарядами q₁ и q₂;   –кулоновский коэффициент;  ₀ –диэлектрическая постоянная;  – относительная диэлектрическая проницаемость среды (для вакуума, воздуха, а также по умолчанию  = 1).

2. Напряженность Е – силовая характеристика электрического поля. Она зависит от вида заряженного тела, создающего поле:

− для поля, создаваемого точечным зарядом Q

,

где r – расстояние заряда до заданной точки поля;

− для поля, создаваемого равномерно заряженной бесконечной плоскостью

,

где - поверхностная плотность заряда на плоскости, ΔQ – заряд участка плоскости площадью ΔS;

− для поля, создаваемого равномерно заряженной бесконечной нитью (цилиндром)

,

где - линейная плотность заряда на нити, ΔQ – заряд участка нити длиной Δl, r – расстояние от оси нити (цилиндра) до заданной точки поля;

− для поля, создаваемого заряженной проводящей сферой радиуса R и заряда Q

,

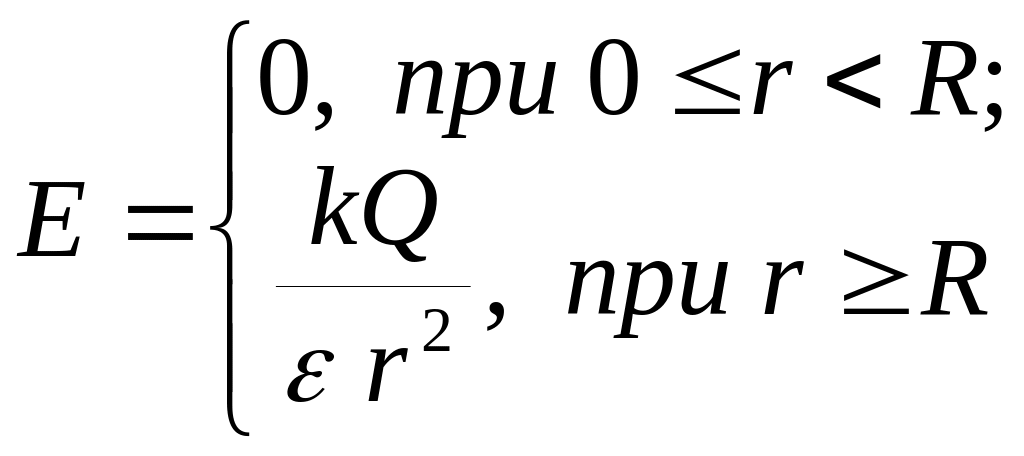где r – расстояние от центра сферы до заданной точки поля.

3. Принцип суперпозиции полей заключается в том, что если в некоторой точке пространства одновременно действует несколько электростатических полей с напряженностями и т.д., то вектор результирующей напряженности электрического поля в данной точке

Т.к. напряженности складываются векторно, то при расчетах по формуле следует учитывать направления векторов и т.д. Напряженности направлены по касательной к силовым линиям, которые идут от положительного заряда к отрицательному.

В однородном электрическом поле вектора напряженности во всех точках имеют одинаковые значения и направления.

4. Сила, действующая на пробный точечный заряд q в данной точке поля

.

5. Потенциал φ – энергетическая характеристика поля. Потенциал связан с напряженностью

,

где Е_х – проекции напряженности на ось ОХ.

Тогда

− для однородного электрического поля (например, для поля, создаваемого заряженной плоскостью)

,

где – напряжение или разность потенциалов между точками электрического поля, расстояние между которыми равно Δх;

− для поля, создаваемого точечным зарядом Q

;

− для поля, создаваемого заряженной проводящей сферой радиуса R и заряда Q

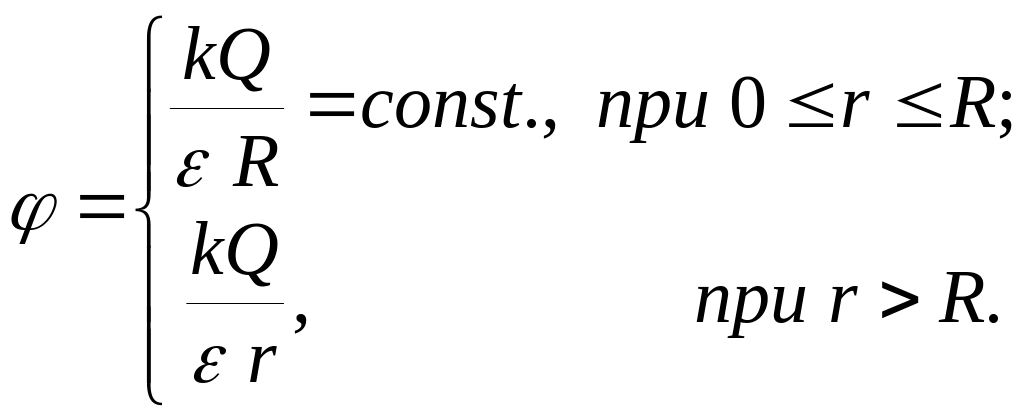
− для поля, создаваемого равномерно заряженной бесконечной нитью (цилиндром) с линейной плотностью заряда τ

.

6. Если в некоторой точке пространства одновременно действует несколько электростатических полей, то их потенциалы в данной точке складываются с учетом их знака

.

7. Потенциальная энергия пробного точечного заряда q в заданной точке поля

.

8. Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал φ₁, в другую, имеющую потенциал φ₂

.

9. С другой стороны, при совершении работы электрическое поле разгоняет заряд q, т.е. увеличивает его кинетическую энергию W_К. Тогда

,

где m – масса заряженной частицы, v₁ – скорость частицы при попадании в электрическое поле и v₂ – скорость частицы после прохождения разности потенциалов U.

Если начальная скорость частицы в электрическом поле , а конечная , то

.

Пример 1.

Расстояние между двумя положительными точечными зарядами Q₁ = 9 нКл и Q₂ = 1 нКл равно d = 8 см. На каком расстоянии от первого заряда расположена точка, в котором напряженность электростатического поля равна нулю? Чему равен потенциал поля в этой точке?

Решение:

Т .к. заряды Q₁ и Q₂ положительные, то напряженности их электрических полей в искомой точке и направлены от зарядов. По принципу суперпозиции полей результирующая напряженность в искомой точке . Очевидно, что точка в которой результирующая напряженность равна нулю должна быть расположена на прямой, соединяющей заряды, между зарядами, т. к. напряженности и будут направлены противоположно. Тогда , следовательно . Модули напряженностей полей точечных зарядов Q₁ и Q₂ равны и , где r₁ и r₂ – расстояния от зарядов Q₁ и Q₂ до искомой точки. Причем . Тогда

.

Потенциал электрического поля в данной точке , где φ₁ и φ₂ – потенциалы полей, создаваемых каждым из зарядов в отдельности. Потенциалы электрических полей точечных зарядов Q₁ и Q₂ равны и . Тогда, принимая, что и по умолчанию ε = 1, получаем

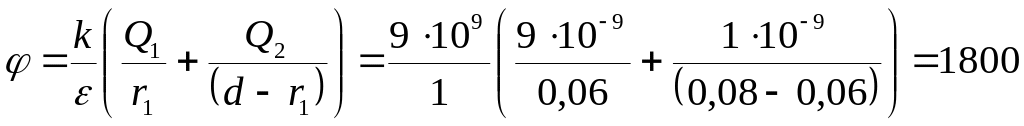 В.

Пример 2.

Электрическое поле создано бесконечной однородно заряженной плоскостью с поверхностной плотностью заряда σ = 5 мкКл/м² в среде с диэлектрической проницаемостью ε = 4. Неподвижный точеный заряд q = 2 нКл , имеющий массу m = 1 мг, под действием этого поля переместился на расстояние l = 10 см вдоль силовой линии. Определить скорость заряда в конце перемещения.

Решение:

Напряженность поля, созданного равномерно заряженной бесконечной плоскостью,

, где  Ф/м. Из формулы видно, что Е не зависит от расстояния от плоскости до заданной точки, следовательно, будет постоянной во всех точках поля и поле будет однородным. Для однородного электрического поля разность потенциалов , где - расстояние между точками с потенциалами φ₁ и φ₂.

Т.к. в начальный момент скорость заряда равна нулю , тогда  м/с.