6. Определение сил давления на плоские поверхности.

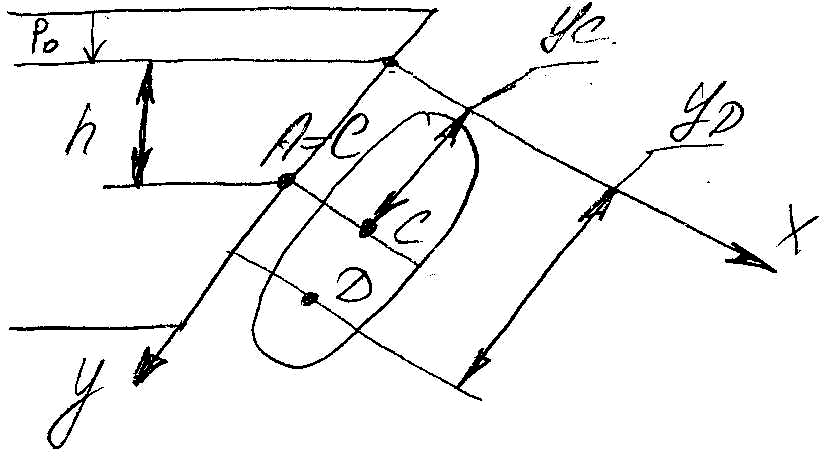
Избыточная сила гидростатического давления на плоскую стенку равна давлению в центре тяжести стенки, умноженному на её площадь.

- глубина погружения точки А или С над свободной поверхностью.

- площадь стенки.

,

1 – ое слагаемое обусловлено внешним давлением.

2 – ое слагаемое обусловлено только давлением жидкости.

Сила приложена к центру тяжести, а приложена в центре давления в точке D.

Вес жидкости налитой в сосуд может отличаться от силы давления на дно сосуда. Это явление получило название гидростатический парадокс или парадокс Паскаля.

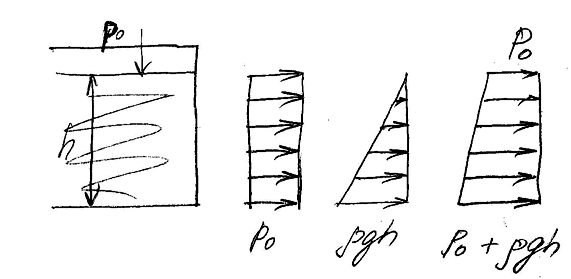
Эпюры нормального гидростатического напряжения – это графическое изображение распределения нормального гидростатического напряжения на рассматриваемой поверхности.

В общем случае точки С и D не совпадают.

Центр давления лежит ниже центра тяжести на величину .

- площадь фигуры.

- момент инерции плоской фигуры относительно центра оси, т.е. оси, проходящей через точку Ц.

Центр давления всегда совпадает для горизонтальных стенок.

Для вертикальной стенки центр давления находится на глубине

Сила давления на криволинейные стенки находится по правилу

- проекции на соответствующие оси.

10. Расход жидкости. Уравнение неразрывности потока.

Расход жидкости — объём, протекающей через поперечное сечение водотока за единицу времени. Измеряется в расходных единицах (м³/с).

Средняя скорость потока - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения

Уравнение неразрывности (сплошности) потока основано на основе сохранения массы, которое было сформулировано Ломоносовым. Базируется на положении механики сплошных сред о том, что внутри движения жидкости не может образовываться пустота или разрыв потока.

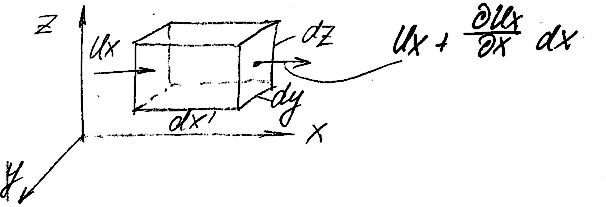
Плотность жидкости принимается постоянной, тогда масса жидкости, которая пройдет через левую грань по dt:

Через правую грань:

Закон сохранения массы требует:

- уравнение неразрывности потока в дифференциальной форме для произвольного движения несжимаемой жидкости.

Левая часть – скорость относительного изменения элементарного объема жидкости (объёмное расширение – дивергенция жидкости).

div U=0

1.Определение жидкости. Ее классификация и основные физ св-ва.

Жи́дкость — одно из агрегатных состояний вещества. Основным свойством жидкости, отличающим её от других агрегатных состояний, является способность неограниченно менять форму под действием касательных механических напряжений, даже сколь угодно малых, практически сохраняя при этом объём.

Классификация жидкостей

Структура и физические свойства жидкости зависят от химической индивидуальности составляющих их частиц и от характера и величины взаимодействия между ними. Можно выделить несколько групп жидкостей в порядке возрастания сложности.

1. Атомарные жидкости или жидкости из атомов или сферических молекул, связанных центральными ван-дер-ваальсовскими силами (жидкий аргон, жидкий метан).

2. Жидкости из двухатомных молекул, состоящих из одинаковых атомов (жидкий водород, жидкий азот). Такие молекулы обладают квадрупольным моментом.

3. Жидкие непереходные металлы (натрий, ртуть), в которых частицы (ионы) связаны дальнодействующими кулоновскими силами.

4. Жидкости, состоящие из полярных молекул, связанных диполь-дипольным взаимодействием (жидкий бромоводород).

5. Ассоциированные жидкости, или жидкости с водородными связями (вода, глицерин).

6. Жидкости, состоящие из больших молекул, для которых существенны внутренние степени свободы.

Плотность жидкости.

Если рассмотреть произвольный объем жидкости W, то он имеет массу M.

Если жидкость однородна, то есть если во всех направлениях ее свойства одинаковы, то плотность будет равна

где M – масса жидкости.

Если требуется узнать r в каждой точке А объема W, то

где D – элементарность рассматриваемых характеристик в точке А.

Сжимаемость.

Характеризуется коэффициентом объемного сжатия.

Из формулы видно, что речь идет о способности жидкостей уменьшать объем при единичном изменении давления: из-за уменьшения присутствует знак минус.

Температурное расширение.

С уть явления втом, что слой с меньшей скоростью «тормозит» соседний. В итоге появляется особое состояние жидкости, из-за межмолекулярных связей у соседних слоев. Такое состояние называют вязкостью.

Отношение динамической вязкости к плотности жидкости называется кинематической вязкостью.

Поверхностное натяжение: из-за этого свойства жидкость стремится занимать наименьший объем, например, капли в шарообразных формах.

В заключение приведем краткий список свойств жидкостей, которые рассмотрены выше.

1. Текучесть.

2. Сжимаемость.

3. Плотность.

4. Объемное сжатие.

5. Вязкость.

6. Температурное расширение.

7. Сопротивление растяжению.

8. Свойство растворять газы.

9. Поверхностное натяжение.

9. Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера)

Пусть трения не учитываются. Массовые силы давления определяются как и в гидростатике.

Разделим элементы уравнений на единицу массы жидкости

Принцип Даламбера

Силы инерции

Прибавим силы инерции к действующим силам и перенесем их в правую часть. Получим новую систему уравнений:

Уравнения Эйлера справедливы для потенциального и вихревого движения