16. Предел функции по Гейне
Значение 
называется пределом (предельным
значением)
функции 
в
точке 
,
если для любой последовательности точек 
,
сходящейся к
,
но не содержащей
в
качестве одного из своих элементов (то
есть в проколотой окрестности
),
последовательность значений
функции 
сходится
к
.[1]
Предел
функции по КошиЗначение
называется пределом (предельным
значением)
функции
в
точке
,
если для любого наперёд взятого
положительного числа 
найдётся
отвечающее ему положительное число 
такое,
что для всех аргументов
,
удовлетворяющих условию 
,
выполняется неравенство 
.[1]
Теорема
1. Если в
точке 
существуют
конечные пределы функций 
и 
,
то в этой точке существует и предел
суммы 
,
причем
.
Теорема
2. Если в
точке
существуют
пределы функций
и
,
то существует и предел произведения 
,
причем 
.
Теорема
3. Если в
точке
существуют
пределы функций
и
и
при этом 
,
то существует и предел частного 
,
причем 
.
Теорема
4. Если в
окрестности точки
выполняется
условие
и
при этом функции
и
стремятся
к одному и тому же пределу 
,
то и функция 
также
стремится к тому же пределу, т.е. 
.
17. Бесконечно малая — числовая функция или последовательность, которая стремится к нулю.
Бесконечно большая — числовая функция или последовательность, которая стремится к бесконечности определённого знака.
Бесконечно малая
Последовательность 
называется бесконечно
малой, если 
.
Например, последовательность чисел 
—
бесконечно малая.
Функция
называется бесконечно
малой в окрестности точки
,
если 
.
Функция
называется бесконечно
малой на бесконечности,
если 
либо 
.
Также
бесконечно малой является функция,
представляющая собой разность функции
и её предела, то есть если 
,
то 
, 
.
Бесконечно большая
Во
всех приведённых ниже формулах
бесконечность справа от равенства
подразумевается определённого знака
(либо «плюс», либо «минус»). То есть,
например, функция 
,
неограниченная с обеих сторон, не
является бесконечно большой при 
.
Последовательность
называется бесконечно
большой,
если 
.
Функция
называется бесконечно
большой в окрестности точки
,
если 
.
Функция
называется бесконечно
большой на бесконечности,
если 
либо 
.
Если 
,
то бесконечно малые или бесконечно
большие величины 
и 
называются эквивалентными (обозначается
как 
).
18. Замеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известныхматематических тождеств со взятием предела. Особенно известны:
Первый замечательный предел:
Второй замечательный предел:
Следствия Первый замечательный предел
Следствия Второй замечательный предел
для 
, 
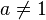
19. Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны.
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. Точки устранимого разрыва являются точками разрыва первого рода;
если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.
Теоремы
Пусть
заданы две функции 
и 
,
непрерывные на некотором множестве 
.
Сумма, произведение и частное (при
условии, что 
)
является также непрерывной функцией
на рассматриваемом множестве.
Пусть
функция 
непрерывна
в точке 
,
а функция 
непрерывна
в точке 
.
Тогда композиция этих функций 
непрерывна
в точке
.
Если
функция
является непрерывной
и строго монотонной на отрезке 
,
которые лежит на оси абсцисс, то и
обратная функция 
также
непрерывна и монотонна на некотором
отрезке 
оси
ординат.
Каждая элементарная функция, заданная в окрестности некоторой точки, непрерывна в этой точке.