7. Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Свойства скалярного произведения:

1°      - симметричность.

2°     . Обозначается   и называется скалярный квадрат.

3°    Если  , то 

4°    Если   и   и  , то  . Верно и обратное утверждение.

5°    

6°    

7°    

Векторным произведением ненулевых векторов   и   называется вектор  , обозначаемый символом   или  , длина которого  .

1°     , тогда и только тогда, когда 

2°    

3 °    Модуль векторного произведения   равен площади параллелограмма, построенного на заданных векторах   и  (рис. 2), т.е.

4°    

5°    

Смешанным произведением трех векторов  ,  ,   называется число, равное скалярному произведению вектора   на вектор  : 

1°    

2°    

3°    Три вектора компланарны тогда и только тогда, когда 

4°    Тройка векторов является правой тогда и только тогда, когда  . Если же  , то векторы  ,   и  образуют левую тройку векторов.

5°    

6°    

7°    

8°    

9°    

10°    Тождество Якоби: 

8. декартова система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Полярная система координат — двухмерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Связь между декартовыми и полярными координатами

Пару полярных координат   и   можно перевести в Декартовы координаты   и   путём применения тригонометрических функций синуса и косинуса: в то время как две декартовы координаты   и   могут быть переведены в полярную координату  :

 (по теореме Пифагора).Для определения угловой координаты   следует принять во внимание два следующие соображения:

• Для 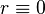 ,   может быть произвольным действительным числом.

• Для 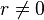 , чтобы получить уникальное значение  , следует ограничиться интервалом в 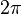 . Обычно выбирают интервал   или  .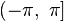

Учитывая, что для вычисления полярного угла не достаточно знать отношение   к  , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты  .

11. Каноническое уравнение эллипса.

где a>0 , b>0 — параметры эллипса. Это уравнение называется каноническим уравнением эллипса, а система координат, в которой эллипс описывается каноническим уравнением, называется канонической.Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.

Каноническое уравнение гиперболы

Перемещением центра гиперболы в начало координат и вращением её относительно центра, уравнение гиперболы можно привести к каноническому виду:

,

где a и b — полуоси

Каноническое уравнение параболы

 (или  , если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы^[1]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии  от обоих.