4. Математический аппарат исследования сау.

4.1. Математическое представление сигналов.

4.1.1.Классификация сигналов.

Сигналы являются материальными носителями информации, обуславливающей функционирование систем автоматического управления. Они делятся на регулярные (детерминированные) и случайные.

Регулярным называется сигнал, математическим представлением которого является заранее заданная функция времени. К основным типам регулярных сигналов относятся периодические, почти- периодические и непериодические сигналы.

Периодические сигналы представляются функцией времени, удовлетворяющей условию , где Т –некоторая постоянная, называемая периодом.

Почти- периодические сигналы являются функцией времени, представляемой суммой гармонических составляющих с произвольными частотами. Почти - периодические сигналы могут получиться в результате, например, сложения двух синусоид с некратными частотами.

Непериодическими называют регулярные сигналы, заданные функцией времени в пределах конечного ( ) или полубесконечного ( ) интервала времени, вне которого она тождественно равна нулю.

Случайный – это сигнал, который не может быть описан заранее заданной функции времени. Для математического представления случайных сигналов используются методы теории вероятности и статической динамики.

В технике управления применяются как непрерывные, так и дискретные сигналы. Непрерывный сигнал представляет непрерывную функцию времени. В некоторых случаях эта функция может иметь разрывы первого или второго рода, приобретая при этом конечные или бесконечные значения.

Дискретные сигналы могут быть дискретными по уровню, по времени или и по уровню, и по времени. Дискретные сигналы используются в микропроцессорных системах управления.

4.1.2.Виды задающих и возмущающих воздействий.

Внешние воздействия (возмущения) влияющие на работу САР, представляет собой непрерывные функции времени с различными законами изменения. Часто такой же характер имеют и задающие воздействия.

Заранее неизвестные законы изменения внешних воздействий затрудняют анализ статики и динамики САР. Поэтому для анализа работы систем автоматического управления часто используют так называемые типовые, управляющие и возмущающие воздействия, которые представляют собой либо наиболее вероятные, либо наиболее неблагоприятные законы изменения этих воздействий.

Широко в качестве типовых используются воздействия полиномиального вида:

(4.1)

где n=0,1,2,…- целые положительные числа; f(n)- постоянные величины;

1(t) –единичная ступенчатая функция:

при

При n=0 выражение (4.1) определяет ступенчатое воздействие:

(4.2)

При n=1 из выражения (4.1.) получим линейное воздействие (воздействие с постоянной скоростью):

(4.3)

При n=2 из выражения (4.1) получим воздействие с постоянным ускорением:

(4.4)

Графическое представление типовых воздействий соответствующих уравнениям (4.2, 4.3, 4.4) представлено на рис.4.1:

f(t)

a)

f(o)

t

f(t)

б)

t

f(t)

в)

t

Рис. 4.1. Типовые полиномиальные воздействия.

В некоторых случаях в качестве типового используется воздействие следующего вида:

(4.5)

где - дельта функция.

при

Дельта-функция (импульсный сигнал) представляет собой математическую идеализацию импульса бесконечно малой длительности, бесконечно большой амплитуды, имеющего конечную площадь, равную единице, т.е.

.

Существует математическая зависимость между единичной ступенчатой функцией 1(t) и дельта-функцией.

(4.6)

При исследовании частотных свойств элементов и систем автоматического управления широко используется гармонический (синусоидальный) сигнал. Он представляет функцию времени следующего вида:

(4.7)

где k-постоянный коэффициент; - частота; - фаза.

Следует отметить, что любое внешнее воздействие сложной формы может быть приближенно представлено в виде совокупности типовых воздействий, связанных между собой математическими зависимостями.

4.2. Статические и динамические характеристики САУ. Линеаризация.

На определенном этапе разработки и исследования автоматической системы управления получают ее математическое описание – описание процессов, проистекающих в системе, на языке математики. Математическое описание может быть аналитическим (с помощью уравнений), графическим (с помощью графиков, структурных схем, и графов) и табличным (с помощью таблиц).

Для получения математического описания системы обычно составляют описание ее отдельных элементов. В частности, для получения уравнений системы составляют уравнение для каждого входящего в нее элемента. Совокупность всех уравнений элементов и дает уравнение системы.

Уравнения (а также структурные схемы) САУ называют ее математической моделью.

Оценка качества функционирования систем автоматического управления базируется на исследовании их статических и динамических характеристик.

Статическими называются характеристики, отображающие связь между входными воздействиями и выходными координатами в установившемся режиме.

Динамическими называют характеристики, отображающие переходной процесс в системе при различных формах воздействий.

Линеаризация. Обычно автоматические системы описываются нелинейными дифференциальными уравнениями. Но во многих случаях возможна их линеаризация, т.е. замена исходных нелинейных уравнений линейными, приближенно описывающими процессы в системе. Процесс преобразования нелинейных уравнений в линейные называют линеаризацией.

Звенья и системы, которые описываются линейными уравнениями, называют соответственно линейными звеньями и линейными системами.

В зависимости от того, входит или нет время явно в уравнение, системы разделяют на стационарные и нестационарные. САУ называют стационарными, если они при постоянных внешних воздействиях описываются уравнениями, не зависящими от времени. Это значит, что свойства системы со временем не изменяются. В противном случае система называется нестационарной.

4.3. Основные свойства преобразования Лапласа.

Здесь даны основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями.

Преобразованием Лапласа называют соотношение:

(4.8)

соотношение (4.8) ставит функции x(t) вещественного переменного в соответствие функцию x(s) комплексного переменного .

При этом x(t) называется оригиналом, а x(s)- изображением или изображением по Лапласу. То, что x(t) имеет своим изображением x(s) или оригиналом x(s) является x(t), записывается (символическая форма):

(4.9)

где L- оператор Лапласа.

Соотношение

(4.10)

определяющее по известному изображению его оригинал, называют обратным преобразованием Лапласа. В нем интеграл берется вдоль любой прямой , с-число положительное.

Символически обратное преобразование Лапласа записывается следующим образом:

(4.11)

где символ L^-1-обратный оператор Лапласа.

Основные свойства преобразования Лапласа

1. Свойство линейности. Для любых постоянных и :

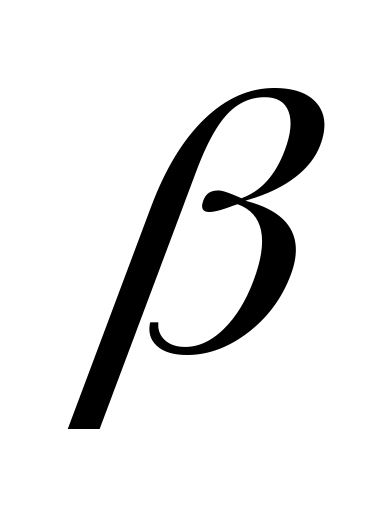(4.12)

2) Дифференцирование оригинала. Если производная является функцией – оригиналом, т.е. обладает указанными выше свойствами, то , где . Если n-я производная является функцией - оригиналом, то:

, (4.13)

где к=0,1,…,n-1.

Если начальные условия нулевые, т.е. , то последняя формула принимает вид:

(4.14)

Таким образом, при нулевых начальных условиях дифференцированию оригинала соответствует умножение изображения на s.

3) Интегрирование интеграла. Интегрирование оригинала сводиться к делению изображения на s :

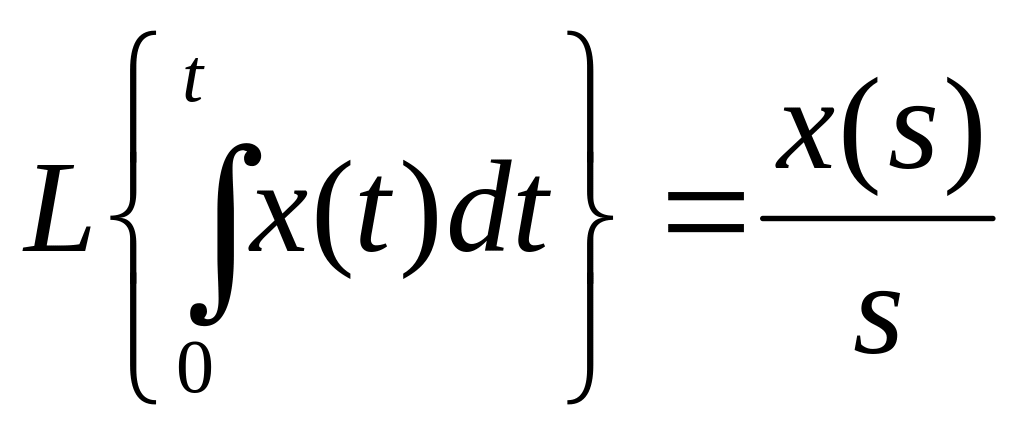(4.15)

4) Теорема запаздывания. Для любого положительного числа :

(4.16)

5) Теорема о свертке (теорема умножения изображений). Если х₁(t) и х₂(t) – оригиналы, а х₁(s) и х₂(s) – их изображения, то:

(4.17)

Интеграл правой части равенства называют сверткой функции.

6) Теорема о предельных значениях. Если х(t) -оригинал, а х(s) его изображение, то и при существовании предела :

(4.18)

7) Теорема разложения. Если функция дробно - рациональна, причем степень полинома числителя меньше степени полинома знаменателя, то ее оригиналом является умноженная на 1(t) функция:

(4.19)

где s_k – корни уравнения B(s)=0, а n_k - их кратности и l - число различных корней. Если все корни уравнения простые, то эта формула разложения принимает вид:

(4.20)

где n – степень полинома B(s),

Пример. Пусть изображение

Согласно принятому обозначению,

; ;

Функция x(s) имеет полюсы (корни уравнения B(s)=0) S₁=0, S₂= -2. Полюс S₁ является простым, а полюс S₂ - кратным, имея кратность n₂=2. Простому полюсу S₁ соответствует слагаемое

.

Кратному полюсу S₂ – слагаемое

Поэтому