8.Устойчивость линейных сау.

8.1. Понятие устойчивости.

На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

В простейшем случае понятие устойчивости системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания.

Более точно понятие устойчивости может быть сформулировано следующим образом. Линейная система автоматического управления называется устойчивой, если ее функция веса w(t) остается ограниченной при любых ограниченных по абсолютной величине входных возмущениях.

8.2.Условие устойчивости линейных САУ.

8.2.1.Впервые строгое определение устойчивости было дано русским ученым А.М. Ляпуновым в 1892г. в работе “Общая задача об устойчивости движения”. Отсутствие такого определения часто приводило к недоразумениям, т.к. движение, устойчивое в одном смысле, может оказаться неустойчивым при другом понимании этих слов, и наоборот.

При исследовании устойчивости САУ в общем случае приходится иметь дело с нелинейными задачами. Нелинейное дифференциальное уравнение может быть разложено в ряд Тейлора и представлено в виде уравнения. А. М. Ляпунов показал, что все случаи исследования устойчивости следует разделить на две категории: некритических (наиболее часто встречающихся) и критических случаев.

Для категории некритических случаев справедливы две следующие теоремы.

Теорема первая. Если вещественные части всех корней характеристического уравнения отрицательны, то система будет устойчивой независимо от членов разложения выше первого порядка.

Теорема вторая. Если среди корней характеристического уравнения найдется по меньшей мере один с положительной вещественной частью, то система будет неустойчива.

8.2.2. Алгебраическое выражение вида:

(8.1)

определяется из дифференциального уравнения, путем дифференцирования в n раз и сокращения на общий сомножитель.

Полученное алгебраическое уравнение (8.1) называют характеристическим уравнением. Его корни s₁, s₂…s_n будут определять характер переходного процесса в системе.

Так же характеристическое уравнение получают, приравнивая к нулю дифференциальный оператор при выходной величине в исходном дифференциальном уравнении, т.е.

Следует отметить, что символ p=s в характеристическом уравнении означает уже не символ дифференцирования, а некоторое комплексное число. Решение характеристического уравнения степени n содержит n корней. Корни характеристического уравнения обыкновенного дифференциального уравнения могут быть вещественными, комплексными попарно сопряженными, мнимыми попарно сопряженными, нулевыми.

В общем виде:

(8.2)

( ; ; )

Обычно корни с отрицательной вещественной частью принято называть левыми, поскольку они в комплексной плоскости расположены слева от мнимой оси, а корни с положительной вещественной частью - правыми корнями.

Определение.

Для того чтобы САУ была устойчива, необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения были отрицательны, т.е. (рис.8.1)

, (8.3)

к=1,2…n

JV JV

S₂ S₂ S₁

S₄

S₁

U S₃ U

S₅ S₃ S₅ S₂

а) САУ устойчива б) САУ неустойчива

Рис.8.1

Если хотя бы один вещественный корень или пара комплексных корней находятся на мнимой оси, а все остальные корни расположены в левой полуплоскости, САУ находится на границе устойчивости.

Различают апериодическую и колебательную границы устойчивости.

Система находится на апериодической границе устойчивости, если в характеристическом уравнении имеется хотя бы один нулевой корень. На комплексной плоскости он располагается в начале координат (рис.8.2,а). Таким образом, система оказывается устойчивой не относительно регулируемой величины y(t) ,а относительно скорости ее изменения py(t) . Сама же регулируемая величина может принимать произвольные значения. Данные системы называют нейтрально устойчивыми.

Система находится на колебательной границе устойчивости, если в характеристическом уравнении имеется хотя бы одна пара чисто мнимых корней (рис.8.2.б).

В системе при этом устанавливаются незатухающие гармонические колебания.

JV

JV

S₂ S₄ S₁

S₁

S₄ U S₃ U

S₃

S₅ S₂

а) апериодической б) колебательной

Рис. 8.2 САУ на границе устойчивости.

w w

САУ устойчива САУ неустойчива

a) б)

t t

w w САУ на границе

Колебательной устойчивости

САУ на границе

в) апериодической устойчивости г)

t

t

Рис. 8.3 К понятию устойчивости. Реакция различных САУ

на возмущение дельта-функций.

Прямой путь определения устойчивости системы состоит в отыскании корней характеристического уравнения. Однако этот путь весьма трудоемок, особенно если степень уравнения выше третьей. Поэтому, очень важно знать признаки, по которым можно судить об устойчивости САУ без непосредственного определения корней. Эти признаки называют критериями устойчивости.

Простейшим и необходимым (но недостаточным) критерием устойчивости является критерий, согласно которому необходимо, чтобы все коэффициенты характеристического уравнения были одного знака.

Для САУ описываемых дифференциальными уравнениями не выше второго порядка, необходимый критерий устойчивости одновременно является достаточным.

8.3.Алгебраические критерии устойчивости.

8.3.1. Критерий устойчивости Рауса-Гурвица.

Критерий устойчивости Рауса-Гурвица относится к алгебраическим критериям устойчивости. Этот критерий позволяет судить об устойчивости системы по коэффициентам характеристического уравнения:

(8.4)

Профессор математики Кембриджского университета Раус в 1875г. сформулировал условия устойчивости в виде таблицы. Швейцарский математик Гурвиц опубликовал в 1895г. критерий устойчивости в виде системы определителей. Оба этих критерия приводят к одним и тем же алгебраическим неравенствам и отличаются только способом их получения. Поэтому часто указанные критерии объединяют, называя критерием Рауса- Гурвица.

Рассмотрим этот критерий в форме Гурвица.

Если характеристическое уравнение системы имеет вид уравнения(8.4), причем а₀ > 0 , то для устойчивости линейной САУ необходимо и достаточно, чтобы были положительными n определителей Гурвица- 1, 2, 3…n.

Критерий устойчивости Рауса-Гурвица рационально применять для уравнений не выше пятой степени. Условие устойчивости в этих случаях имеет вид:

1. Характеристическое уравнение первой и второй степени:

Условие устойчивости: ; ;

2. Характеристическое уравнение третьей степени:

У словие устойчивости: ; ;

;

, т.е.

( ; ; ; ;

)

3. Характеристическое уравнение четвертой степени:

.

У словие устойчивости: ; ; ; ;

4. Уравнение пятого порядка:

Условие устойчивости:

Пример: Определить устойчивость САУ.

Задача 1.

,

САУ неустойчива т.к. а₁=0.

Задача 2.

САУ не устойчива т.к.

Задача 3.

Система устойчива.

Задача 4.

Дифференциальное уравнение САУ имеет вид:

Т₀=0,02с; Т₁=0,01с; Т₂=0,05с; к₀=20; к_р=0,2

Определить устойчивость методом Гурвица.

Решение: В соответствии с дифференциальным уравнением характеристическое уравнение имеет вид:

,

где ;

Так как:

а) ; ; ; ;

б) ;

;

то система устойчива

Ответ: САУ устойчива.

8.4.Частотные критерии устойчивости.

Частотные критерии устойчивости позволяют судить об устойчивости САУ по виду их частотных характеристик. Эти критерии являются графоаналитическими.

8.4.1. Критерий Михайлова.

Этот критерий устойчивости сформулирован в 1938г. Советским ученым А.В. Михайловым. Данный критерий является, по существу, геометрической интерпретацией принципа аргумента, известного из теории функции комплексного переменного и позволяет судить об устойчивости системы на основании рассмотрения некоторой кривой, называемой кривой Михайлова.

Пусть дано характеристическое уравнение системы. Левую часть характеристического уравнения называют характеристическим полиномом

Если подставить в этот полином чисто мнимое значение s=jw, то получим комплексный полином

(8.5)

Где

Выражения U(w) и V(w) соответственно вещественная и мнимая функции Михайлова.

Критерии Михайлова можно сформулировать следующим образом: для того чтобы система была устойчивой, необходимо и достаточно, чтобы кривая (годограф) Михайлова при изменении частоты w от 0 до , начинаясь при w=0 на вещественной положительной полуоси, обходила только против часовой стрелки последовательно n квадрантов координатной плоскости, где n - порядок характеристического уравнения.

На рис.8.4. показаны типичные кривые Михайлова для устойчивых систем, описываемых уравнениями, начиная от первого (n=1) и кончая пятым (n=5) порядком.

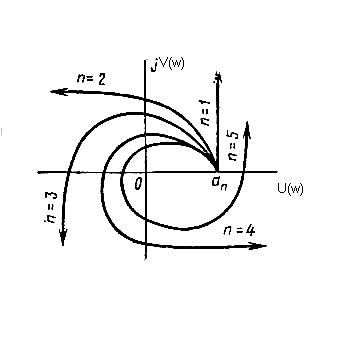
Рис.8.4

Признаком неустойчивости системы является нарушение числа и последовательности пройденных кривой Михайлова квадрантов координатной плоскости.

На рис. 8.5. показаны кривые Михайлова для неустойчивых (а, б, в, е,) и нейтральных систем (г, д):

Рис.8.5.г- система на границе апериодической устойчивости;

Рис.8.5.д- система на границе колебательной устойчивости;

небольшая деформация делает систему устойчивой (прерывистая линия)

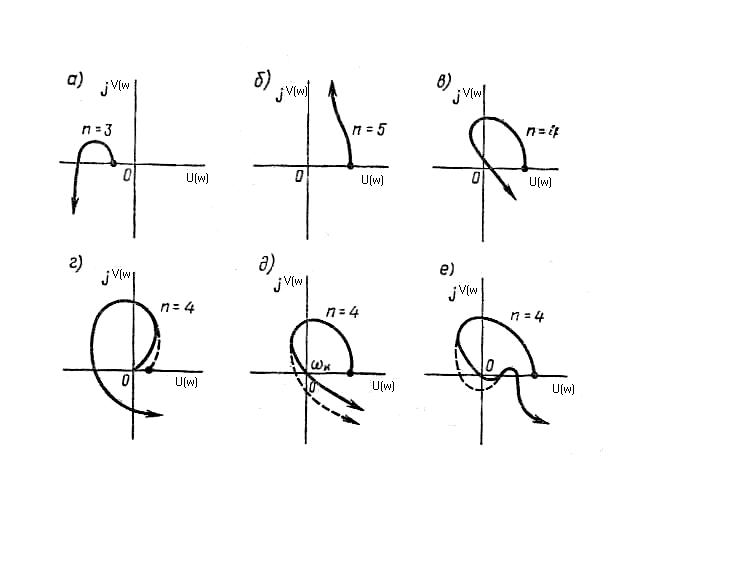
Рис.8.5

Пример: определить устойчивость САУ с помощью критерия Михайлова.

Задача 1. Характеристическое уравнение САУ имеет вид:

,

где a₀=0.04;

a₁=0.5;

a₂=2;

a₃=10.

Решение .Подставляя в левую часть характеристического уравнения p=jw и отделяя вещественную часть от мнимой, получим

Где

Задаваясь значениями , строим кривую Михайлова (рис.8.6). По виду кривой несложно сделать заключение, что система устойчива.

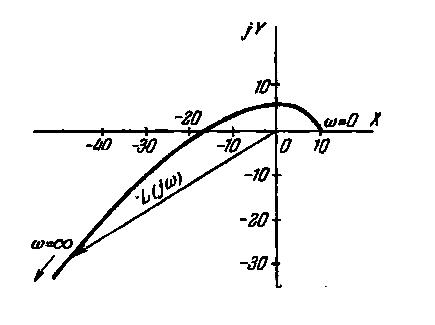
Рис.8.6 Кривая Михайлова

Задача 2. Характеристическое уравнение системы имеет вид:

Где a₀=10^-4; a₁= 4 ; a₂=0.06; a₃=1; a₄=5.

Заменив в уравнении p на jw и отделив вещественную часть от мнимой, получим

,

Где

Кривая рассчитанная по этим уравнениям приведена на рис.8.7. По виду годографа Михайлова можно судить, что система устойчива.

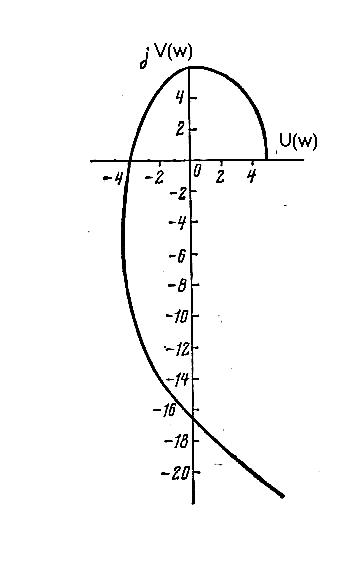
Рис.8.7.

8.4.2. Критерий устойчивости Найквиста.

Этот критерий устойчивости, разработанный в 1932г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по виду амплитудно - фазовой характеристики (АФЧХ) разомкнутой системы.

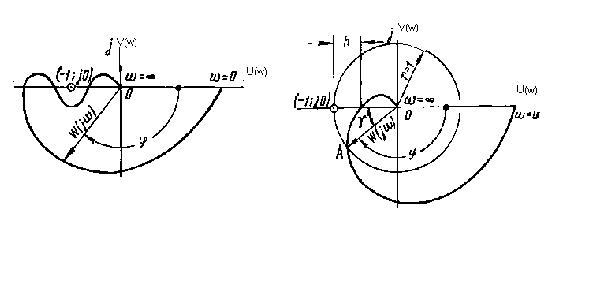
Согласно критерию Найквиста, замкнутая система будет устойчива в том случае, если устойчива разомкнутая система и ее амплитудно – фазовая характеристика (АФЧХ) не охватывает точку комплексной плоскости с координатами (-1; j0).

Кривая (рис.8.8.б) представляющая частотную характеристику устойчивой системы, пересекается с осью абсцисс справа от точки (-1; j0) и называется (АФЧХ) первого рода.

Кривая пересекающаяся с осью абсцисс и справа и слева от точки (-1; j0), называется (АФЧХ) второго рода (рис.8.8.а). В этом случае система в разомкнутом состоянии будет устойчивой при условии, если разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов(АФЧХ) через ось абсцисс слева от точки (-1; j0) равна нулю.

При анализе устойчивости системы по (АФЧХ) целесообразно ввести понятие запаса устойчивости по модулю и фазе. Если через точку (-1; j0) (рис.8.8.б) провести окружность единичного радиуса, получим точку пересечения ее с амплитудно - фазовой характеристикой (точка А). Запас устойчивости по модулю характеризуется отрезком h, а запас устойчивости по фазе - углом .

а) б)

Рис.8.8.

Пример: Определить устойчивость САУ с помощью критерия Найквиста.

Задача. Передаточная функция САУ имеет вид:

(*)

Где a₀=10^-4; a₁= 4 ; a₂=0.06; a₃=1; a₄=1; b₀=4; b₁=0.4

Заменив p=jw, можем уравнение (*) записать следующим образом:

где А= b₀ = 4;

B= b₁w = 0.4;

(формулы для разложения уравнения на вещественную и мнимую части см. в пункте 8.4.1).

Умножив числитель и знаменатель на комплексно сопряженные выражение знаменателя и отделив вещественную часть от мнимой, найдем

,

где (**)

Задаваясь значениями w , равными 0, 1, 5, 10, 15, 20 и т.д., вычисляем по уравнениям (**) величины U(w) и V(w), по которым строим АФЧХ разомкнутой системы (рис.8.9). Из графика видно, что АФЧХ не охватывает точку (-1; j0). Следовательно, система устойчива.

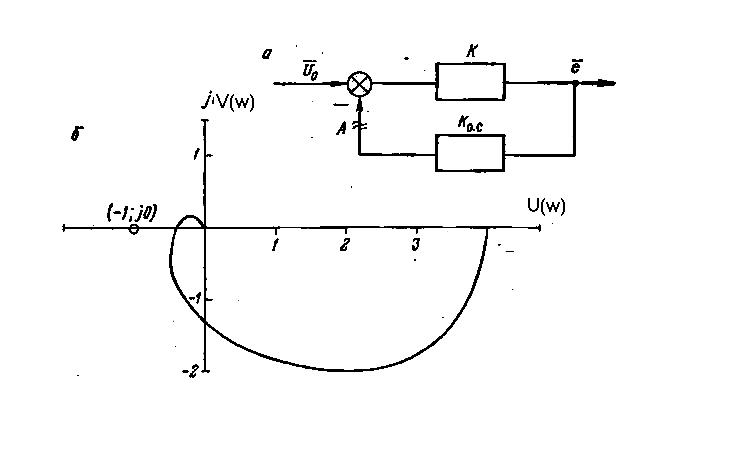
Рис.8.9

8.5 Анализ устойчивости по логарифмическим частотным характеристикам

В инженерной практике широкое применение получил анализ устойчивости САУ, основанный на применении логарифмических частотных характеристик разомкнутой системы. Это обусловлено прежде всего тем, что построение логарифмических частотных характеристик разомкнутых систем, особенно асимптотических, значительно проще, чем построение годографа амплитудно-фазовых характеристик.

Метод основывается на возможности суждения об устойчивости замкнутой САУ по взаимному расположению ЛАЧХ и ЛФЧХ системы в разомкнутом состоянии. Согласно критерию Найквиста, в случае если система устойчива, точка (-1; j0) лежит слева от АФЧХ первого рода.

При значениях аргумента характеристического вектора W(jw) разомкнутой системы и модуля система будет находиться на границе устойчивости. При этом , т.е. ЛАЧХ (рис. 8.10,а) пересекает ось абсцисс. Точка пересечения характеризуется частотой среза .

Если система устойчива, то при величине и , т.е. ордината ЛАЧХ будет иметь отрицательный знак (рис.8.10, б).

При неустойчивой системе углу соответствуют величины и . В этом случае ордината ЛАЧХ будет иметь положительное значение (рис.8.10, в).

Таким образом, при АФЧХ первого рода САУ будет устойчива в том случае, если ордината ЛАЧХ при фазовом угле имеет отрицательный знак. На рис. 8.10, б показан запас устойчивости по модулю, характеризуемый отрезком АВ, и запас устойчивости по фазе (отрезок CD).

Условие устойчивости при АФХ второго рода применительно ЛЧХ можно сформулировать следующим образом. Для того чтобы САУ, устойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии, необходимо, чтобы разность между числом положительных и отрицательных переходов фазовой характеристики через прямую ( ) при тех же значениях w, при которых ЛАЧХ L(w) неотрицательна, равнялась нулю.

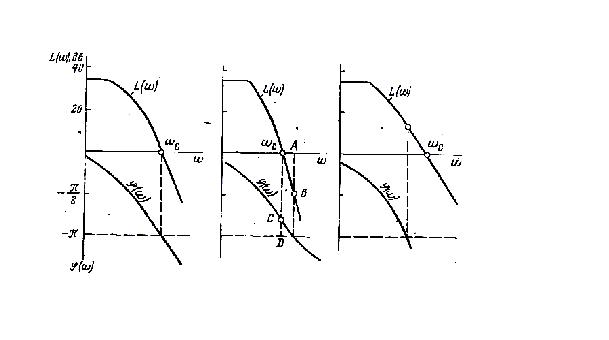
а) б) в)

Рис. 8.10

В соответствии с критерием Найквиста, САУ, не устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если разность между числами положительных переходов ЛФЧХ через прямую ( ) равна равна l/2 с учетом только тех значений w, при которых ЛАЧХ положительна. Здесь l –число корней с положительной вещественной частью.