Каноническая форма уравнений Эйлера
Рассмотрим общую задачу Лагранжа (оптимизации системы управления):
;
(3.38)
.
(3.39)
Уравнения Эйлера для функционала (3.39) имеют вид
.
Каноническая форма уравнений Эйлера является обобщением на случай оптимизации систем управления, которые относятся к задачам на условный экстремум.
Введем новые
переменные
.
Построим функцию Лагранжа следующего
вида:
.
Тогда можно рассмотреть новую задачу в виде функционала
.
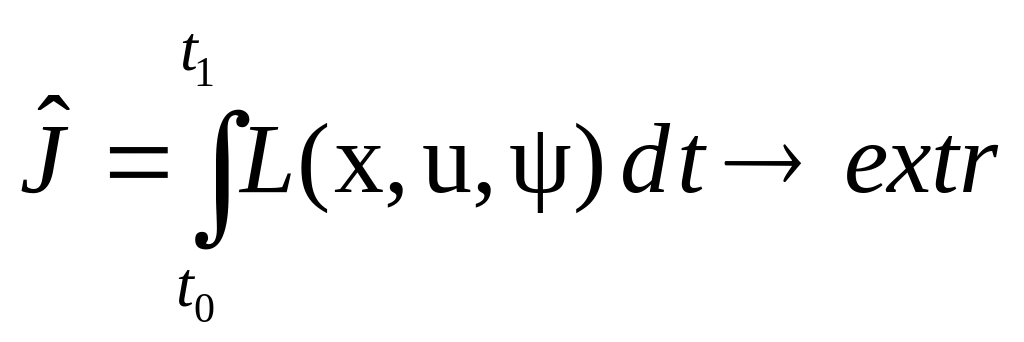Применяя уравнения Эйлера к этому функционалу, получим уравнения Эйлера в следующем виде:
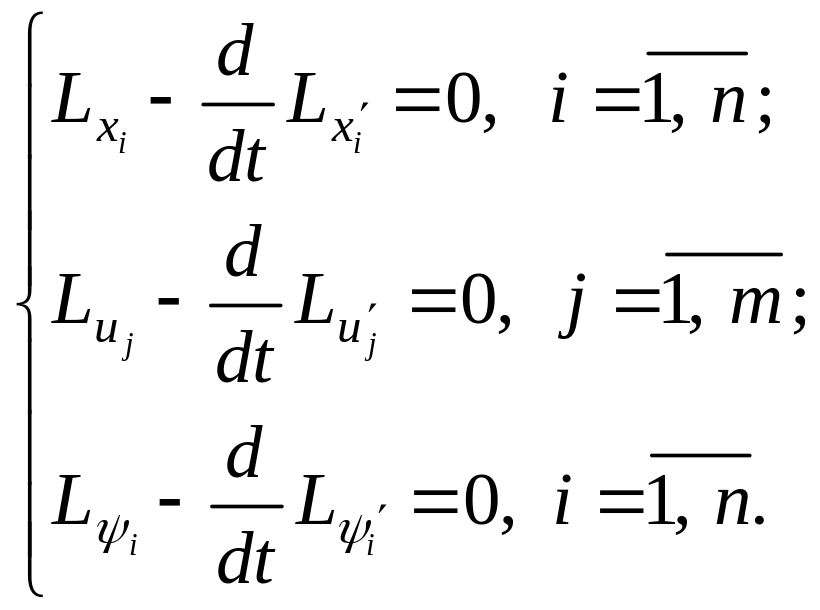
Рассмотрим каждую производную последней системы уравнений:
С учетом этих выражений уравнения Эйлера принимают следующий вид:
Эта система решается совместно с дифференциальными уравнениями связи (3.38) исходной задачи.
Введем следующие обозначения:
Тогда уравнения Эйлера можно записать в более компактной форме:
Введем новую
функцию
,
которая называется функцией Гамильтона.
Дифференцируя функцию Гамильтона по всем переменным, получим уравнения Эйлера в канонической форме:
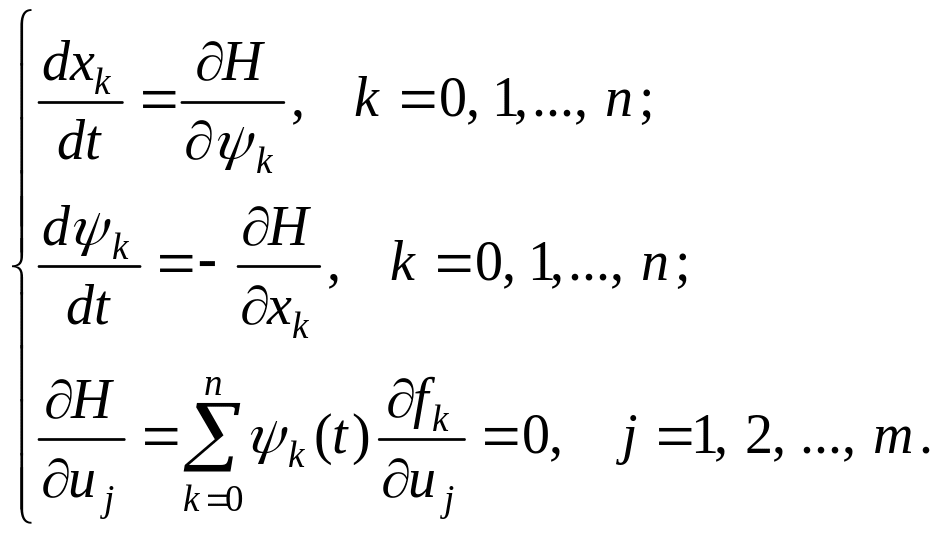(3.40)
Условие
является необходимым условием
экстремума функции Гамильтона.
Из последней
системы уравнений (3.40) определяются
переменные
– экстремали (оптимальное решение)
исходной задачи.
Применение уравнений Эйлера при ограничениях на управление
Рассмотрим линейную управляемую систему:
(3.41)
(некоторые
из коэффициентов
могут быть равны нулю), а функционалом,
экстремум которого нам надлежит
определить, является время достижения
системой положения равновесия, т. е.
,
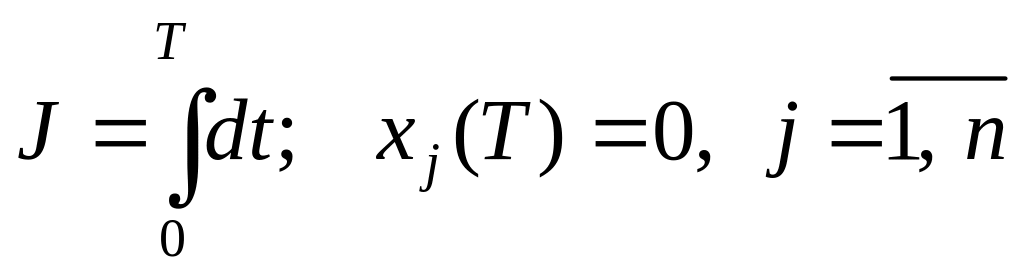и ограничения
наложены только на управление
.
Данную задачу о быстродействии сводим, согласно правилу построения функции Лагранжа, к задаче о минимуме линейного функционала
(4.42)
при граничных
условиях
;
и ограничении по модулю
.
Необходимым условием экстремума, достигаемого не на границе области, является выполнение системы уравнений Эйлера
(3.43)
Но второе уравнение в (3.43) может выполняться лишь в особом случае, когда
,
(3.44)
т.е. когда
функции
линейно зависимые, т.е. связаны между
собой линейным соотношением (3.44).
Следовательно, за исключением особого
случая, экстремалей внутри области не
существует. Следовательно, экстремум
может достигаться на границе области,
где
,
т. е. либо
,
либо
.
Поскольку в функцию Лагранжа
не входят производные
,
то, экстремум может достигаться на
разрывной функции
,
скачком переходящей от значения
к значению
и обратно (рис.3.2). Для полного определения
функции
достаточно теперь найти абсциссы точек-
разрыва
(рис.3.2).
Таким образом, функционал (3.42) на самом деле является функцией от переменных (координат точек разрыва) и можно обычными методами дифференциального исчисления искать значения доставляющие экстремум функции .
Задачу вариационного исчисления на этом можно считать решенной: мы свели ее к задаче принципиально более простой – задаче на экстремум конечного числа переменных.
Однако на практике отыскать точки разрыва методами дифференциального исчисления нелегко, особенно если учесть, что число их неизвестно.
Для их нахождения применим следующий прием: условие эквивалентно условию
(3.45)
где
.
Действительно, если
,
то
при
и интеграл стремится к бесконечности;
если же, наоборот, хотя на небольшом
участке
,
то
и значение интеграла будет меньше
.
Поэтому задача об экстремуме функционала
(3.42) при условии
эквивалентна изопериметрической задаче:
найти экстремум функционала (3.42) при
условии (3.45).
Для этой изопериметрической задачи функция Лагранжа имеет вид
,
и в качестве уравнений Эйлера получаем следующую систему уравнений:
Из уравнения (3.47) следует, что
,
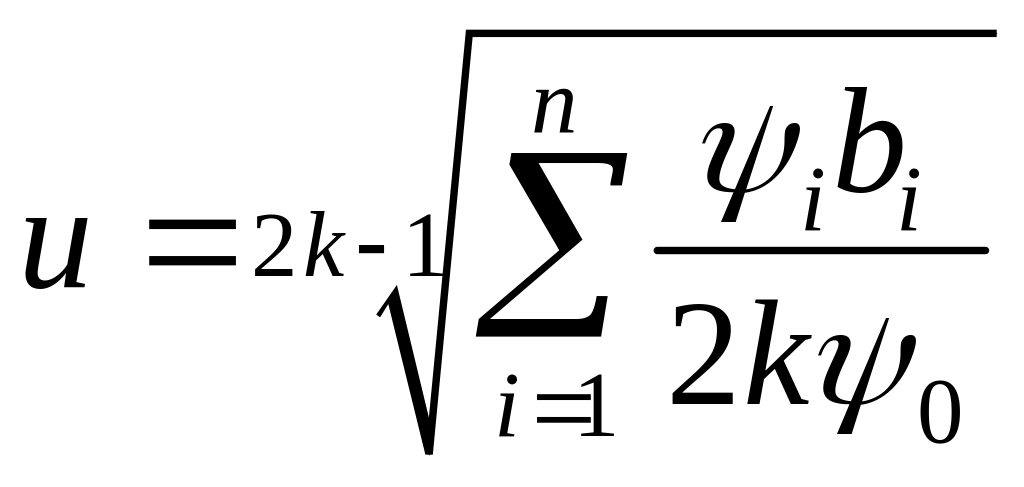но при
корень степени
из любого числа
совпадает по знаку с этим числом, т.е.
,
если
,
и
,
если
.
Символически это записывается так:
,
где символ sign
означает, что
,
если
,
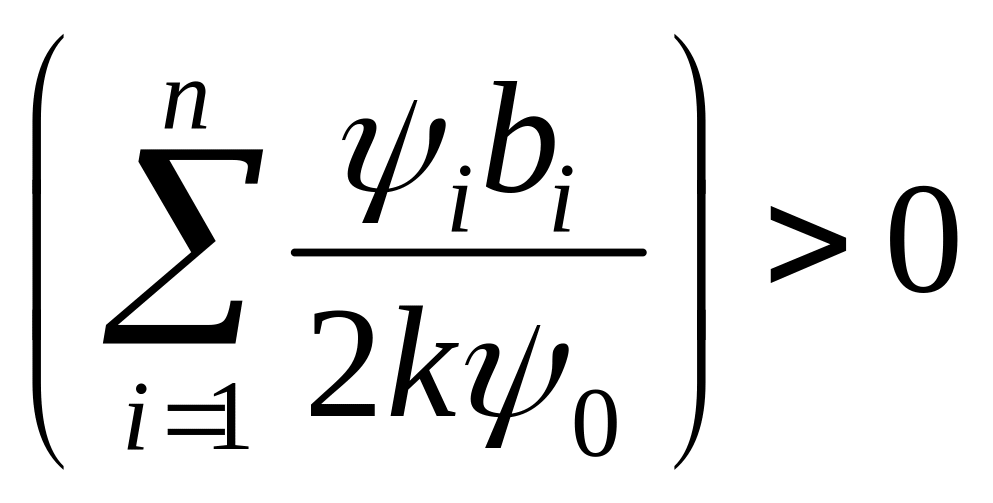и
,
если
.
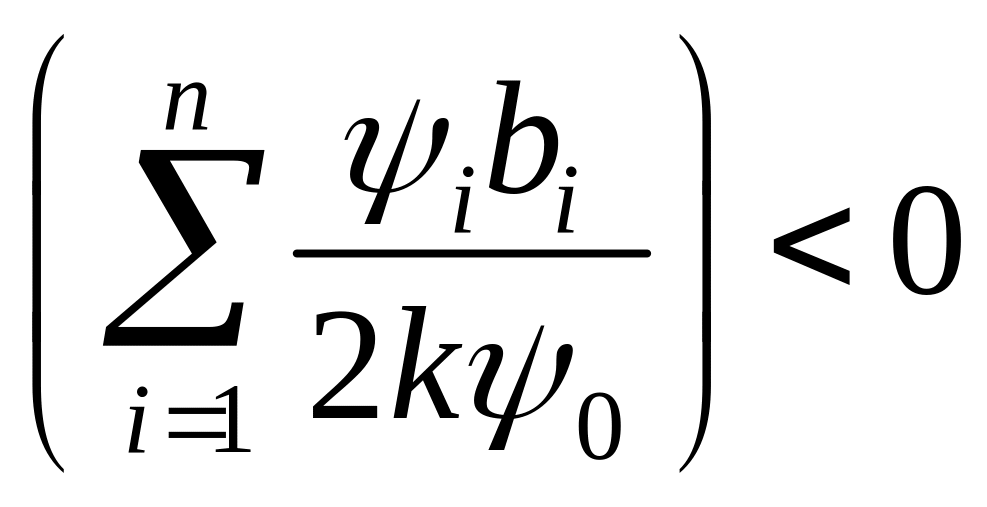Так доказывается общая теорема о числе переключений от к в линейных системах [9, с.120].
Теорема 3.1. (Об
интервалах). Для
линейной системы
–го
порядка (3.41), у которой все корни
характеристического уравнения
действительны, оптимальное по
быстродействию управление
(управление в кратчайшее время переводящее
систему из одного состояния в другое:
из
в
), будет содержать не более
переключений, т.е. не
более интервалов постоянства или .
Эта теорема используется при расчетах оптимального по быстродействию управления для линейных систем, так как позволяет свести вариационную задачу к задаче на экстремум функции переменных.