Необходимые и достаточные условия экстремума функционалов
Основной вопрос вариационного исчисления – вывод необходимых условий экстремума (для определенности – минимума).
Задача с фиксированными концами траекторий
Предположим, что на некоторой гладкой
одномерной кривой
,
проходящей через точки
и
,
достигается слабый относительный
минимум функционала
,
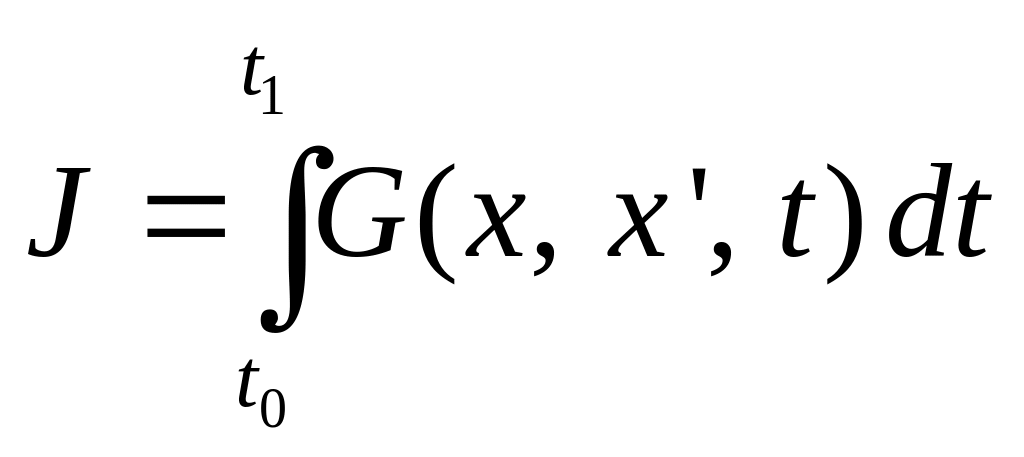(3.17)
в котором
функцию
предполагаем
непрерывной и имеющей непрерывные
частные производные по всем аргументам
до второго включительно.
Определим необходимые условия, которым должна удовлетворять функция , чтобы на ней достигался минимум функционала. Предположим, что такая функция найдена. Сравним значения функционалов для близких к функций. Близкие функции определяются малостью расстояния между самими функциями и их производными. Для функционала (3.7) должны выполняться условия близости самих функций и их первых производных.
Для сравнения
функционалов придадим функции
вариацию
,
где
,
а
–
произвольная гладкая функция,
удовлетворяющая условиям
и
,
т.е. варьируемая кривая должна проходить
через концы интервала.
Определим приращение функционала :
.
(3.18)
Разложим
в ряд Маклорена по степеням
:
,
(3.19)
где
–
остаток более высокого порядка малости
относительно первых членов разложения.
Первый член разложения (3.19) обозначается
и называется первой вариацией.
Первая вариация линейна. Второй член –
обозначается
и называется второй вариацией, она
нелинейна.
При
,
стремящемся к нулю, члены, содержащие
квадрат и более высокие степени
,
убывают быстрее, чем линейный член, и
знак приращения функционала при малых
совпадает со знаком линейного члена.
Таким образом, раскрывая производную
,
приращение
можем
представить в следующем виде:
,
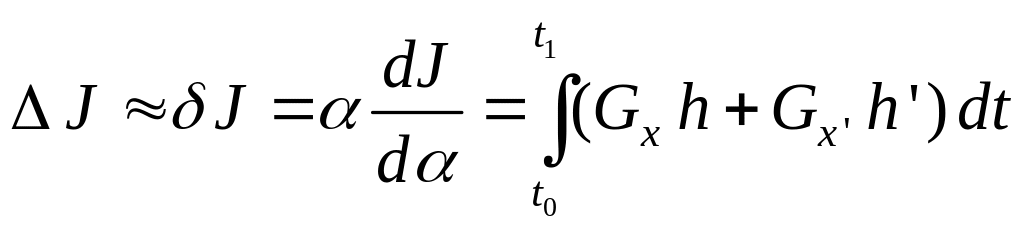(3.20)
где приняты следующие обозначения:
;
.
В то же время, согласно предположению о том, что на кривой достигается минимум функционала, разность не может быть отрицательной, т.е.
.
(3.21)
Для того, чтобы неравенство (3.21) выполнялось при любых и положительных, и отрицательных, необходимо равенство
.
(3.22)
Таким образом, необходимым условием экстремума является равенство нулю первой вариации функционала.
Проинтегрируем второй член подынтегрального выражения в (3.20) по частям:
.
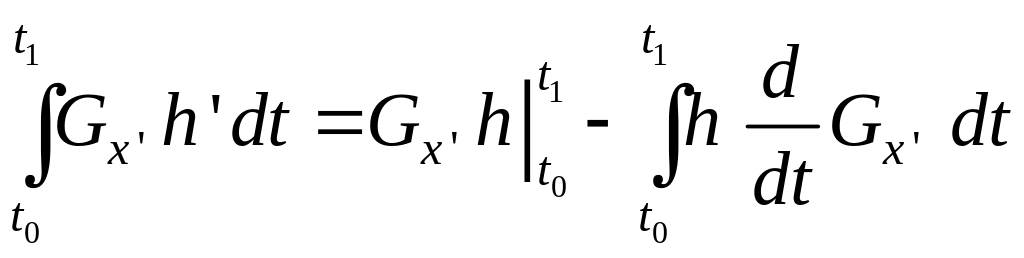Так как обращается в нуль в точках и , то
.
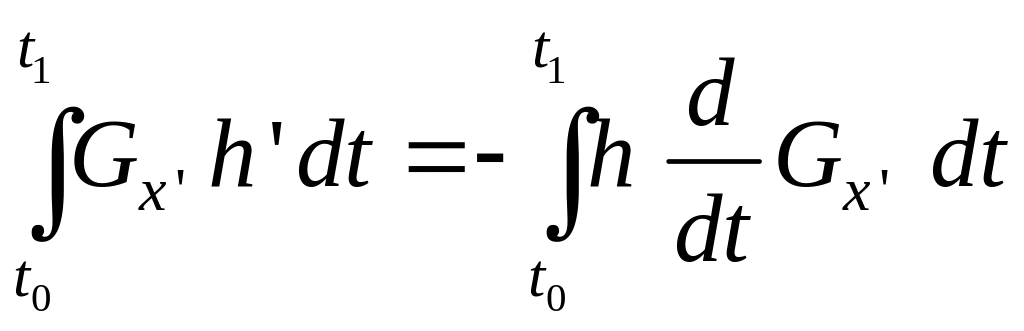В результате
.
(3.23)
Теперь к выражению (3.23) применим лемму
Лагранжа, которая утверждает: если
непрерывная функция
обладает
тем свойством, что
для любой гладкой функции
,
то обязательно
для всех
.
На основании леммы Лагранжа из равенства (3.23) можно сделать важный вывод: если доставляет экстремум функционалу (3.17), то необходимо, чтобы
.
(3.24)
Уравнение (3.24) называется уравнением
Эйлера. Оно играет центральную роль
в вариационном исчислении. С его помощью
можно фактически определить функцию,
на которой может достигаться экстремум.
Решения уравнения Эйлера называются
экстремалями. Общее решение его
содержит две неопределенные постоянные,
для определения которых требуется
удовлетворение двух условий. Как правило,
в качестве таких условий задаются
значения функции
в начале и конце интервала:
и
.
Выполнив полное дифференцирование по
второго члена уравнения (3.24) с учетом
того, что
,
получим
,
и уравнение Эйлера можно записать в следующем виде:
,
(3.25)
где
.
Из (3.25) следует, что в общем случае
уравнение Эйлера является нелинейным
дифференциальным уравнением второго
порядка и поэтому его решить нелегко.
Следует заметить, что вывод уравнения
Эйлера через лемму Лагранжа можно
считать корректным, если заранее
предполагается, что у функции
,
на которой достигается экстремум,
непрерывны как первая производная
,
так и вторая производная
.
Уравнение Эйлера можно проинтегрировать лишь в некоторых частных случаях [9, с.15–18].
В случае многомерной системы необходимыми условиями экстремума функционала
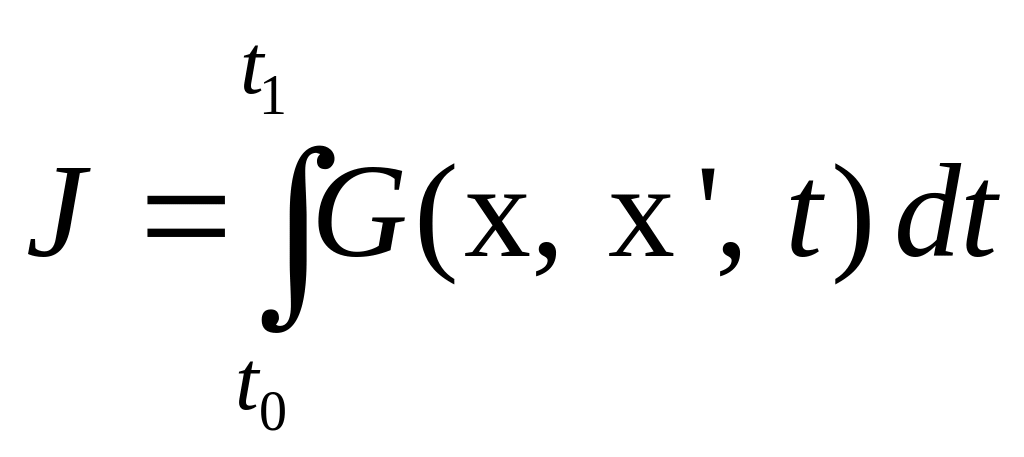
на множестве
непрерывно дифференцируемых функций
с фиксированными конечными значениями
,
при условии двойной дифференцируемости
по всем своим аргументам функции
являются уравнения Эйлера
.
Решение уравнений Эйлера (3.24) или (3.25) определяет собой возможную экстремаль функционала . Чтобы ответить на вопрос о характере экстремума на заданной экстремали, необходимо проверить выполнение достаточного условия экстремума – условия Лежандра. Это условие позволяет различать максимум и минимум.
Действительно, как показывает разложение (3.19), если первая вариация обращается в нуль, то, поскольку при достаточно малом члены высшего порядка убывают быстрее, чем квадратичный член, знак приращения функционала совпадает со знаком второй вариации:
.
Поэтому в
случае минимума
,
в случае максимума
.
Очевидно, что
.
Второй
член этого выражения можно преобразовать,
применив интегрирование по частям, с
учетом того, что
и
:
.
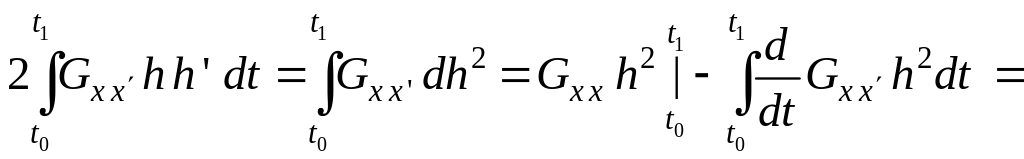
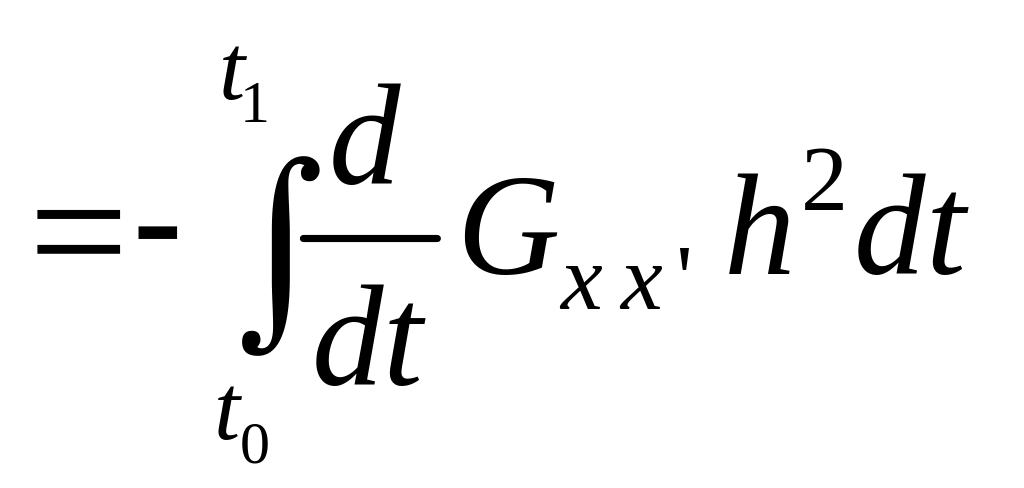Следовательно,
,
где
;
Но так как
– произвольная функция, то для того,
чтобы выполнялось неравенство
,
необходимо
.
Действительно, легко подобрать такую
функцию
,
чтобы
было мало, а
велико. Для такой функции знак второй
вариации будет совпадать со знаком
,
и мы приходим к следующему необходимому
условию (условию Лежандра):
для того,
чтобы кривая
доставляла минимум функционалу
,
должно выполняться неравенство
;
(3.26)
для максимума необходимо
.
(3.27)
Для многомерной системы достаточным условием минимума функционала, т.е. условием Лежандра, является условие положительности квадратичной формы
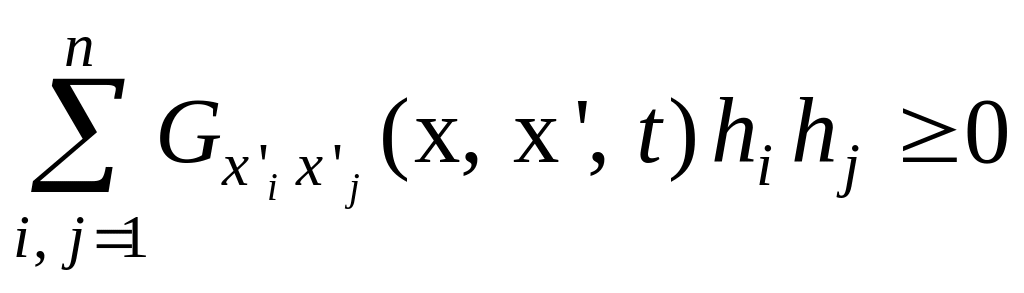при
и произвольных
.
Задача с подвижными концами траектории
Задачи с подвижными концами траектории являются более сложными. В этом случае вариация функционала зависит от вариации искомой функции и от вариации ее концов. В общем случае в качестве границ могут выступать многомерные кривые и поверхности.
Рассмотрим
одномерную задачу с функционалом (3.17)
и подвижными концами. С учетом приращения
функции
и ее концов
и
приращение функционала представим в
следующей форме:
.
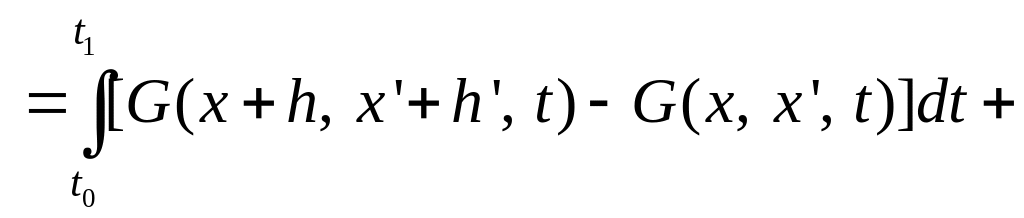
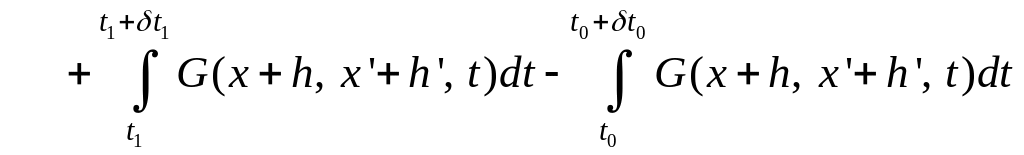Здесь первый интеграл – вариация кривой, а два последних – вариации концов.
Предположим,
что приращения
,
,
,
бесконечно малые. Тогда линейная часть
приращения функционала, т.е. первая
вариация, будет иметь следующий вид:
.
(3.28)
Второй член подынтегрального выражения в формуле (3.28) проинтегрируем по частям, в результате чего получим:
.
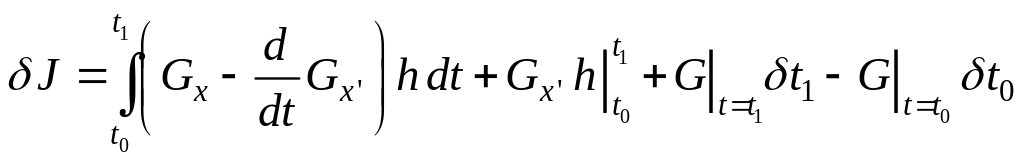С точностью до бесконечно малых высшего порядка можно написать (рис. 3.1):
;
;
и тогда окончательно получим:
(3.29)
где есть интегральный член, зависящий от вариации кривой внутри первоначального интеграла, и – члены без интеграла, зависящие от вариации концов.
Пусть,
например, требуется определить экстремум
функционала среди кривых
,
концы которых могут перемещаться по
двум кривым
и
.
Предположим, что такая экстремаль
найдена. Тогда интегральный член в
формуле (3.29) обращается в нуль и
Так как с точностью до бесконечно малых высшего порядка
;
,
то условие экстремума функционала можно записать в следующем виде:
(3.30)
Так
как
и
– независимые друг от друга приращения,
то из (3.30) следует
(3.31)
Условия (3.31) называются условиями трансверсальности. Условия трансверсальности позволяют найти положение концов экстремали.
Задача на условный экстремум
Весьма часто встречаются вариационные задачи, когда функции доставляющие экстремум функционалу, сами подчинены некоторым дополнительным условиям (уравнениям связи). Такие задачи называются задачами на условный экстремум.
Рассмотрим функционал вида
,
(3.32)
у которого
переменные (компоненты) вектора
зависимы. Характер зависимости указанных
переменных может определяться тремя
типами соотношений:
;
;
(3.33)
,
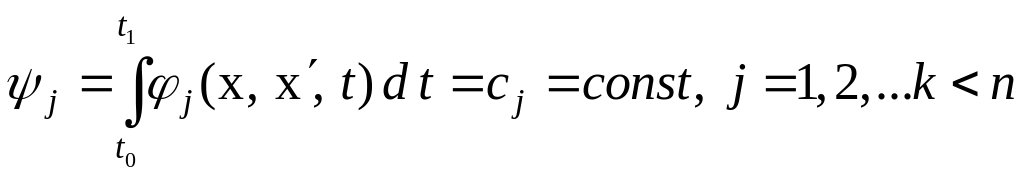называемых соответственно конечными, дифференциальными и интегральными связями. Задачу с дифференциальными связями называют общей задачей Лагранжа. К ней сводятся все другие задачи на условный экстремум.
Известно [9], что решение задачи минимизации функционала (3.32), совпадает с решением задачи на безусловный экстремум для функционала
,
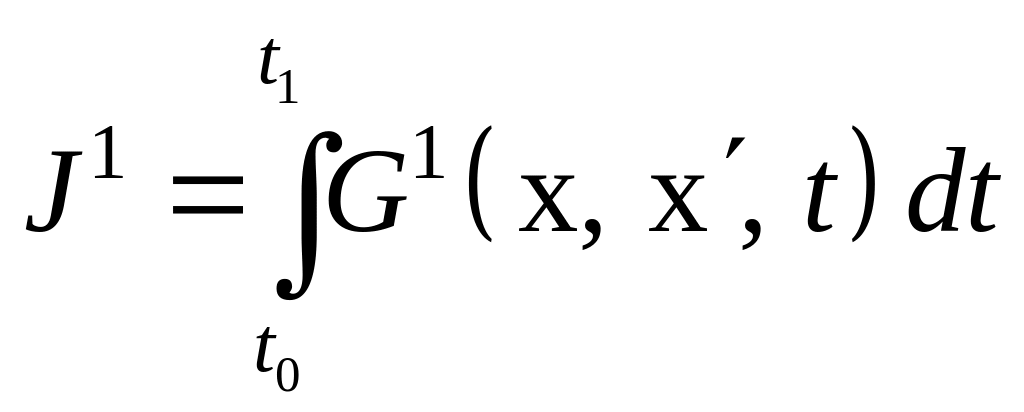(3.34)
где
– функция Лагранжа,
– неопределенные функции (неопределенные
множители Лагранжа), которые вместе
с функциями
полагаются независимыми аргументами
функционала (3.34).
Уравнения Эйлера — Лагранжа для функционала (3.34)
вместе с
уравнениями связей (3.35) образуют замкнутую
систему уравнений с неизвестными
и
.
Постоянные интегрирования общего
решения указанной системы определяются
граничными условиями
, .
Общие задачи Майера и Больца, рассматриваемые в вариационном исчислении, здесь не приводятся.