2. Критерий управляемости

В стационарном случае критерий управляемости принимает простую и компактную форму.

Пусть заданы матрицы системы и . Составим матрицу размером , первые столбцов которой совпадают со столбцами матрицы , вторые столбцов совпадают со столбцами матрицы (или просто ) и т. д., последние столбцов матрицы образованы матрицей . Матрицу записывают так:

.

Управляемость стационарной системы (2.1) связана со свойствами матрицы , поэтому называется матрицей управляемости.

Лемма 2.1. Если ранг матрицы равен рангу матрицы , то дальнейшее прибавление столбцов вида , , не увеличивает ранга матрицы.

Доказательство этой леммы можно найти в [4, с.86].

Из этой леммы, в частности, следует, что прибавление каждого последующего элемента вида либо увеличивает ранг матрицы на некоторое постоянное число, либо не меняет ранга. В последнем случае и прибавление всех последующих столбцов вида не будет увеличивать ранга матрицы.

Сформулируем теперь основной (в смысле управляемости) результат теории линейных стационарных систем.

Теорема 2.2. (критерий управляемости стационарной системы). Линейная стационарная п-мерная система (2.1) вполне управляема тогда и только тогда, когда

ранг . (2.3)

Доказательство.

Достаточность. Предположим, что ранг матрицы равен и покажем, что в этом случае вектор-функции матрицы при и линейно независимы на произвольном интервале . Иначе говоря, следует доказать, что, если ранг матрицы равен , то не существует такого постоянного вектора , что имеет место тождество

. (2.4)

Сформулированное утверждение равнозначно следующему: если существует некоторый отрезок и некоторый вектор , для которых выполняется равенство (2.4), то ранг матрицы меньше, чем .

Для доказательства последнего утверждения продифференцируем раз тождество (2.4) по переменной

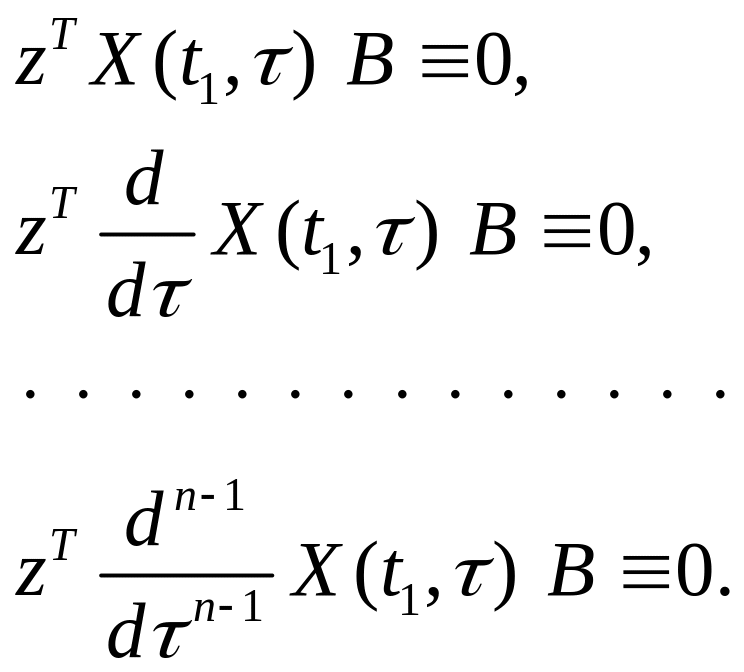(2.5)

Учитывая формулу (1.20), можем записать

,

где – обратная матрица по отношению к матрице фундаментальных решений однородного уравнения для уравнения (2.1).

Известно [4, с.62], что матрица удовлетворяет уравнению

,

а поэтому имеем

или

. (2.6)

Используя свойство (2.6), из равенств (2.5) легко получить соотношения

Положив здесь , имеем

(2.7)

Это в свою очередь возможно только в том случае, если ранг матрицы меньше .

Необходимость условий теоремы будет установлена, если докажем, что из линейной независимости вектор-функции (2.2) при на произвольном отрезке вытекает равенство ранга матрицы числу . Но это утверждение равнозначно следующему: если ранг матрицы меньше чем , то вектор-функции (2.2) при линейно зависимы на произвольном промежутке . Докажем справедливость этого утверждения.

Предположим, что ранг матрицы меньше, чем . Тогда, как известно, обязательно существует такой -мерный вектор , что

. (2.8)

Учитывая утверждение леммы 2.1, приходим к выводу, что

(2.9)

для всех целых .

Принимая во внимание, что матрицу можно изобразить степенным рядом

,

то для линейной комбинации векторов (2.4) получим выражение

.

Если в этом равенстве за вектор принять вектор, фигурирующий в равенстве (2.9), то получим

,

что означает линейную зависимость векторов (2.2).

Замечание. В случае, если вектор управления в системе (2.1) одномерный, матрица имеет вид столбца , а поэтому необходимое и достаточное условие вполне управляемости принимает форму

. (2.10)

Соотношения (2.3) и (2.10) назовем условиями вполне управляемости стационарных систем.

Определение. Система (2.1) называется вполне управляемой на заданном промежутке , если для двух произвольных значений и из фазового пространства можно указать такую функцию управления , что решение уравнения (1) удовлетворяет краевым условиям

и .

Согласно доказанной теореме 2.2 свойство управляемости системы полностью определяется алгебраическими свойствами пары матриц . Именно, если матрица , составленная указанным выше образом, имеет полный ранг, то система управляема.