3. Свойства линейных многомерных систем управления

Итак, уравнения движения линейной многомерной стационарной непрерывной системы в матричной форме имеют вид

, (1.13)

где размерности соответствующих векторов и матриц были определены в (1.1).

При исследовании многомерных систем широко используют понятие функции от матрицы, в частности, понятие матричной экспоненты , где – матрица.

Определение. Функцией называется функциональный ряд

(1.14)

Лемма 1.1. Пусть – постоянная квадратная матрица порядка , элементы которой равны действительным или комплексным числам. Тогда ряд (1.14) сходится абсолютно для всех конечных и равномерно на произвольном конечном промежутке.

Доказательство этой леммы можно найти в [4, с.58].

Определение. Матрица размером называется фундаментальной (или интегральной) матрицей системы

тогда и только тогда, когда в ее столбцах стоят линейно независимых решений этой системы.

Определитель любой фундаментальной матрицы называется определителем Вронского. Определитель Вронского не обращается в нуль ни в одной точке интервала и, следовательно, фунда-ментальная матрица при любом значении является неособенной матрицей.

Теорема 1.1. Если матрица удовлетворяет условиям леммы 1.1, то решением задачи

, (1.15)

будет матрица

(1.16)

(здесь – единичная матрица порядка ).

Доказательство. Процесс доказательства этой теоремы осуществляется непосредственной подстановкой матрицы (1.16) в уравнение (1.15) с учетом единственности решения и возможности ее дифференцирования.

Теорема 1.2. Если матрица удовлетворяет условиям леммы 1.1, то решением задачи

,

является вектор

.

Доказательство осуществляется непосредственной проверкой.

Теорема 1.3. Если матрица удовлетворяет условиям леммы 1.1, то решение задачи

, (1.17)

имеет вид

. (1.18)

Доказательство этой теоремы осуществляется непосредственной проверкой. Формула (1.18) является формулой Коши для системы (1.17).

Для определения временных характеристик систем управления важную роль игает функция , представляющая собой обычную –функцию Дирака, обладающую свойствами:

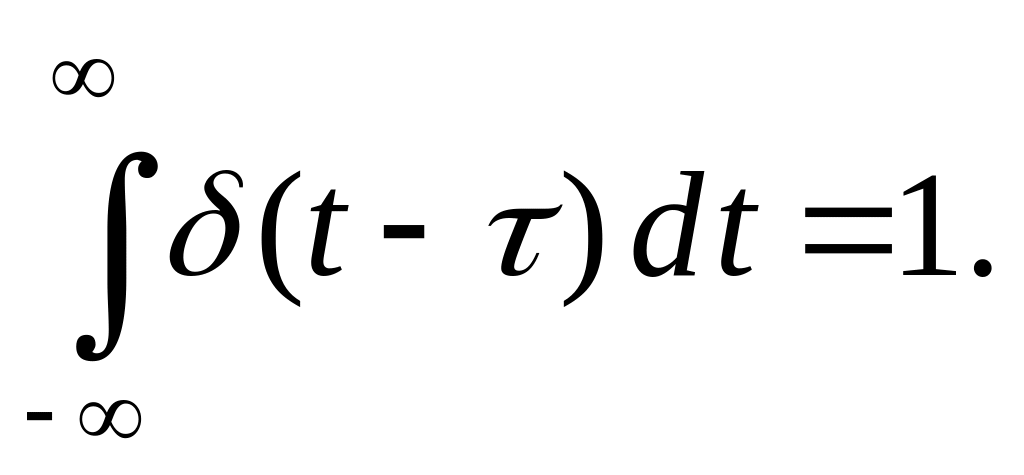
Положим в равенстве (1.18) все компоненты вектора равными нулю, за исключением одной , которую примем равной единичному импульсу , сосредоточенному в точке . Обозначим через решение (1.18) уравнения (1.17) при условии . Тогда будем иметь

,

где – единичный вектор-столбец с 1 в -ой строке.

Матрица, столбцами которой являются векторы называется импульсной переходной матрицей системы (1.17) и обозначается через .

Импульсная переходная матрица имеет вид

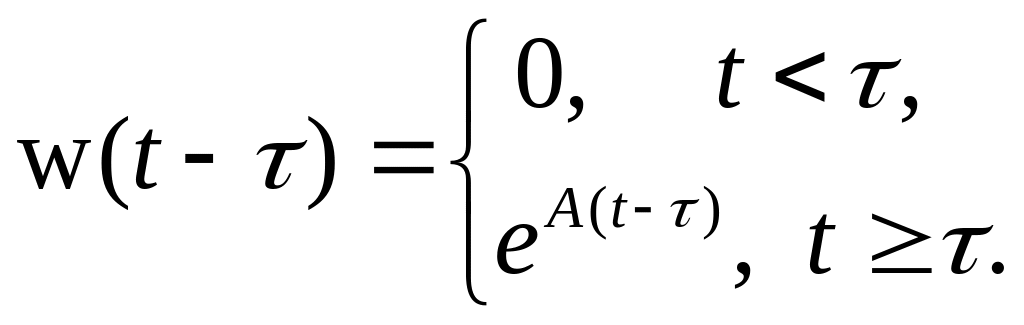
Сопоставляя матрицу с результатом теоремы 1.1, замечаем, что является решением задачи

, .

Таким образом, импульсную переходную матрицу можно представить в виде ряда экспоненты

(1.19)

С другой стороны, поскольку определитель фундаментальной матрицы не обращается в нуль ни в одной точке, то при любом фиксированном существует обратная матрица . Тогда для произвольной фундаментальной матрицы можно построить нормированную фундаментальную (или нормальную интегральную) матрицу, которая, с другой стороны, по определению является импульсной переходной матрицей:

. (1.20)

Непосредственно из определения вытекают следующие свойства импульсной переходной матрицы:

1. .

2. при всех .

3. . Действительно,

.

Заметим, что импульсная переходная матрица – это такая фундаментальная матрица, которая удовлетворяет начальному условию .

Пример 1.3.

Рассмотрим уравнение простого осциллятора

.

Обозначая и , получим нормальную форму уравнения движения системы в матричном виде:

,

где , , .

Импульсная переходная матрица для этой системы удовлетворяет уравнению

при начальном условии .

Ряд (1.19) для вычисления в этом примере легко суммируется потому, что матрица – постоянная и, кроме того, для нечетных и для четных. Например,

,

,

и т.д.

Простое вычисление показывает, что

,

где использованы разложения тригонометрических функций в ряд Тейлора

Следовательно,

,

.

Пример 1.4.

Рассмотрим неоднородное дифференциальное уравнение

,

которое можно представить в виде нормальной системы уравнений

.

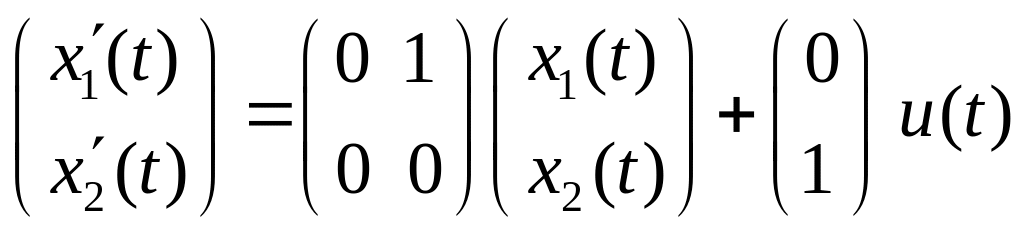Вычисление переходной матрицы немедленно дает

.

Используя формулу Коши

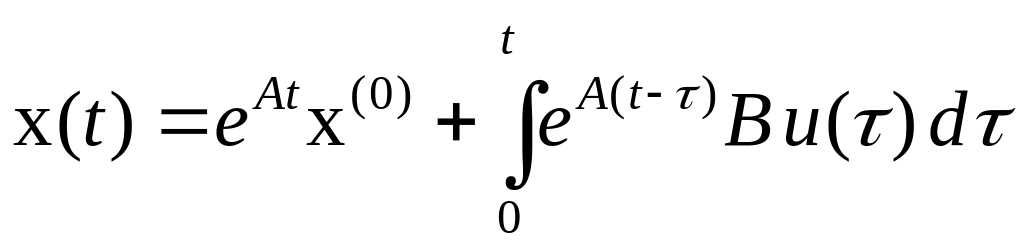
получим общее решение системы

.

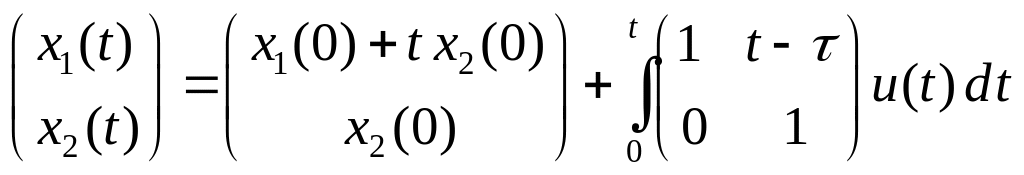Заметим, что несмотря на внешнюю простоту выражения для переходной матрицы в стационарной системе, вычисление функции может оказаться сложной задачей.

С помощью импульсной переходной матрицы можно записать удобную связь между выходными и входными сигналами системы управления (1.13) при условии, что последняя находится в покое до момента подачи входного сигнала. Эта связь устанавливается в соответствии с результатом теоремы 1.3 и имеет вид

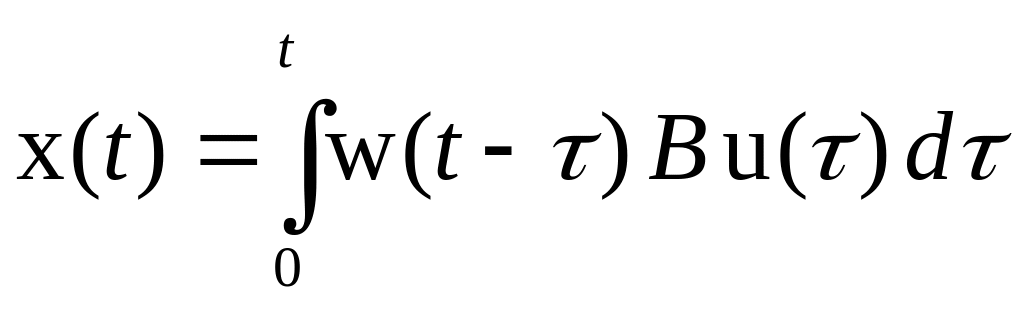. (1.22)

Определение. Пусть импульсная переходная матрица некоторой системы управления. Если существует преобразование Лапласа матрицы , то это преобразование называется передаточной матрицей системы и обозначается через , т. е.

, (1.23)

или, что то же самое,

. (1.24)

Здесь преобразование по Лапласу матрицы понимается как матрица преобразований по Лапласу всех ее элементов.

Применяя преобразование Лапласа к равенству (1.20) и учитывая теорему о свертке (произведение изображений)

,

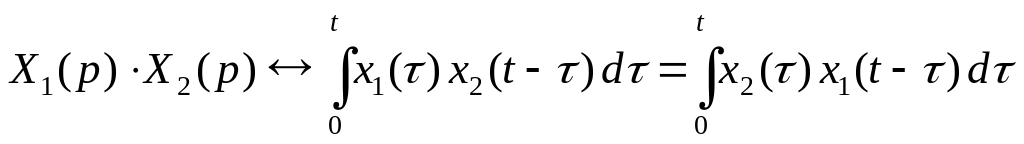для (1.22) можем получить соотношение

,

где

.

Для решения обыкновенных дифференциальных уравнений широко используется аппарат преобразования Лапласа. Этот аппарат можно непосредственно использовать для вычисления импульсной переходной матрицы следующим образом. Используем принятое обозначение для преобразования Лапласа функции : . Тогда, согласно теории этого преобразования, если функция дифференцируема, то

,

где .

Рассмотрим стационарную однородную систему

и ее преобразование Лапласа

.

Тогда

или .

Матрица является характеристической матрицей матрицы , которая является неособенной при всех где – характеристические числа матрицы . Значит, выражение имеет смысл при всех . Взяв обратное преобразование Лапласа, найдем

.

Последовательность вычислений такова:

1. Вычисление обратной матрицы .

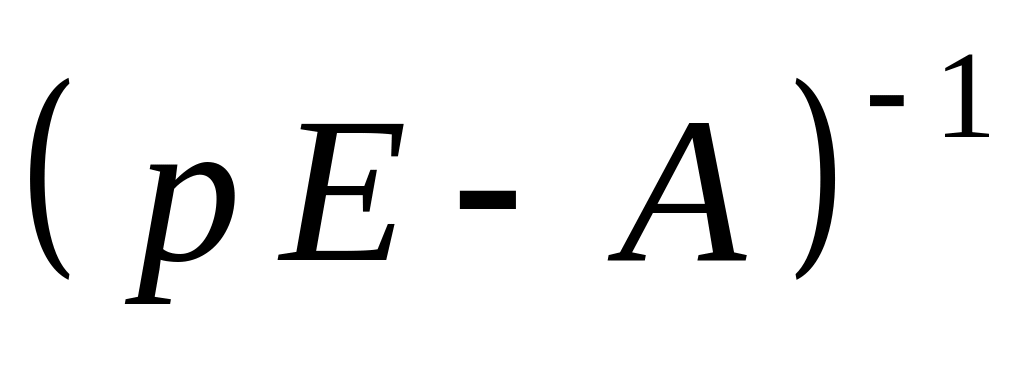2. С помощью таблиц обратного преобразования Лапласа (см. Приложение) определение элементов переходной матрицы

.

Пример 1.5.

Пусть система имеет матрицу . Построить импульсную переходную матрицу.

Характеристическая матрица: .

Вычисляем обратную матрицу. При этом определитель исходной матрицы: . После несложных преобразований обратная матрица будет иметь следующий вид:

.

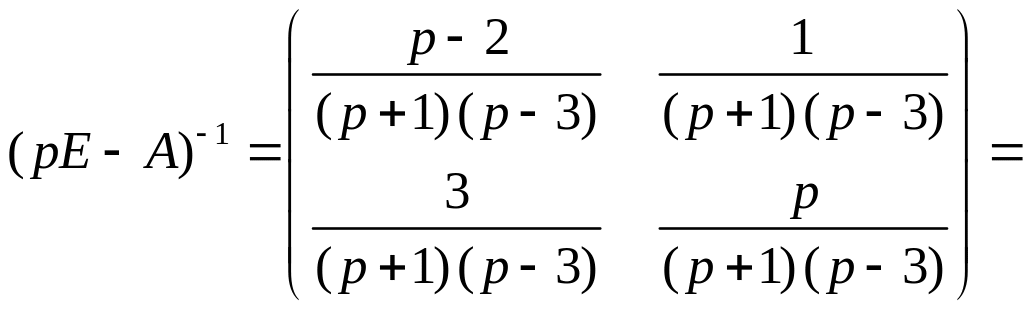
Пользуясь таблицей обратного преобразования Лапласа (см. Приложение), получим

.
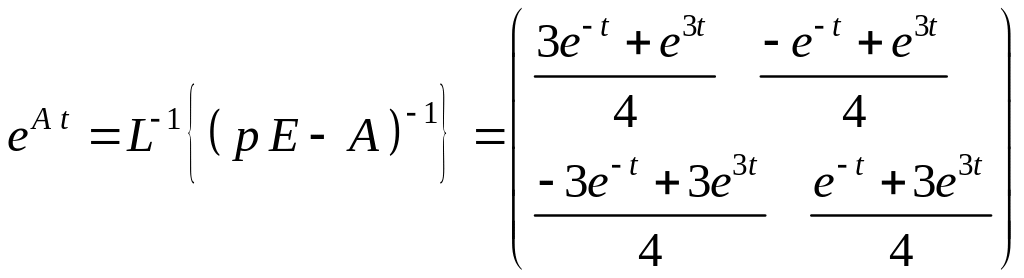