Образец выполнения контрольной работы

Задача 1. Построение импульсной переходной матрицы системы.

Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:

Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа.

Решение.

Исходная система уравнений может быть представлена в матричной форме:

, (1)

где .

Из теории преобразования Лапласа известно, что если дифференцируема, то

,

где .

Тогда преобразование Лапласа системы ( .1) имеет вид

,

или после элементарных преобразований

.

Матрица называется характеристической матрицей матрицы , которая является неособенной при всех , где – характеристические числа матрицы . Следовательно, выражение

имеет смысл при всех .

Взяв обратное преобразование Лапласа, найдем

.

Для матрицы системы (1) последовательно выполняем следующие преобразования:

,

.

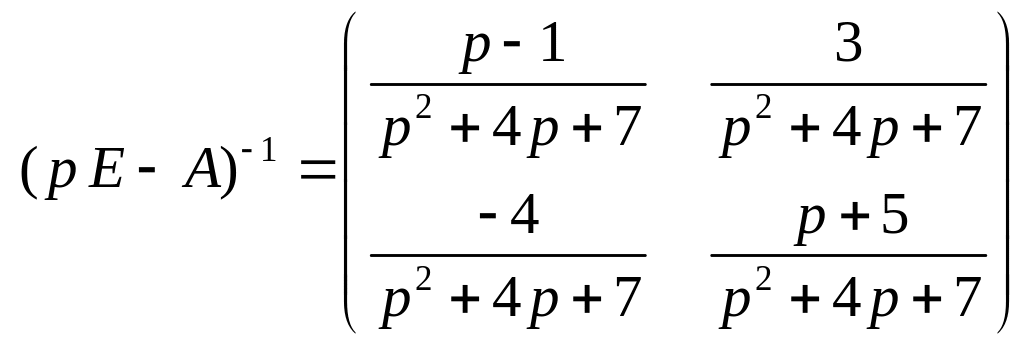Корни характеристического уравнения комплексные , поэтому, выполнив следующие эквивалентные преобразования

,

и обозначив и , можем воспользоваться таблицей 1.1 преобразований Лапласа для затухающей синусоиды и затухающей косинусоиды:

;

;

;

.

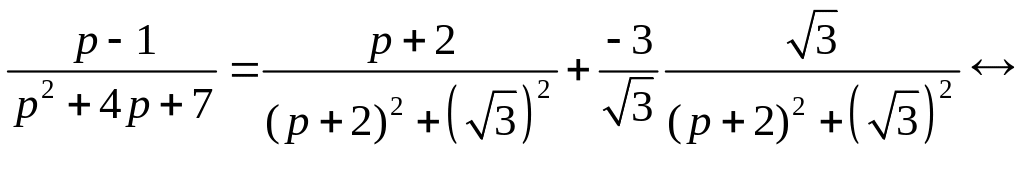
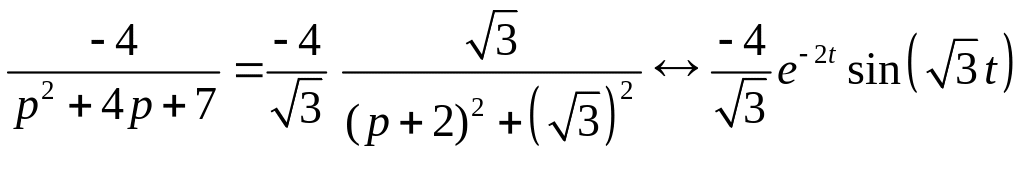Таким образом, импульсная переходная матрица при будет иметь следующий вид:

.

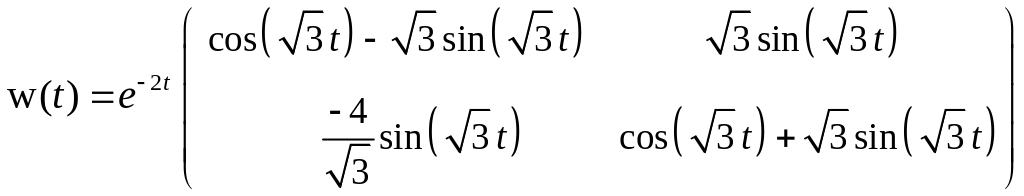Зная импульсную переходную матрицу можно построить решение исходной системы

.

Задача 2. Управляемость и наблюдаемость системы.

Линейная система управления описывается следующей нормальной системой дифференциальных уравнений:

где ; ; .

Исследовать управляемость и наблюдаемость системы. Если система управляема, то построить одно из многих управлений, переводящих систему из состояния в состояние .

Решение.

Из теории известно, что для управляемости -мерной динамической стационарной системой необходимо и достаточно, чтобы ранг матрицы управляемости равнялся . Построим матрицу управляемости исходной системы .

Вычислим следующее произведение:

; .

Таким образом,

и система управляема.

Матрица наблюдаемости для нашей системы вычисляется аналогично. Для того, чтобы -мерная динамическая стационарная система была наблюдаемой, необходимо и достаточно равенство ранга матрицы наблюдаемости . Построим матрицу наблюдаемости исходной системы:

.

Видим, что . Следовательно, система наблюдаема, т.е. по выходным координатам можно восстановить все фазовые координаты системы.

Известно, что если система управляема, то матрица–грамиан управляемости имеет полный ранг, т.е. равный , при любом и для стационарной системы определяется по следующей формуле:

.

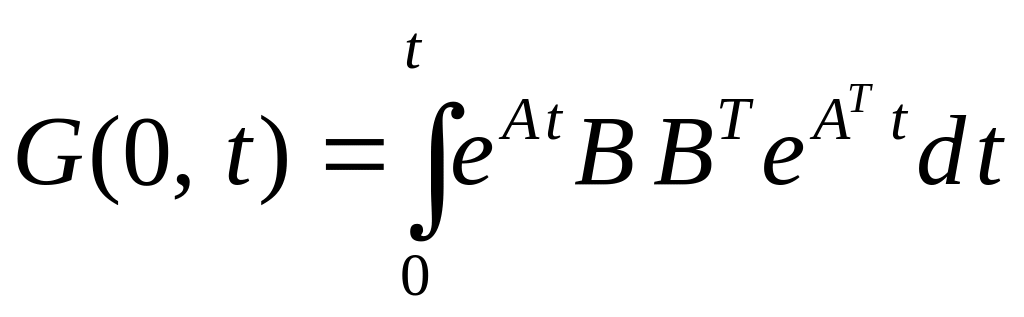Одно из многих управлений, переводящих систему из состояния в состояние можно определить по формуле

, (2)

где – импульсная переходная матрица исходной системы;

– матрица, обратная грамиану управляемости.

Вычисляем импульсную переходную матрицу. Используя обратное преобразование Лапласа:

=

.

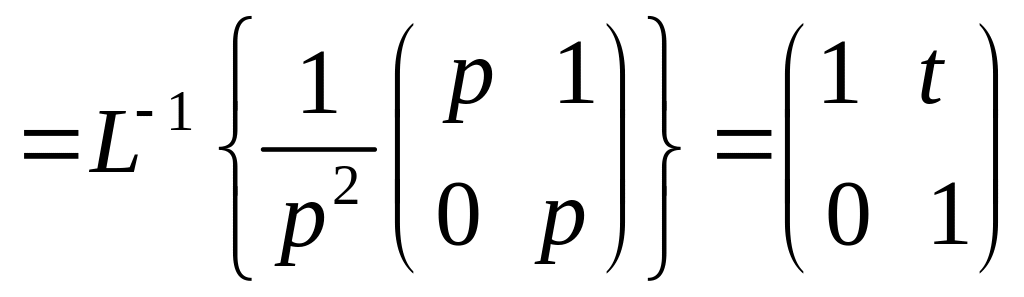Вычисляем грамиан управляемости:

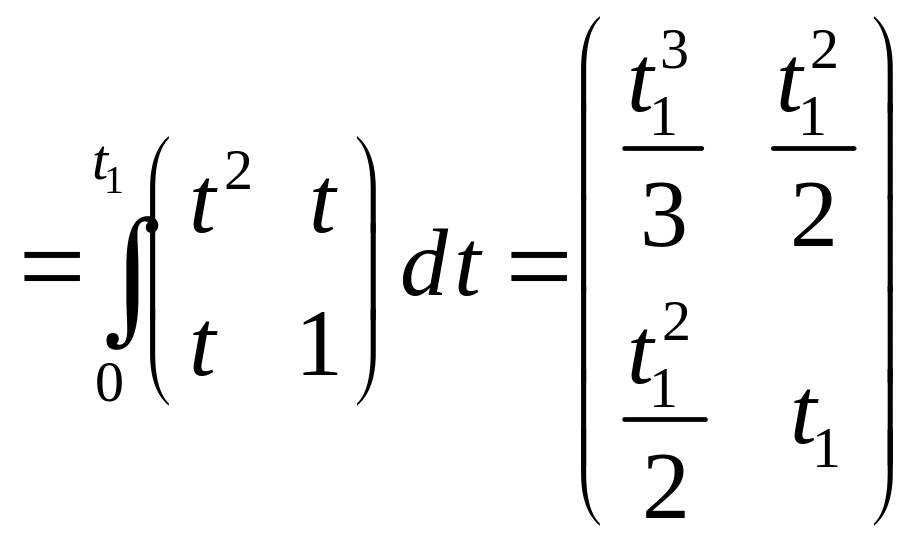. Определитель .

.

Подставляя в формулу (2) импульсную переходную матрицу и матрицу , находим одно из управлений исходной системы при заданных начальных и конечных условиях:

или .

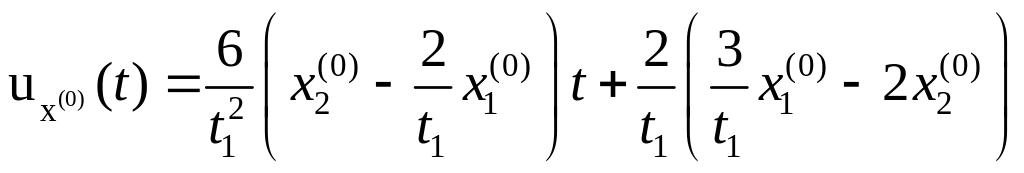Задача 3. Построение оптимального управления методами классического вариационного исчисления.

Линейная система управления описывается следующим дифференциальным уравнением:

,

где ; .

Требуется определить оптимальный процесс перевода системы из одной точки фазового пространства

в другую заданную точку фазового пространства

за фиксированный отрезок времени , затрачивая при этом минимум энергии

управляющего сигнала .

Решение.

Для решения задачи построим вспомогательный функционал с помощью функции Лагранжа

,

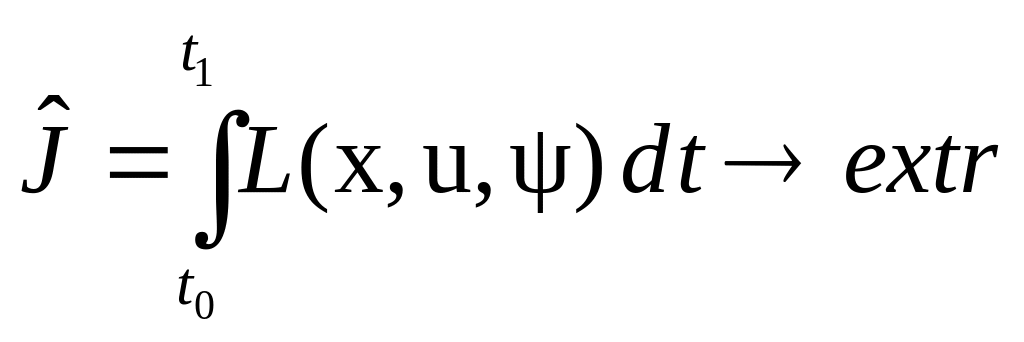где – функция Лагранжа.

В нашем случае функция Лагранжа имеет вид:

.

Для определения параметров оптимального решения используем следующие уравнения Эйлера:

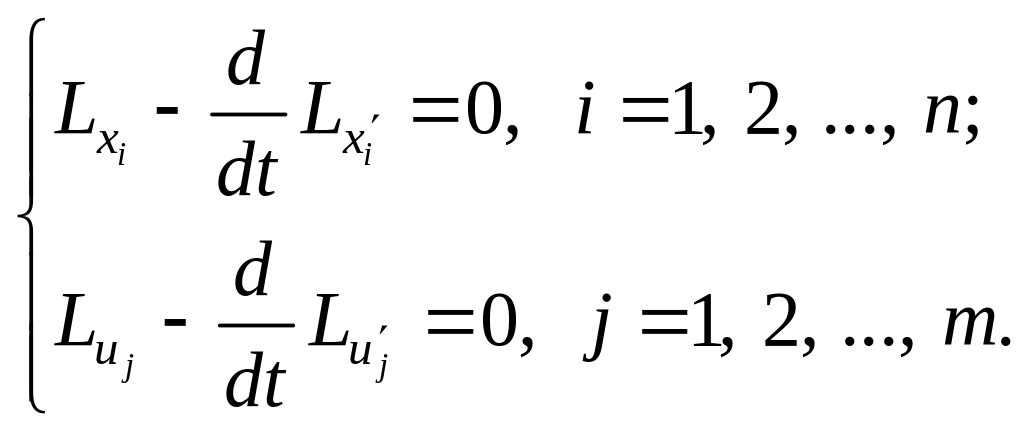
Вычислим все величины системы уравнений Эйлера для нашей задачи

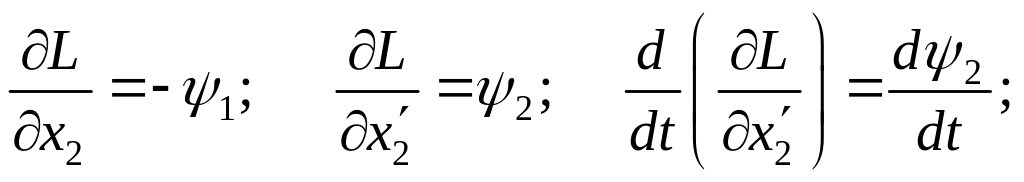
Подставляя найденные величины в уравнения Эйлера, получим систему дифференциальных уравнений:

Отсюда находим

С учетом функции управления исходная система уравнений связи принимает вид

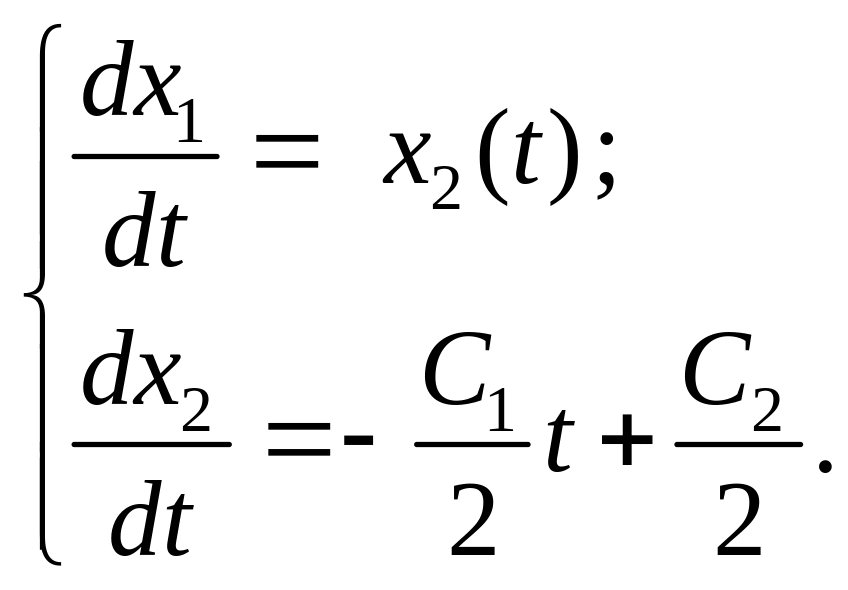
Решая последнюю систему уравнений определяем оптимальное решение для фазовых координат:

Пусть, например, заданы следующие начальные и конечные условия:

Используя краевые условия, получим конкретные значения произвольных постоянных:

Поэтому оптимальное управление и фазовые координаты имеют следующий вид:

Задача 4. Принцип максимума Понтрягина.

Система управления описывается следующим дифференциальным уравнением:

, (1)

где ; .

Требуется определить управление , обеспечивающее быстрейший перевод системы из состояния в начало координат при условии, что на управление должно удовлетворять ограничению .

Решение.

Данная задача о максимальном быстродействии, поэтому функционалом является время процесса управления

.

Таким образом, полная исходная система уравнений объекта будет иметь следующий вид:

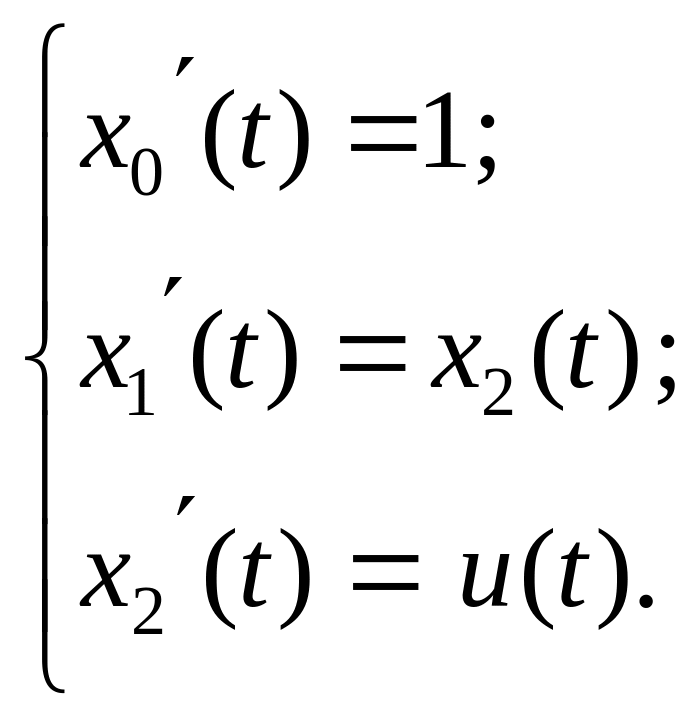
Составляем функцию Гамильтона (4.3)

.

Из последнего выражения видно, что достигнет максимального значения, если

.

Для вспомогательных функций и составим систему сопряженных уравнений (4.5)

решая которую, найдем , . Следовательно, оптимальное управление имеет вид

,

т.е. управление не более чем один раз меняет знак.

Поскольку линейная функция на любом промежутке меняет знак не более одного раза, то какова бы ни была начальная точка , соответствующее оптимальное управление является кусочно-постоянной функцией, принимающей значение + 1 или –1 и имеющей не более двух интервалов постоянства.

Для отрезка времени, на котором из системы (1) ходим уравнение

,

после интегрирования которого получим семейство кривых

.

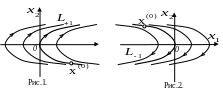
По этим кривым происходит движение изображающей точки системы при . На рис.1 эти траектории изображены с указанием направления движения (из второго уравнения системы (1) видно, что с возрастанием координата возрастает, поэтому движение изображающей точки происходит снизу вверх).

Интегрируя систему уравнений (1) при по аналогии с предыдущим, получим семейство траекторий (рис.2)

.

В каждом из семейств траекторий имеется лишь одна полудуга параболы, по которой изображающая точка может приблизиться к началу координат. На рисунках эти дуги обозначены через и (индексы равны значениям управлений, при которых происходит указанное движение).

Е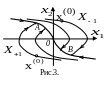 сли изображающая точка в начальный момент времени лежит на дуге , то оптимальное управление , приводящее систему из точки в начало координат за минимальное время, равно , а траектория системы совпадает с некоторым куском линии (рис.1). Если точка лежит на дуге , то , а траектория системы расположена на (рис.2). Только в этих двух случаях оптимальное управление постоянно (в смысле знака) в течение всего времени движения. Во всех других случаях расположения начальной точки на плоскости оптимальное управление меняет свое значение либо с на , либо с на . Оптимальные траектории в этих случаях также состоят из двух частей – одна часть совпадает с куском параболы семейства (если вначале ) или (если вначале ), по которому движение происходит до момента пересечения ee c линией или , а другая часть совпадает с куском линии или от упомянутой точки пересечения до начала координат. На рис.3 изображено все семейство фазовых траекторий рассматриваемой системы.

Как видим, фазовая плоскость разделяется линиями и на две части: и . Если точка ( ), то фазовая точка должна двигаться под воздействием оптимального управления ( ) до точки , после чего ее движение происходит по линии под воздействием управления ( ). Отсюда видно, что на линии происходит переключение знака управления. Благодаря такому свойству, эту линию называют линией переключения.