Вариант 5

Задача 1. Построение импульсной переходной матрицы системы.

Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:

Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа.

Задача 2. Управляемость и наблюдаемость системы.

Линейная система управления описывается следующей нормальной системой дифференциальных уравнений:

где ; ; .

Исследовать управляемость и наблюдаемость системы. Если система управляема, то построить одно из многих управлений, переводящих систему из состояния в состояние .

Задача 3. Построение оптимального управления методами классического вариационного исчисления.

Линейная система управления описывается следующим дифференциальным уравнением:

где ; .

Требуется определить оптимальный процесс перевода системы из одной точки фазового пространства

в другую заданную точку фазового пространства

за фиксированный отрезок времени , затрачивая при этом минимум энергии

управляющего сигнала .

Задача 4. Принцип максимума Понтрягина.

Система управления описывается следующим дифференциальным уравнением:

, (1)

где ; .

Требуется определить управление , обеспечивающее быстрейший перевод системы (1) из состояния в начало координат при условии, что на управление должно удовлетворять ограничению .

Построить фазовые траектории системы управления.

Вариант 6

Задача 1. Построение импульсной переходной матрицы системы.

Линейная динамическая система описывается следующей нормальной системой дифференциальных уравнений:

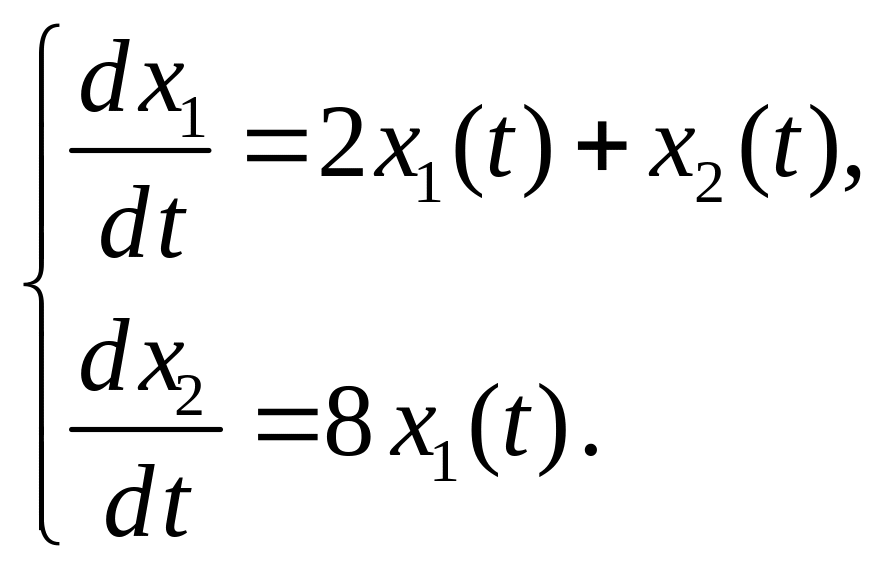
Построить импульсную переходную матрицу системы с помощью обратного преобразования Лапласа.

Задача 2. Управляемость и наблюдаемость системы.

Линейная система управления описывается следующей нормальной системой дифференциальных уравнений:

где ; ; .

Исследовать управляемость и наблюдаемость системы. Если система управляема, то построить одно из многих управлений, переводящих систему из состояния в состояние .

Задача 3. Построение оптимального управления методами классического вариационного исчисления.

Линейная система управления описывается следующим дифференциальным уравнением:

где ; .

Требуется определить оптимальный процесс перевода системы из одной точки фазового пространства

в другую заданную точку фазового пространства

за фиксированный отрезок времени , затрачивая при этом минимум энергии

управляющего сигнала .

Задача 4. Принцип максимума Понтрягина.

Система управления описывается следующим дифференциальным уравнением:

, (1)

где ; .

Требуется определить управление , обеспечивающее быстрейший перевод системы (1) из состояния в начало координат при условии, что на управление должно удовлетворять ограничению .

Построить фазовые траектории системы управления.