83. Формула расчета абсолютного прироста:

где  _i - абсолютный прирост;

y_i- уровень сравниваемого периода;

y₀ - уровень базисного периода.

Формула расчета абсолютного прироста при сравнении с переменной базой:

где   - уровень предшествующего периода.

Если уровень уменьшился по сравнению с базисным, то  <0. В этом случае абсолютный прирост характеризует абсолютное уменьшение (сокращение) уровня.

Между цепными и базисными абсолютными приростами существует определенная взаимосвязь. Так, сумма цепных абсолютных приростов равна соответствующему базисному абсолютному приросту,

84. Коэффициент роста (темп роста) - это отношение двух сравниваемых уровней, которое показывает, во сколько раз данный уровень превышает уровень базисного периода. Отражает интенсивность изменения уровней ряда динамики и показывает, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения - какую часть базисного уровня составляет сравниваемый уровень.

Формула расчета коэффициента роста: при сравнении с постоянной базой: K_i.=y_i /y₀, при сравнении с переменной базой:K_i.=y_i /y_i-1.

Цепные и базисные коэффициенты роста, характеризующие интенсивность изменения производства электроэнергии в Рос­сии по годам и за весь период, исчислены.

Между цепными и базисными коэффициентами роста суще­ствует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведе­ние последовательных цепных коэффициентов роста равно базис­ному коэффициенту роста за весь период ( ), а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

85. Коэффициентом прироста называется отношение абсолютного прироста к уровню, принятому за базу сравнения.

Коэффициенты (темпы) прироста определяют по отношению к непосред­ственно предшествующему уровню ряда динамики (цепные)

iпр. y = (уi - уi-1 )/ уi-1 ,

и по отношению к начальному уровню (базисные)

iпр. y = (уi - у1 )/ у1 .

Коэффициенты роста и коэффициенты прироста связаны между собой, что видно из формул их расчета. Так, цепной коэффициент прироста равен цеп­ному коэффициенту роста минус единица:

86. ?

Абсолютное значение (содержание) 1% (одного процента) прироста - результат деления абсолютного прироста на соответствующий темп прироста:

Эта величина показывает, сколько в абсолютном выражении дает каждый процент прироста.

Все относительные показатели динамики характеризуют интенсивность процесса роста (снижения) уровня.

Средний уровень ряда характеризует обобщённую вели­чину абсолютных уровней. Он рассчитывается по средней хро­нологической, т. е. по средней исчисленной из значений, изме­няющихся во времени.

Методы расчета среднего уровня интервального и моментного рядов динамики различны.

Для интервальных рядов динамики из абсолютных уровней средний уровень за период времени определяется по формуле средней арифметической:

• при равных интервалах применяется средняя арифметиче­ская простая:

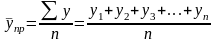; (7.7)

где y – абсолютные уровни ряда, n – число уровней ряда.

• при неравных интервалах- средняя арифметическая взвешенная

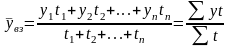; (7.8)

где y₁,…,y_n – уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t₁,…,t_n – веса, длительность интервалов времени (дней, месяцев) между смежными датами.

Средний уровень производства электроэнергии за 1993— 1998 гг. находим по формуле (7.6), так как исследуемый ряд динамики представляет собой интервальный ряд с одинаковыми интервалами, млрд. кВт. ч:

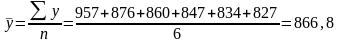
Расчет среднего уровня для интервального ряда динамики с неравностоящими уровнями рассмотрим на примере.

Средний уровень моментного ряда динамики с равностоящими уровнями определяется по формуле средней хронологической мо­ментного ряда:

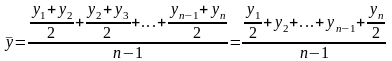; (7.9)

где y₁…y_n - уровни периода, за который делается расчет;

п - число уровней;

п - 1 - длительность периода времени.

Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний абсолютный при­рост как среднюю арифметическую простую:

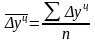(7.11)

где п - число цепных абсолютных приростов 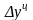в изучаемом периоде.

Средний абсолютный прирост определим через накопленный (базисный) абсолютный прирост (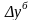 ). Для случая равных ин­тервалов применим следующую формулу:

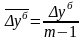(7.12)

где т — число уровней ряда динамики в изучаемом периоде, включая базисный.

90. Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий, во сколько раз в среднем за едини­цу времени изменяется уровень ряда динамики.

Средний темп роста (снижения) — обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа роста (сни­жения) применяется определяющий показатель — произведение цепных темпов роста, равное темпу роста за весь рассматривае­мый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то согласно общему пра­вилу (см. гл.5.1.) нужно применять среднюю геометрическую.

Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (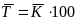 ), то для равностоящих рядов динамики расчеты по средней геомет­рической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по «цепному способу»):

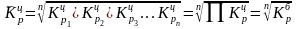, (7.13)

где п - число цепных коэффициентов роста;

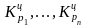- цепные коэффициенты роста; 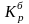- базисный ко­эффициент роста за весь период.

В нашем примере среднегодовой темп изменения производ­ства электроэнергии с 1994 по 1998 гг.:

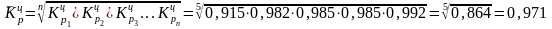
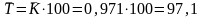т.е. 97,1%

Следовательно, с 1994 по 1999 гг. производство электро­энергии в России снижалось в среднем на 2,9% в год, т. е. (0,971 * 100 - 100).

Если известны уровни динамического ряда, то расчет сред­него коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкорен­ное выражение подставляется базисный коэффициент роста. Ба­зисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода у„ на уровень базисного периода у₀.

Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу»):

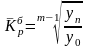, (7.14)

где т — число уровней ряда динамики в изучаемом периоде, вклю­чая базисный.

Для расчета средних коэффициентов роста по формуле (7.14) не нужно знать годовые темпы. Для нашего примера:

.

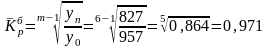Получен тот же результат, расчеты упрощены.

91. Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100 %. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:

; ,

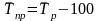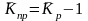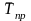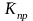где — средний темп прироста, — средний коэффициент прироста

Если уровни ряда динамики снижаются, то средний темп роста будет меньше 100%, а средний темп прироста — отрица­тельной величиной. Отрицательный темп прироста 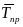пред­ставляет собой средний темп сокращения и характеризует сред­нюю относительную скорость снижения уровня.

Так, в нашем примере среднегодовой темп прироста произ­водства электроэнергии характеризуется отрицательным значе­нием (-2,9%), что свидетельствует о ежегодном сокращении производства электроэнергии.

При анализе развития явлений, отражаемых двумя динамиче­скими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамиче­ских рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к раз­личным организациям (министерствам, предприятиям, учрежде­ниям), или при сравнении рядов разного содержания, но харак­теризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах.

Сравнительные характеристики направления и интенсивно­сти роста одновременно развивающихся во времени явлений определяются приведением рядов динамики к общему (единому) основанию и расчетом коэффициентов опережения (отставания).

Ряды динамики (в которых возникают, например, про­блемы сопоставимости цен сравниваемых стран, методики рас­чета сравниваемых показателей и т.п.) обычно приводят к одно­му основанию, если они не могут быть решены другими метода­ми. По исходным уровням нескольких рядов динамики опреде­ляют относительные величины - базисные темпы роста или прироста. Принятый при этом за базу сравнения период време­ни (дата) выступает в качестве постоянной базы расчетов тем­пов роста для каждого из изучаемых рядов динамики. В зависи­мости от целей исследования базой может быть начальный, средний или другой уровень ряда.

92. Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.

Задача состоит в том, чтобы выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различ­ных случайных факторов. С этой целью ряды динамики подвергаются обработке методами укрупнения ин­тервалов, скользящей средней и аналитического выравнивания.

Одним из наиболее простых методов изучения основной тенденции в рядах динамики является укрупнение интервалов. Он основан на укрупнении периодов времени, к которым отно­сятся уровни ряда динамики (одновременно уменьшается коли­чество интервалов). Например, ряд ежесуточного выпуска про­дукции заменяется рядом месячного выпуска продукции и т.д. Средняя, исчисленная по укрупненным интервалам, позволяет выявлять направление и характер (ускорение или замедление роста) основной тенденции развития.

Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из опреде­ленного числа, обычно нечетного (3, 5, 7 и т.д.), первых по сче­ту уровней ряда, затем - из такого же числа уровней, но начи­ная со второго по счету, далее — начиная с третьего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, пере­двигаясь на один срок.

Сглаженный ряд урожайности по трехлетиям короче факти­ческого на один член ряда в начале и в конце, по пятилетиям - на два члена в начале и конце ряда. Он меньше, чем фактиче­ский подвержен колебаниям из-за случайных причин, и четче, в виде некоторой плавной линии на графике (рис. 7.4), выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития.

Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следователь­но, потеря информации.

Для того чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во вре­мени, используется аналитическое выравнивание ряда динамики.

Основным содержанием метода аналитического выравнива­ния в рядах динамики является то, что общая тенденция разви­тия рассчитывается как функция времени:

,

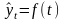где 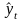— уровни динамического ряда, вычисленные по соответст­вующему аналитическому уравнению на момент времени t.

96. где — уровни динамического ряда, вычисленные по соответст­вующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней произ­водится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимиру­ет) основную тенденцию ряда динамики.

Выбор типа модели зависит от цели исследования и должен быть основан на теоретическом анализе, выявляющем характер развития явления, а также на графическом изображении ряда динамики (линейной диаграмме).

Например, простейшими моделями (формулами), выражаю­щими тенденцию развития, являются:

линейная функция – прямая = а₀+ a₁t

где а₀, a₁ – параметры уравнения; t – время;

показательная функция = а₀a₁^t ;

степенная функция – кривая второго порядка (парабола)

=а₀+ a₁t + a₂t² .

В тех случаях, когда требуется особо точное изучение тен­денции развития (например, модели тренда для прогнозирова­ния), при выборе вида адекватной функции можно использовать специальные критерии математической статистики.

Параметры уравнения а_i, удовлетворяющие этому условию, могут быть найдены решением системы нормальных уравнений. На основе найденного уравнения тренда вычисляются выровненные уровни. Таким образом, выравнивание ряда динамики заключается в замене фактических уровней у_i плавно изменяю­щимися уровнями , наилучшим образом аппроксимирующи­ми статистические данные.

• Выравнивание по прямой используется, как правило, в тех случаях, когда абсолютные приросты практически посто­янны, т. е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

Рассмотрим «технику» выравнивания ряда динамики по пря­мой: = а₀+ a₁t. Параметры а₀, a₁ согласно методу наимень­ших квадратов находятся решением следующей системы нор­мальных уравнений, полученной путем алгебраического преобра­зования условия (7.17):

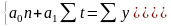_(7.18)

где у — фактические (эмпирические) уровни ряда; t — время (по­рядковый номер периода или момента времени).

Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент).

В статистике периодические колебания, которые имеют опре­деленный и постоянный период, равный годовому промежутку, носят название «сезонные колебания» или «сезонные волны», а дина­мический ряд в этом случае называют сезонным рядом динамики.

Сезонные колебания наблюдаются в различных отраслях экономики: при производстве большинства сельскохозяйствен­ных продуктов, их переработке, в строительстве, транспорте, торговле и т.д. Значительной колеблемости во внутригодовой динамике подвержены денежное обращение и товарооборот. Наибольшие денежные доходы образуются у населения в III и IV кварталах, особенно это характерно для селян. Максималь­ный объем розничного товарооборота приходится на конец ка­ждого года. Спрос на многие виды услуг, производство молока, яиц, мяса, шерсти, улов рыбы колеблется по сезонам.

Сезонные колебания обычно отрицательно влияют на ре­зультаты производственной деятельности, вызывая нарушения ритмичности производства. Поэтому хозяйственные организа­ции принимают меры для смягчения сезонности за счет рацио­нального сочетания отраслей, механизации трудоемких процес­сов, создания агропромышленных фирм и т.д.

Комплексное регулирование сезонных изменений по отдель­ным отраслям экономики должно основываться на исследова­нии сезонных колебаний.

В статистике существует ряд методов изучения и измерения се­зонных колебаний. Самый простой заключается в построении специ­альных показателей, которые называются индексами сезонности I_s. Совокупность этих показателей отражает сезонную волну.

Индексами сезонности являются процентные отношения факти­ческих (эмпирических) внутригрупповых уровней к теоретическим (расчетным) уровням, выступающим в качестве базы сравнения.

Для того чтобы выявить устойчивую сезонную волну, на ко­торой не отражались бы случайные условия одного года, индек­сы сезонности вычисляют по данным за несколько лет (не менее трех), распределенным по месяцам.

Если ряд динамики не содержит ярко выраженной тенден­ции в развитии, то индексы сезонности вычисляются непосред­ственно по эмпирическим данным без их предварительного вы­равнивания.

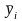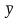Для каждого месяца рассчитывается средняя величина уровня, например за три года ( ), затем вычисляется среднемесяч­ный уровень для всего ряда . После чего определяется показатель сезонной волны — индекс сезонности I_s как процентное от­ношение средних для каждого месяца к общему среднемесячно­му уровню ряда, %

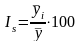, (7.22)

где - средний уровень для каждого месяца (минимум за три года);

- среднемесячный уровень для всего ряда.

Под экстраполяцией понимают нахождение уровней за пре­делами изучаемого ряда, т. е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). Поскольку в действительности тенденция развития не остается неизмен­енной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки.

Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней и подставляя в него значения t за пределами исследованного ряда, рассчитывают для t вероятностные .

В соответствии с жестко детерминистическим представлением о функционировании экономических систем необходимость и закономерность однозначно проявляются в каждом отдельном явлении, т. е. любое действие вызывает строго определенный ре­зультат; случайными (непредвиденными заранее) воздействиями при этом пренебрегают. Поэтому при заданных начальных усло­виях состояние такой системы может быть определено с вероят­ностью, равной единице. Разновидностью такой закономерности является функциональная связь.

Связь признака у с признаком x называется функциональ­ной, если каждому возможному значению независимого призна­ка х соответствует одно или несколько строго определенных значений зависимого признака у. Определение функциональ­ной связи может быть легко обобщено для случая многих при­знаков х₁, х_2,...,х_п.

Характерной особенностью функциональных связей является то, что в каждом отдельном случае известен полный перечень факторов, определяющих значение зависимого (результативно­го) признака, а также точный механизм их влияния, выражен­ный определенным уравнением.

Функциональную связь можно представить уравнением:

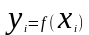
где y_i — результативный признак (i = 1,...,n);

f(Xi) — известная функция связи результативного и факторного при­знаков;

x_i— факторный признак

Стохастическая связь — это связь между величинами, при которой одна из них, случайная величина у, реагирует на изменение другой величины х или других величин х₁, х_2,...,х_п (случайных или неслучайных) изменением закона распределения. Это обусловливается тем, что зависимая переменная (результативный признак), кроме рассматриваемых независимых, подвержена влиянию ряда неучтенных или неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибок измерения переменных. Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.

Характерной особенностью стохастических связей является то, что они проявляются во всей совокупности, а не в каждой ее единице (причем не известен ни полный перечень факторов, определяющих значение результативного признака, ни точный механизм их функционирования и взаимодействия с результативным признаком). Всегда имеет место влияние случайного. Появляющиеся различные значения зависимой переменной — реализации случайной величины.

Модель стохастической связи может быть представлена в общем виде уравнением:

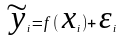(9.1)

где 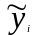— расчетное значение результативного признака;

f(x_i ) — часть результативного признака, сформировавшаяся под воз-

действием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком;

ε_i— часть результативного признака, возникшая вследствие

действия неконтролируемых или неучтенных факторов, а также измерения признаков, неизбежно сопровождающегося некоторыми случайными ошибками.

Корреляционная связь существует там, где взаимосвязанные явления характеризуются только случайными величинами. При такой связи среднее значение (математическое ожидание) случайной величины результативного признака у закономерно изменяется в зависимости от изменения другой величины x или других случайных величин х₁, х_2,...,х_п. Корреляционная связь проявляется не в каждом отдельном случае, а во всей совокупности в целом. Только при достаточно большом количестве случаев каждому значению случайного признака х будет соответствовать распределение средних значений случайного признака y. Наличие корреляционных связей присуще многим общественным явлениям.

Прямые и обратные связи. В зависимости от направления действия функциональные и стохастические связи могут быть прямыми и обратными. При прямой связи направление измене­ния результативного признака совпадает с направлением изме­нения признака-фактора, т. е. с увеличением факторного при­знака увеличивается и результативный, и наоборот, с уменьше­нием факторного признака уменьшается и результативный при­знак. В противном случае между рассматриваемыми величинами существуют обратные связи. Например, чем выше квалифика­ция рабочего (разряд), тем выше уровень производительности труда — прямая связь. А чем выше производительность труда, тем ниже себестоимость единицы продукции — обратная связь.

Прямолинейные и криволинейные связи. По аналитическо­му выражению (форме) связи могут быть прямолинейными и криволинейными. При прямолинейной связи с возрастанием значения факторного признака происходит непрерывное возрас­тание (или убывание) значений результативного признака. Математически такая связь представляется уравнением прямой, а графически — прямой линией. Отсюда ее более короткое название — линейная связь.

При криволинейных связях с возрастанием значения фак­торного признака возрастание (или убывание) результатив­ного признака происходит неравномерно или же направление его изменения меняется на обратное. Геометрически такие связи представляются кривыми линиями (гиперболой, пара­болой и т.д.).

Однофакторные и многофакторные связи. По количеству факторов, действующих на результативный признак, связи раз­личаются однофакторные (один фактор) и многофакторные (два и более факторов). Однофакторные (простые) связи обыч­но называются парными (так как рассматривается пара призна­ков). Например, корреляционная связь между прибылью и производительностью труда. В случае многофакторной (множе­ственной) связи имеют в виду, что все факторы действуют комплексно, т.е. одновременно и во взаимосвязи, например, корреляционная связь между производительностью труда и уровнем организации труда, автоматизации производства, ква­лификации рабочих, производственным стажем, простоями и другими факторными признаками.

С помощью множественной корреляции можно охватить весь комплекс факторных признаков и объективно отразить су­ществующие множественные связи.

В общем виде задача статистики в области изучения взаимо­связей состоит не только в количественной оценке их наличия, направления и силы связи, но и в определении формы (аналитического выражения) влияния факторных признаков на результативный. Для ее решения применяют методы корреляционного и регрессионного анализа.

Задачи корреляционного анализа сводятся к измерению тесноты известной связи между варьирующими признаками, определению неизвестных причинных связей (причинный характер которых, должен быть выяснен с помощью теоретического анализа) и оценке факторов, оказывающих наибольшее влияние на резуль­тативный признак.

Задачи регрессионного анализа — выбор типа модели (формы связи), установление степени влияния независимых перемен­ных на зависимую и определение расчетных значений зависи­мой переменной (функции регрессии).

Решение всех названных задач приводит к необходимости комплексного использования этих методов.

Исследование связей в условиях массового наблюдения и действия случайных факторов осуществляется, как правило, с помощью экономико-статистических моделей. В широком смысле модель — это аналог, условный образ (изображение, описание, схема, чертеж и т.п.) какого-либо объекта, процес­са или события, приближенно воссоздающий «оригинал». Модель представляет собой логическое или математическое описание компонентов и функций, отображающих сущест­венные свойства моделируемого объекта или процесса, дает возможность установить основные закономерности изменения оригинала. В модели оперируют показателями, исчисленными для качественно однородных массовых явлений (совокупно­стей). Выражение модели в виде функциональных уравнений используют для расчета средних значений моделируемого по­казателя по набору заданных величин и для выявления степе­ни влияния на него отдельных факторов.

По количеству включаемых факторов модели могут быть однофакторными и многофакторными (два и более факторов).

В зависимости от познавательной цели стати­стические модели подразделяются на структурные, динамические и модели связи.

Рассмотрим основные проблемы статистического моделирования связи методами корреляционного и регрессионного анализа.

Уравнение однофакторной (парной) линейной корреляционной связи имеет вид:

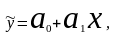(9.2)

де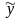 — теоретические значения результативного признака, полу­ченные по уравнению регрессии;

a_0, a₁— коэффициенты (параметры) уравнения регрессии.

Поскольку a₀ является средним значением у в точке х = 0,

экономическая интерпретация часто затруднена или вообще

невозможна.

109. ?

110. ?

111. ?

112. ?

113. ?

114. ?

115. ?

Для удобства интерпретации параметра a₁используют коэф­фициент эластичности. Он показывает средние изменения ре­зультативного признака при изменении факторного признака на 1% и вычисляется по формуле, %:

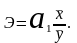
117. Для измерения тесноты связи между двумя из рассматривае­мых переменных (без учета их взаимодействия с другими пере­менными) применяются парные коэффициенты корреляции. Методика расчета таких коэффициентов и их интерпретация аналогичны методике расчета линейного коэффициента корре­ляции в случае однофакторной связи. Если известны средние квадратические отклонения анализируемых величин, то парные коэффициенты корреляции можно рассчитать проще по следующим формулам:

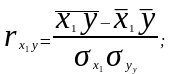(9.16)

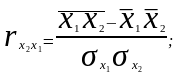
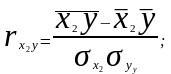(9.17)

Однако в реальных условиях все переменные, как прави­ло, взаимосвязаны. Теснота этой связи определяется частными коэффициентами корреляции, которые характеризуют степень и влияние одного из аргументов на функцию при ус­ловии, что остальные независимые переменные закреплены на постоянном уровне. В зависимости от количества пере­менных, влияние которых исключается, частные коэффици­енты корреляции могут быть различного порядка: при исклю­чении влияния одной переменной получаем частный коэффициент корреляции первого порядка; при исключении влия­ния двух переменных — второго порядка и т.д. Парный коэф­фициент корреляции между функцией и аргументом обычно не равен соответствующему частному коэффициенту.

Частный коэффициент корреляции первого порядка между при­знаками x₁и у при исключении влияния признака x₂ вычисляют по формуле:

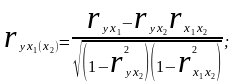(9.19)

то же – зависимость y от x₂ при исключении влияния x_1:

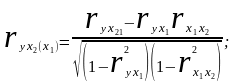(9.20)

Можно рассчитать взаимосвязь факторных признаков при устранении влияния результативного признака: