
- •Ответы на экзамен по статистике.
- •Развитие статистики как науки шло по двум направлениям.
- •Методы статистики
- •Основные правила построения статистических таблиц:
- •Диаграммы принято подразделять по их форме на следующие виды:
- •Виды относительных величин
- •Относительная величина динамики
- •Правило мажорантности средних величин
- •Основные свойства средней арифметической
- •Правило сложения дисперсий:
- •Суммирование уровней моментного ряда динамики не имеет смысла, так как одни и те же единицы совокупности обычно входят в состав нескольких уровней.
- •Формула расчета абсолютного прироста:
- •Совокупный коэффициент множественной
Правило мажорантности средних величин
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина:
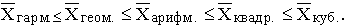
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по не сгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности.
Формула средней арифметической (простой) имеет вид
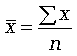
Основные свойства средней арифметической
- Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты.
Другими словами, постоянный множитель может быть вынесен за знак средней
- Если от каждой варианты отнять (прибавить) какое-либо произвольное число, то новая средняя уменьшится (увеличится) на то же число:
- Если каждую варианту умножить (разделить) на какое-то произвольное число, то средняя арифметическая увеличится (уменьшится) во столько раз
- Если все частоты (веса) разделить или умножить на какое-либо число, то средняя арифметическая от этого не изменится. Дело в том, что веса при исчислении средней арифметической выполняют роль удельного веса (соотношений между группами по количеству единиц). Поэтому замена частот частностями не меняет средней.
- Сумма отклонений отдельных вариантов от средней арифметической всегда равняется нулю.
Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1.
Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1:
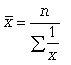
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).
В качестве структурных средних применяют показатели моды и медианы.
Мода и медиана определяются лишь структурой распределения. Поэтому их именуют структурными позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
Мода - типичная величина, в том смысле, что она встречается в совокупности или объективно может встретиться чаще других. Она имеет важное значение для решения некоторых задач, например какой высоты должны быть предназначенные для массового потребления станки, столы и т. п., какое количество детей чаще всего встречается в семье, какое время дня является «пиковым» для работы предприятий общественного питания, электростанций, городского транспорта и др., какой уровень выполнения плана наиболее часто встречается в том или ином коллективе рабочих или предприятий и т. п.
Особенности применения моды:
1) если все значения вариационного ряда имеют одинаковую частоту, то говорят, что этот вариационный ряд не имеет моды;
2) если две соседних варианты имеют одинаковую доминирующую частоту, то мода вычисляется как среднее арифметическое этих вариант;
3) если две несоседних варианты имеют одинаковую доминирующую частоту, то такой вариационный ряд называется бимодальным;
4) если таких вариант более двух, то ряд полимодальный.
Определение модального интервала в случае интервального вариационного ряда:
1) с равными интервалами модальный интервал определяется по наибольшей частоте;
2) при неравных интервалах - по наибольшей плотности.
Формула определения моды при равных интервалах внутри модального интервала:
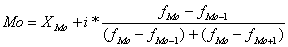
Медиана - это значение изучаемого признака, приходящееся на середину ранжированной совокупности.
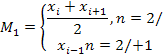
Порядок вычисления медианы:
при вычислении медианы интервального вариационного ряда сначала находят медианный интервал l*u I хы +h\, где Л - длина медианного интервала. Для этого можно использовать кумулятивное распределение частот или относительных частот. Медианному интервалу соответствует тот, в котором содержится накопленная частота, равная 1/2;
|
внутри найденного интервала расчет медианы производится по формуле:
где Wcm , - кумулятивная частота интервала, предшествующего медианному;
Wm- относительная частота медианного интервала.
Применение свойства медианы:
при проектировании оптимального положения остановок общественного транспорта; при проектировании складских помещений; при сооружении бензозаправок и т. д.
Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности (R = Хmax- Xmin). Этот показатель дает самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Зависимость от крайних значений признака придает размаху вариации неустойчивый, случайный характер.
Размах вариации не связан с частотами в вариационном ряду. т. е. с характером распределения. Размах вариации не дает никакой информации об особенностях исследуемых совокупностей и не позволяет оценить степень типичности полученных средних. Область применения этого показа-геля ограничена достаточно однородными совокупностями.
Среднее линейное отклонение представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:
![]()
![]()
где d - среднее линейное отклонение;
|![]() |
- абсолютное значение (модуль) отклонения
варианта от средней арифметической;
|
- абсолютное значение (модуль) отклонения
варианта от средней арифметической;
f-частота.
Первая формула применяется, если каждый из вариантов встречается в совокупности только один раз, а вторая - в рядах с неравными частотами. Необходимость использования в формулах среднего линейного отклонения модулей отклонений вариантов от средней вызвана тем, что алгебраическая сумма этих отклонений равна нулю по свойствам средней арифметической. Среднее линейное отклонение показывает, насколько в среднем колеблется величина признака у единиц исследуемой совокупности, и выражается в тех же единицах измерения, что и варианты.
Дисперсия (
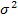 ) - средняя
из квадратов отклонений вариантов
значений признака от их средней величины:
) - средняя
из квадратов отклонений вариантов
значений признака от их средней величины:
![]()
Или ![]() для
не сгруппированных данных,
для
не сгруппированных данных,
![]() для
сгруппированных данных.
для
сгруппированных данных.
Свойства дисперсии.
1. Дисперсия постоянной величины равна 0.
2. Уменьшение всех значений признака на одну и ту же величину не изменяет величину дисперсии:
![]()
3. Уменьшение
всех значений признака в к раз
уменьшает дисперсию в k2 раз: ![]()
4. Средний
квадрат отклонений, исчисленный от
среднего арифметического, всегда будет
меньше среднего квадрата отклонений,
исчисляемого от любой другой
величины: ![]() >
> ![]() . Величина
различия между ними вполне определенная,
это квадрат разности между средней и
этой условной величиной А.
. Величина
различия между ними вполне определенная,
это квадрат разности между средней и
этой условной величиной А.
![]()
![]()
![]()
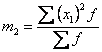 - момент
второго порядка;
- момент
второго порядка;Среднее квадратическое отклонение
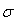 равно
корню квадратному из
дисперсии:
§ для
не сгруппированных данных
равно
корню квадратному из
дисперсии:
§ для
не сгруппированных данных
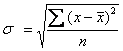
§ для
вариационного ряда
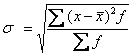 .
Среднее
квадратическое отклонение
— это обобщающая характеристика
размеров вариации признака в совокупности;
оно показывает, на сколько в среднем
отклоняются конкретные варианты от
их среднего значения; является абсолютной
мерой колеблемости признака и выражается
в тех же единицах, что и варианты, поэтому
экономически хорошо интерпретируется.
.
Среднее
квадратическое отклонение
— это обобщающая характеристика
размеров вариации признака в совокупности;
оно показывает, на сколько в среднем
отклоняются конкретные варианты от
их среднего значения; является абсолютной
мерой колеблемости признака и выражается
в тех же единицах, что и варианты, поэтому
экономически хорошо интерпретируется.
Коэффициент вариации используют не только для сравнительной оценки вариации единиц совокупности, но и как характеристику однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33 %.
![]()
Оценка степени интенсивности вариации возможна только для каждого отдельного признака и совокупности определенного состава. При этом при равенстве коэффициентов вариации для различных признаков или в разных совокупностях вариация в одних случаях может считаться как сильная, а в других - как слабая. Различная сила, интенсивность вариации обусловлены объективными причинами.
Общая дисперсия
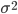 характеризует
вариацию признака во всей совокупности,
сложившуюся под влиянием всех факторов
и условий.
характеризует
вариацию признака во всей совокупности,
сложившуюся под влиянием всех факторов
и условий.Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся по влиянием других, не учитываемых в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий.
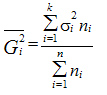
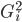 —
дисперсия
i-ой группы.
—
дисперсия
i-ой группы.
Все
три дисперсии (![]() )
связаны между собой следующим равенством,
которое известно как правило
сложения дисперсий:
)
связаны между собой следующим равенством,
которое известно как правило
сложения дисперсий:
![]()
на
этом соотношении строятся показатели,
оценивающие влияние признака группировки
на образование общей вариации. К ним
относятся эмпирический коэффициент
детерминации (![]() )
и эмпирическое корреляционное отношение
(
)
и эмпирическое корреляционное отношение
(![]() )
)
Внутригрупповой дисперсией называется средняя арифметическая дисперсий, где каждое слагаемое входит с весом объема группы.
![]()
Межгрупповая дисперсия
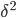 измеряет
систематическую вариацию, обусловленную
влиянием фактора, по которому произведена
группировка:
измеряет
систематическую вариацию, обусловленную
влиянием фактора, по которому произведена
группировка:
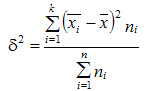
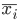 —
групповые
средние,
—
групповые
средние,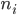 —
численность
единиц i-й
группы
—
численность
единиц i-й
группы
