5.3.2 Виражи на автомобильных дорогах

На кривых, радиусы которых меньше 3000 м для автомобильных дорог 1 категории и 2000 м - для других категорий, устраивают виражи, т. е. дорожному полотну придают односкатный поперечный профиль с наклоном к центру кривой.

Односкатный профиль сохраняется на всем протяжении круговой кривой. Переход от односкатного профиля к нормальному, двухскатному, так называемый отгон виража, делается на переходных кривых или на прямых участках, примыкающих к закруглению.

На кривых малых радиусов вираж имеет дополнительное уширение проезжей части, отвод которого осуществляется также в пределах переходной кривой.

Общая схема виража показана на рисунке 5.26. Основными элементами виража являются:

- уклон виража, т. е. величина односкатного поперечного уклона дорожного полотна;

- длина отгона виража;

- длина виража;

- величина уширения проезжей части.

Рисунок 5.26 — Схема виража автодороги

Поперечный уклон виража зависит от радиуса кривой. При радиусах 3000 – 1000 м уклон виража назначают равным поперечному уклону проезжей части при двухскатном профиле. Для радиусов кривых меньше 1000 м уклон виража проектируют больше поперечного уклона проезжей части. Наибольший уклон виража допускают равным 60 ‰ (R 600 м).

Отгон виража представляет собой плавный переход от двухскатного поперечного профиля к односкатному, при этом главное изменение претерпевает наружная часть дорожного полотна.

Если уклон виража равен поперечному уклону проезжей части, то переход от двухскатного профиля к односкатному осуществляется путем вращения наружной половины полотна около оси дороги. Внутренняя часть полотна остается без изменения.

При уклоне виража, превышающем уклон нормального профиля, на отгоне происходит постепенное вращение всего дорожного полотна около внутренней кромки проезжей части, профильные высоты которой не меняются.

Можно представить, что на отгоне виража поверхность дороги образуется движением поперечных прямых по двум непараллельным направляющим - поднимающейся наружной бровке АА' и оси вращения ВВ' или СС', лежащих в параллельных вертикальных плоскостях (рисунок 5.27). Поперечные прямые, непрерывно меняя свой наклон, все время остаются перпендикулярными к оси. Следовательно, эта поверхность образуется двумя системами прямых - продольных, параллельных вертикальной плоскости, проходящей через ось дороги, и поперечных, расположенных в вертикальных плоскостях, перпендикулярных к оси дороги. Из аналитической геометрии известно, что такой особенностью обладают образующие линейчатой косой поверхности - гиперболического параболоида.

В пределах круговой кривой односкатное дорожное полотно представляет собой коническую поверхность.

При отгоне виража наружная бровка полотна возводится с некоторым дополнительным продольным уклоном i₂, чтобы в начале круговой кривой эта бровка возвышалась над уровнем внутренней бровки на некоторую величину h₂. Чем больше длина отгона виража L, тем меньше уклон i₂, и тем плавней двухскатный профиль переходит в односкатный. Для дорог I и II категорий уклон i₂ не должен превышать 5 ‰, а для дорог III - V категорий - 10 ‰ в равнинной местности и 20 ‰ в горной.

Рисунок 5.27 — Преобразование проезжей части на отгоне виража

'

а) в начале отгона виража АОА₁; б) в конце отгона виража A'O'A₁'

Рисунок 5.28 — Поперечный профиль автодорожного полотна

Длина отгона виража L может быть подсчитана по формуле:

где b - ширина проезжей части дороги,

i₃ - поперечный уклон виража.

При устройстве отгона виража в пределах переходных кривых длина последних должна быть не менее величины L.

На виражах с радиусом кривых 700 м и меньше производят уширение проезжей части, величина которого приведена в таблице 5.3.

Таблица 5.3

Радиусы кривых, м	700 -500	500 -450	400 -250	200 -150	125 -90	80 -70	60	50	40	30
Уширение, м	0,40	0,50	0,60	0,75	1,00	1,25	1,40	1,60	1,80	2,00

Как правило, проезжую часть уширяют за счет уменьшения ширины внутренней обочины. Однако оставшаяся часть обочины должна быть не менее 1,5 м для дорог I и 11 категорий и на 1 м - для остальных, в противном случае уширяется земляное полотно.

В пределах круговой кривой виража проезжая часть уширяется на полную величину, на переходных кривых отгона уширение постепенно уменьшается. При этом внутренняя кромка полного уширения разбивается по кривой радиуса

где R - радиус кривой по оси дороги,

b - ширина проезжей части;

- полная величина уширения.

Разбивка кромки отвода уширения производится по плавной многоцентровой (коробковой) кривой.

На местности вираж разбивают путем построения поперечных профилей дорожного полотна через 5 – 10 м. До начала отгона виража обочинам придают уклон, равный уклону проезжей части, т. е. обе бровки полотна на протяжении 10 м поднимают на величину (рисунок 5.28, а):

где а - ширина обочины;

i₀- поперечный уклон обочины,

i₁ - поперечный уклон проезжей части на двухскатном профиле.

Поперечный профиль имеет вид АОА₁.

В конце отгона виража (в начале круговой кривой) дорожное полотно будет иметь односкатный уклон А'0'А₁' (см.рисунок 5.28, б).

При этом если вращение дорожного полотна осуществляется вокруг его внутренней кромки, то превышение характерных точек поперечного профиля относительно начального сечения без учета продольного уклона дороги будет:

- для осевой точки:

- для внешней кромки проезжей части полотна:

- для внешней бровки дорожного полотна:

- для внутренней бровки:

где - уширение проезжей части дороги,

i₃ - поперечный уклон виража.

Кроме этого, вследствие вращения около внутренней кромки происходит понижение высоты внутренней бровки на величину: Таким образом, общая величина изменения высоты внутренней бровки на вираже:

Превышения промежуточных поперечных профилей находят путем интерполирования величин, определенных, пропорционально расстоянию от начала отгона виража.

Решение задачи: расчет отметок точек на поперечнике с учетом

продольного уклона i₂.

Исходные данные: H - проектная отметка бровки полотна;

a, b, i₁, i₂, i₃, - размеры дороги, поперечные и продольный уклоны и величина уширения проезжей части дороги.

Для решения задачи используются следующие уклоны:

i₁ – поперечный уклон проезжей части;

i₂ – продольный уклон проезжей части;

i₃ – поперечный уклон виража;

i₀ – поперечный уклон обочины.

Решение задачи выполняется в следующей последовательности.

1) Отметки характерных точек на начальном поперечнике:

-отметка бровки с учетом подъема обочин на 20‰.

-отметка кромки:

-отметка оси дороги на начальном поперечнике:

2) С учетом продольного уклона трассы на отгоне виража и длины отгона виража можно вычислить отметку кромки дороги в конце отгона виража (в поперечном направлении отметка не изменяется, т.к. вращение выполняют вокруг ее оси):

От полученной отметки Н_кр.к вычисляют остальные отметки характерных точек.

3) Вычисляют отметки характерных точек на конечном поперечнике с учетом уширения проезжей части:

-отметка оси дороги на конечном поперечнике:

-отметка внешней кромки дороги на конечном поперечнике:

- отметка внешней бровки на конечном поперечнике:

- отметка внутренней бровки на конечном поперечнике:

Отметки характерных точек на промежуточных поперечниках определяется путем интерполирования.

При разбивке отгонов виража на смежных кривых, направленных в разные стороны, между ними необходимо иметь прямую вставку такой длины, чтобы в ее пределах можно было разместить встречные отгоны виража с поперечными уклонами противоположного направления (обычно 50-100 м).

На смежных кривых, направленных в одну сторону, но имеющих различные радиусы кривых и неодинаковые элементы виража, минимальная прямая вставка между ними должна быть такой длины, чтобы в ее пределах можно было вписать плавный переход одного виража к другому.

При трассировании дороги по крутому склону с острым внутренним углом нет возможности сопрягать прямолинейные участки при помощи общих закруглений.

В таких случаях, вследствие большой разности высот между началом и концом кривой и незначительной длины закругления, получаются уклоны, превышающие предельные. Сопряжение осуществляют при помощи внешних закруглений, называемых серпантинами (рисунок 5.29).

Основными элементами серпантина являются:

1) основная круговая кривая EFDC с радиусом R;

2) две вспомогательные кривые AP и BQ с радиусом r ;

3) две прямые вставки (или переходные кривые) QE и PF длиной m;

4)  - угол поворота вспомогательной кривой;

5) d - расстояние от вершины угла до поворота вспомогательной кривой;

6)  - угол в центре серпантина;

7) ₀ - центральный угол основной кривой;

8)  - угол поворота трассы в центре серпантина.

Размерные величины:

0. 1) наименьший радиус R = 1530 м;

1. 2) поперечный уклон виража 60 ‰

2. 3) длины переходных кривых 2030 м;

3. 4) удлинение проезжей части 23 м;

4. 5) продольный уклон i₂=3040 ‰

Рисунок 5.29 — Расчет элементов серпантина

При расчете серпантина обычно задаются величины R, r, а также величина m. Угол  измеряется в натуре на местности. Остальные элементы , , ₀,d вычисляют.

Угол поворота вспомогательной кривой  находится из прямоугольного треугольника ONF (или OME):

.

Так как OF = R, NF = m + T,

где T - длина тангенса вспомогательной кривой, то:

.

Из прямоугольного треугольника NPC:

Выполнив известные математические преобразования, получим уравнение:

Вычислив угол  и зная величину r вспомогательной кривой, по таблицам круговых кривых определяем T, Б, К - для вспомогательной кривой.

Из треугольника ONF находят расстояние от вершины N вспомогательной кривой до центра О основной кривой:

ON = d = R/ sin.

Для контроля d вычисляют по формуле:

d = (m + T)/ cos.

Угол в центре серпантина, определяющий направление на начальную и конечную точки основной кривой, определяется по формуле:

 = 90 - ,

а центральный угол основной кривой:

₀ =360 -2 - .

Длина основной кривой:

При разбивке серпантина теодолит устанавливают в вершине угла поворота О и по створу направлений ОА и ОВ откладывают величину d, получив на местности точки M и N -вершины вспомогательных кривых.

Отложив от этих точек по створу ОА и ОВ длину Т, находят точки А и В (начало и конец серпантина). От сторон ОА и ОВ откладывают угол  вправо и влево, и вдоль полученных направлений, отложив длину R, получают точки E и F (начала и конца основной кривой).

Детальную разбивку основной кривой производят через 35 м. Для этого угол ₀ делят на соответствующее количество углов и по заданным направлениям откладывают радиусы R основной кривой.

Затем с теодолитом переходят в точку М (или N), от направления МО (NO) откладывают угол  и в этом направлении откладывают величину Т, получают точку Q (P) - конец вспомогательной кривой. Для контроля измеряют угол OEF, который должен быть равен вычисленному ₀. Расчет пикетажа для основных точек серпантина выполняют в следующем вычислительном формуляре:

ПК «0» -d + T1	Контроль:
ПК НС (т. А) +1/2 Кb1	ПК КС - (2Кb + 2m + K)
ПК КВК1 + m	ПК НС
ПК НОС + 1/4ОК + 1/4ОК
ПК СОК + 1/4ОК + 1/4ОК
ПК КОК + m
ПК НВК2 + 1/2 Кb2
ПК СВК2 +1/2 Кb2
ПК КС

Рисунок 5.30 — Расчет пикетажа серпантина

Для расчета ширины участка в самом узком месте серпантина Z_c (рисунок 5.31) запишем следующее выражение:

Рисунок 5.31 — Расчет ширины участка в самом узком месте серпантина

где h - превышение верхнего полотна автомобильной дороги над нижним;

i - уклон местности по линии M'N'.

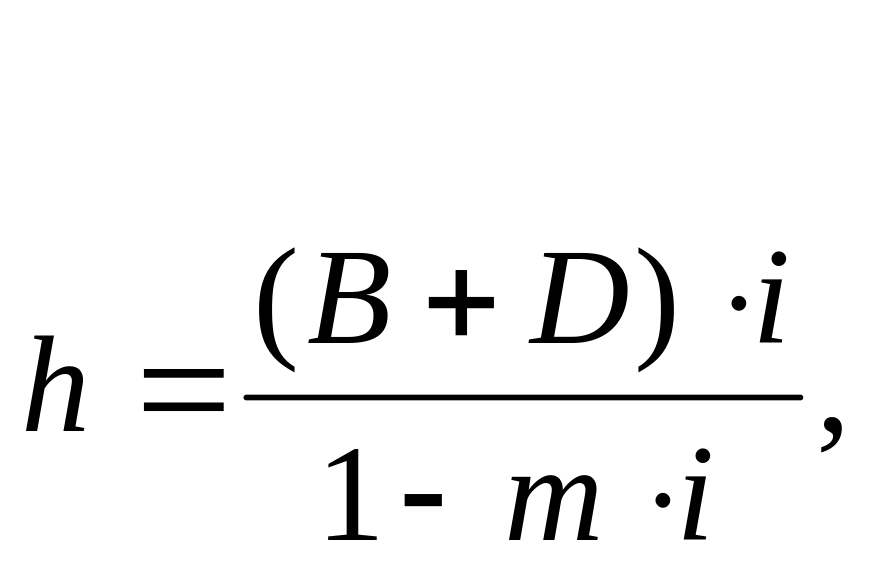
тогда, получим:

Считается, что дорога запроектирована правильно, если Z_c  Z_g.

Продольный профиль серпантина строится по отметкам характерных точек оси серпантина (рисунок 5.32).

Рисунок 5.32 — Продольный профиль серпантина

Проектирование красной линии выполняется с соблюдением условий минимума баланса земляных работ в пределах допустимых продольных уклонов.

Запроектировав проектную ось серпантина, вычисляют проектные (красные отметки) характерных точек серпантина. Рекомендуется при проектировании проектного положения оси серпантина на прямых вставках и вспомогательных кривых максимально приближаться к существующему рельефу.

Зная проектные отметки оси серпантина, можно построить поперечники (рисунок 5.33). Их используют для определения положения подошвы насыпи и бровки выемки.

На листе миллиметровой бумаги приблизительно по середине проводим вертикальную линию. От нее вправо и влево в соответствующем масштабе откладываем 1/2В (половину ширины дороги) и ширину кювета Д. Слева от поперечника оцифровываем масштабную линейку отметок. По осевой линии строят проектную отметку и черную отметку для соответствующей точки. Затем, зная параметры дороги, достраивают остальной профиль поперечника.

После завершения работ по построению поперечников, строят план серпантина М 1:500 (рисунок 5.34).

Первоначально на плане уже имеется нанесенная ось дороги на серпантине. Откладывая вправо и влево от оси дороги В/2 в масштабе плана, строят план дороги. Затем, используя поперечники, достраивают на плане кюветы, насыпи и выемки. Для этого используют размеры S₁ и S₂, взятые с поперечников. Если это выемка, то достраивают еще полосу кюветов.

Рисунок 5.33 — Продольный профиль серпантина

Для построения точки перехода от насыпи к выемки и наоборот, на продольном профиле между соответствующими поперечниками дополнительно строят линию внешней бровки и линию внутренней бровки (получаем точку пересечения с проектной линией).

Расстояние S₃ - расстояние от точки пересечения профиля внешней бровки с проектным профилем оси дороги до ближайшего пикета или характерной точки. Это расстояние S₃ используют при построении плана серпантина.