5 Геодезические работы при строительстве линейных сооружений

5.1 Полевое трассирование

Вынос трассы в натуру выполняется по данным привязки углов поворота трассы к пунктам геодезической основы или ближайшим четким контурам. Данные для привязки получают графическим путем с топографической карты.

После выноса в натуру положения соседних углов поворота трассы в створе устанавливают ряд вех, обследуют вынесенное направление (особенно переходы через овраги, пересечение автомагистралей и т.п.). При этом угол поворота и провешенную линию можно несколько смещать для обеспечения уменьшения объемов земляных работ. Окончательные вершины закрепляют на местности. При выносе трассы на местность может возникнуть ситуация, когда нет прямой видимости между двумя углами поворота, тогда для измерения углов можно применять следующие методики:

1) направление трассы получить от направления на пункт геодезического обоснования;

1, 2, 3 – точки теодолитного хода; II – точка полигонометрического хода

Рисунок 5.1 — Разбивка трассы от стороны теодолитного хода

2) от стороны хода, проложенного между соседними углами поворота трассы;

3) координаты точек, необходимые для вычислений, снимают графически с плана;

4) по точке С, приблизительно намеченной в створе соседних вершин поворота.

Рисунок 5.2 — Разбивка трассы от линии створа

Измеряют . Затем вычисляют угол , отложив который от направления АС, определяют положение створа АВ.

Определив направление трассы между углами поворота, устанавливают дополнительные створные точки и производят по трассе угловые и линейные измерения, нивелируют трассу по пикетажу.

При трассировании измеряют правые по ходу углы 1, 2, 3 ,..., n, а углы поворота трассы вычисляют по формулам:

Рисунок 5.3 — Схема измерения углов для определения углов поворота

При трассировании выполняют два вида линейных измерений:

- расстояния между углами вершин поворота и створными точками измеряют чаще всего светодальномером и используют для вычисления координат углов поворота трассы;

- расстояния, необходимые для разбивки пикетажа, круговых кривых, для поперечных профилей и т.д. выполняют рулеткой или металлической измерительной лентой.

Измерение длин совмещают с разбивкой пикетажа (отрезков по 100 м). В 100 м вводят поправку за наклон:

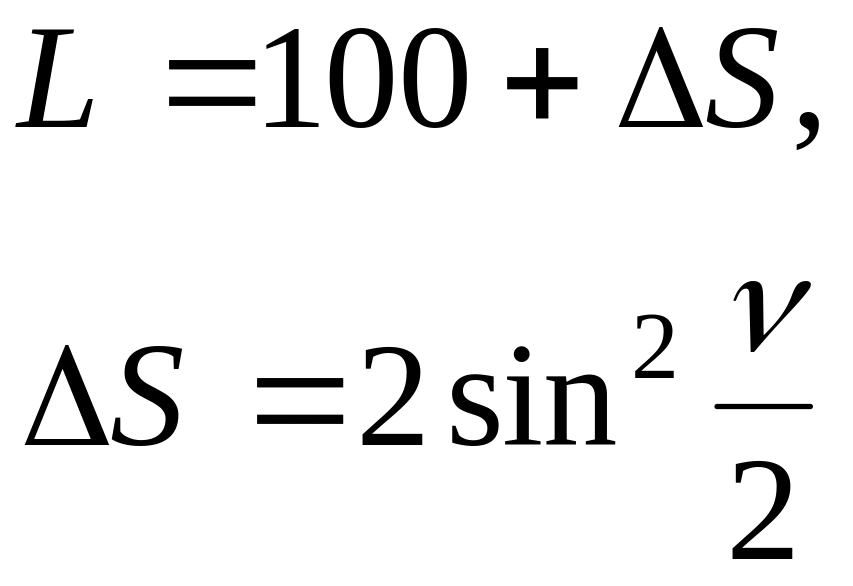, при >2 градусов.

Одновременно с разбивкой пикетажа по оси трассы фиксируют характерные точки рельефа и точки ситуаций. Расстояния до этих точек измеряют от предыдущего пикета (рисунок 5.4).

Рисунок 5.4 — План разбивки трассы

Рисунок 5.5 — Основные элементы кривой

При подходе к углам поворота производят вставку кривой и пикетаж считают по кривой (длина трассы определяется по прямым вставкам и кривым).

Радиус кривой задается в проекте и зависит от категории дороги, а также от угла поворота трассы. Угол поворота трассы снимают с плана и определяют из таблицы 5.1, элементы круговой кривой: Т, К, Д, Б (рисунок 5.5).

Пикетаж начала и конца кривой вычисляют по формулам:

ПКНК=ПКВУ-Т; ПККК=ПКНК+К; ПКСК=ПКНК+К/2.

Контроль: ПККК=ПКВУ+Т-Д.

При разбивке пикетажа ведут пикетажный журнал, в котором показывают ось трассы в виде прямой линии, на которую наносят в масштабе все пикетажные и плюсовые точки, границы препятствий и ситуацию.

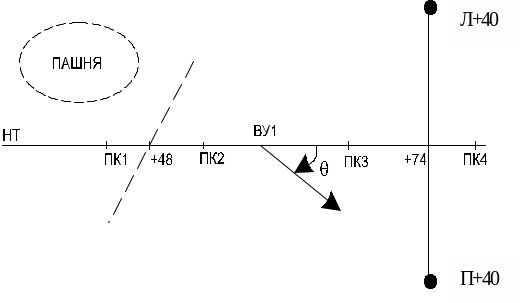
Рисунок 5.6 — Фрагмент пикетажного журнала

Запись ведется снизу вверх, чтобы левая и правая стороны страницы соответствовали левой и правой стороне трассы. Углы поворота показывают в виде стрелок, подписывают пикетаж начала и конца круговых кривых, записывают элементы круговых кривых.

Для представления о рельефе вдоль трассы по ее ширине на косогорных участках разбивают поперечники, т.е. по обе стороны трассы на расстоянии 15 -20 м (в зависимости от характера склона и типа трассы) определяют отметки и строят поперечные профили. Поперечники назначают на таком расстоянии друг от друга, чтобы местность между ними имела однообразный уклон. Если уклон больше , то поперечники разбивают на всех пикетажных и плюсовых точках.

Переходные кривые строят в том случае, если R<2000 м. При переходе автомобиля с прямолинейного участка на криволинейный и обратно возникает мгновенное изменение центробежной силы от 0 до F:

где V - скорость движения;

Р - вес автомобиля;

g - ускорение силы тяжести;

R- радиус круговой кривой.

При большой скорости движения, малом радиусе, большой массе автомобиля получают значительный удар колес автомобиля о дорожное покрытие. Чтобы избежать этих явлений на дорогах устраивают переходные кривые, имеющие переменный радиус кривизны от ∞ на прямолинейном участке, до R на криволинейном участке. В результате удар заменяется последовательным увеличением давления колес на дорожное покрытие.

Переходные кривые (длиной l) строят наполовину за счет круговой кривой и половину за счет прямого участка. В результате, кривая удлиняется за счет переходных кривых, угол на участке кривой уменьшается на величину: ,

где .

Устройство переходных кривых возможно только в том случае, когда > . В этом случае между концом и началом переходной кривой будет располагаться участок круговой кривой. При равенстве этих элементов конец переходной кривой будет началом второй переходной кривой. Перекрытие между собой этих переходных кривых недопустимо.

Рисунок 5.7 — Схема круговой кривой с переходными кривыми:

L – длина переходной кривой (ПК); t (или m) – приращение тангенса Т при устройстве ПК; р – величина сдвижки круговой кривой (КК) при устройстве ПК; Т_р – приращение тангенса КК, вызванное сдвижкой р; Б_р – приращение биссектрисы, вызываемой сдвижкой р

Между радиусом круговой кривой R и длиной переходной кривой l существует зависимость, представленная в таблице 5.1.

Таблица 5.1

R,м	30	50	60	80	100	150	200	250	300	400	500	600-2000
l,м	30	35	40	45	50	60	70	80	90	100	110	120

Чтобы рассчитать элементы смещения кривой, необходимо уменьшить радиус круговой кривой на величину сдвижки Р, но как правило, радиус не уменьшают, а сдвигают центр круговой кривой на величину Б_р (рисунок 5.7). Элементы переходной кривой берут из таблиц или вычисляют по формулам:

Тск	=	Ткк + ΔТ ,
ΔТ	=	t + Тр
Тр	=	Р * tg	φ
			2
t	=	l / 2
P	=	l2
		24 R
Бр	=	p* sek		φ
				2

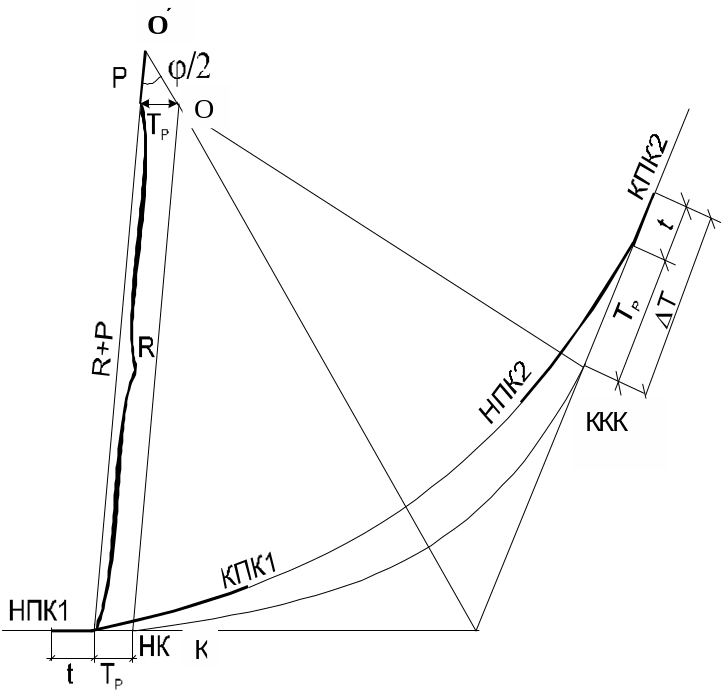
Рисунок 5.8 — Схема переходных кривых

где индекс “ск”- смещенная кривая.

Расчет пикетажа с учетом переходных кривых выполняется по формулам:

- начало кривой смещения - ПКН3(НКс)=ПКВУ-Тск ;

- конец переходной кривой 1 - ПККПК1=ПКН3(НК1)+l;

- конец кривой смещения - ПКК3(ККс)=ПКН3+Кс;

- контроль: ПКК3(ККс)=ПКВУ+Тск-Дск.

При проектировании трассы переломы в вертикальной плоскости сопрягают вертикальными кривыми (рисунок 5.9).

Рисунок 5.9 — Схема вертикальной кривой

Вертикальные кривые проектируют в случае, если выполняется следующее условие:

При трассировании пикетаж разбивают по тангенсам, поэтому возникает необходимость построения кривой на местности (вынесение проектного положения точек с касательных). Существует несколько способов детальной разбивки кривых.

Первый способ - способ прямоугольных координат.

За ось абсцисс принимают линию тангенса (касательную), за начало координат – начало кривой. Задавшись удалением К промежуточной точки кривой от начала координат, находят центральный угол  по формуле:

,

а по нему вычисляют прямоугольные координаты точек 1, 2, …, n по формулам:

где i – текущий номер точки кривой.

Рисунок 5.10 — Вынос точек с касательной на кривую способом прямоугольных координат

Вместо абсциссы часто пользуются величиной (К – Х) – кривой без абсциссы. Величины (К – Х) и у даются в таблицах и выбираются по аргументу К.

Для разбивки точки сначала откладывают вдоль касательной величину К, а затем, отступив назад на величину (К – Х), фиксируют временную точку и строят в ней перпендикуляр. На нем откладывают ординату у, в конце которой закрепляют точку кривой.

Данный способ применяется для разбивки круговых и переходных кривых, особенно в тех случаях, когда кривая близко подходит к тангенсу, а также при выносе пикета на кривую.

Второй способ - способ углов.

В этом способе используется то положение, когда углы с вершиной в какой-либо точке круговой кривой, образованные касательной АМ(Т) и соответствующей секущей, равны половине соответствующего центрального угла. Данный способ заключается в построении угла /2 в начале системы координат и последовательном откладывании хорды. При заданной длине хорды угол  определяют по формуле:

,

где в – длина хорды.

Для разбивки промежуточных точек кривой теодолит устанавливают в НК или КК, ориентируют его по линии тангенса и откладывают от этой линии угол /2 . Отложив вдоль построенного направления хорду l, закрепляют первую точку (В). Затем в той же точке НК строят угол 2/2 и откладывают хорду (В-С), получая на пересечении направления угла и хорды точку 2, и т.д. (рисунок 5.11).

Линейные измерения выполняют вблизи кривой, что выгодно при разбивке точек на насыпи. Этот способ применяют для разбивки кривых земляных сооружений.

Порядок выполнения разбивки следующий:

1) Выбирают из таблиц по радиусу угол в зависимости от величины b (b=10,20,30 м).

2) Устанавливают теодолит в точку А и от линии АМ фиксируют направление под углом .

3) Вдоль этого направления откладывают длину хорды b и закрепляют на местности точку.

4) Из точки А от направления АМ фиксируют следующее направление под углом и вдоль него откладывают длину хорды. В такой последовательности выполняют разбивку всей кривой.

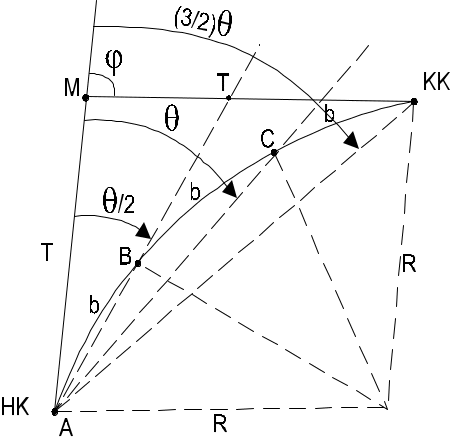
Рисунок 5.11 — Детальная разбивка кривой способом углов

3 способ - способ продолженных хорд (рисунок 5.11).

Задавшись длиной хорды, например 10 м, определяют смещение:

;

где b = 10 м (принятая длина хорды).

Рисунок 5.12 — Детальная разбивка кривой способом продолженных хорд

При помощи вычисленной величины смещения а разбивают все точки кривой, кроме первой точки. Первую точку получают по прямоугольным координатам хв и у=а/2 (рисунок 5.12). Протянув через НК (точка А) и точку 1 мерный прибор или трос длиной 2в, например рулетку, на продолжении получают предварительную точку 2’. Для получения на кривой точки 2 рулетку придерживают в точку 1, а ее конец сдвигают к кривой на величину а и фиксируют точку 2. Точку 3 получают аналогично на основе линии 1-2 и т.д. до середины кривой.

Разбивку кривой выполняют без теодолита, по радиусу кривой и по величине хорды b, из таблиц выбирают d и y. Положение первой точки может быть определено с помощью прямоугольных координат x и y или линейной засечкой.

Закрепив первую точку, на продолжении створа А1 откладывают длину хорды с и отрезок С-2=d. Точку 2 получают линейной засечкой (1-2=b, C-2=d) и т.д.

Этот способ применяется в стесненных условиях при невысокой точности разбивки (в насыпи, выемке).

Для детальной разбивки кривых на практике применяются также способ трех точек, способ вписанного многоугольника.

Ежедневно проверяются полевые журналы, обращают внимание на правильность углов поворота. Производят уравнивание нивелирных и теодолитных ходов.

Допустимая угловая невязка вычисляется по формуле:

где n - число сторон.

Относительная невязка не должна превышать по ходу 1/1000.

Производят вычисление координат и высот пикетов, составляют ведомость прямых и кривых, в которых выполняются контроли:

- разность между и должна быть равна :

- разность между суммами правых и левых углов поворота равны разности дирекционных углов конечной и начальной точек трассы:

- сумма прямых вставок и кривых равна длине трассы:

- разность пикетажных значений конца и начала трассы равна длине трассы:

- разность суммарного значения всех расстояний между углами поворота и суммой всех домеров:

Составляют план трассы в масштабе 1:10 000 или 1:5000 по координатам углов поворота или по азимутам и длинам сторон. На план наносят знаки крепления трассы, начало и конец трассы, километровые пикеты, на закруглениях подписывают элементы кривых, на прямых вставках подписывают длину и азимут. Составляют продольный профиль трассы.