3. Задание

Объектом исследования является нагруженная по верхней поверхности равномерно распределённой поперечной нагрузкой интенсивностью q прямоугольная в плане, шарнирно опёртая по контуру плита со сторонами a, b и толщиной h (рис. 6), модулем упругости E и коэффициентом Пуассона ν материала.

Рис.6. М.1:35

Разрешающую функцию принять в виде двойного тригонометрического ряда

(24)

В этом случае условия на контуре (23) удовлетворяются, а дифференциальное уравнение (20) обращается в тождество, если коэффициенты ряда будут равны

(25)

где

Для постоянной нагрузки ( )

,	(26)
	(27)

где так как чётные члены ряда (24) обращаются в нуль.

Коэффициенты находятся по формуле

(28)

с параметро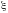м , равным

(29)

Тогда, подставляя функцию (27), например в (11), получим следующие выражения для изгибающих моментов:

(30)

где

(31)

Требуется:

найти прогиб в точке плиты A с координатами ;
определить наибольшие нормальные напряжения 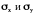в сечении, проходящем через точку A;
в вычислительной лаборатории кафедры произвести поверочный расчёт на ПЭВМ и представить протокол расчёта (студенты заочной формы обучения выполняют этот пункт по желанию);
по полученным на ПЭВМ результатам найти наибольшие касательные напряжения в заданном сечении.

При вычислениях вручную следует удерживать только те члены ряда, величина которых равна или превышает 5% от первого члена ряда.

4. Рекомендции по выполнентю работы

4.1. Исходные данные

Выписать заданные; размеры плиты ; интенсивность равномерно распределённой нагрузки q; модуль упругости E и коэффициент Пуассона ν материала; координаты расчётного сечения.