5.2.2Геометрическое изображение системы ограничений.

Линия уровня линейной функции.

Выше говорилось, что множество допустимых решений (многогран­ник решений) задачи линейного программирования представляет со­бой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи находится, по крайней мере, в одной из угловых точек многогранника решений.

Рассмотрим задачу в стандартной форме с двумя переменными (n = 2). К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2, т.е. n - m = 2.

Пусть геометрическим изображением системы ограничений явля­ется многоугольник ABCDE (рис. 2.1). Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F=c₁x₁ + c₂x₂ принимает максимальное (или минимальное) значение.

Рассмотрим так называемую линию уровня линейной функ­ции F, т.е. линию, вдоль которой эта функция принимает одно и то же фиксированное значение а, т.е. F = а, или

. (5.2.1)

На многоугольнике решений следует найти точку, через которую проходит линия уровня функции F с наибольшим (если линейная функ­ция максимизируется) или наименьшим (если она минимизируется) уровнем.

Уравнение линии уровня функции (5.2.1) есть уравнение прямой линии. При различных уровнях а линии уровня параллельны, так как их угловые коэффициенты определяются только соотношением между ко­эффициентами с₁ и с₂ и, следовательно, равны. Таким образом, линии уровня функции F - это своеобразные "параллели", расположенные под каким-то углом к осям координат.

F = F_max

B C

F = F_min

F = 0

D

A

E F = a

0

Рисунке 5.2.1

Важное свойство линии уровня линейной функции состоит в том, что при параллельном смешении линии в одну сторону уровень только возрастает, а при смещении в другую сторону только убывает.

Пусть имеются три линии уровня:

F = c₁x₁ + c₂x₂ = a₁ (I),

F = c₁x₁ + c₂x₂ = a₂(II),

F = c₁x₁ + c₂x₂ = a₃(III),

причем линия II заключена между линиями I и II. Тогда a₁ < a₂ < a₃ или a₁>a₂>a₃.

В самом деле, на штриховой линии - (перпендикулярной к линиям уровня, (рис. 5.2.2) уровень является линейной функцией, а значит, при смещении в одном из направлений возрастает, а в другом - убывает.

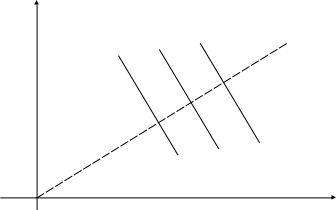Х ₂

III

I II

F = a

F = a₁ F = a₂

0 Х ₁

Рисунке 5.2.2

Для определения направления возрастаниия рекомендуется изоб­разить две линии уровня и определить, на которой из них уровень боль­ше. Например, одну из линий можно взять проходящей через начало координат (если линейная функция имеет вид F = с₁х₁ + с₂х₂, т.е. без свободного члена, то это соответствует нулевому уровню). Другую линию можно провести произвольно, так, например, чтобы она проходи­ла через множество решений системы ограничений. Далее, определив направление возрастания линейной функции (обозначим его вектором q), найдем точку, в которой функция принимает максимальное или ми­нимальное значение (на рис. 2.1 - это точка С или А).

Этапы решения задачи

Таким образом, геометрически задача линейного программиро­вания представляет собой поиск такой точки многогранника решений, координаты которой доставляют линейной функции наибольшее (наи­меньшее) значение, причем допустимыми решениями являются все точки многогранника решений.

Графический метод решения задачи линейного программирова­ния состоит из следующих этапов.

Этап 1. Сначала на координатной плоскости х₁Oх₂, строится допус­тимая многоугольная область (область допустимых решений, область определения), соответствующая ограничениям. Далее строится вектор q, координаты которого являются частными производными функции F. Вектор показывает направление возрастания линейной функции F в ка­кой-нибудь точке X₀, принадлежащей допустимой области.

Этап 2. Прямая F = c₁x₁ + c₂x₂, перпендикулярная вектору q, передвигается в направлении этого вектора в случае максимизации F до тех пор, пока не покинет пределов многоугольной области. Предельная точка (или точки) области при этом движении и является точкой макси­мума F.

Этап 3. Для нахождения координат точки максимума достаточно решить два уравнения прямых, получаемых из соответствующих огра­ничений и дающих в пересечении точку максимума. Значение F, най­денное в получаемой точке, является максимальным.

В случае минимизации F прямую F = c₁x₁ + c₂x₂ надо двигать в направлении, противоположном вектору q. Ясно, что если прямая F = с₁х₁ + c₂x₂ при своем движении не покидает допустимой области, то соответствующий максимум или минимум F не существует.

Рассмотрим пример. Решить графическим методом следующую задачу:

F = 30 x₁ + 60 x₂ max

при ограничениях:

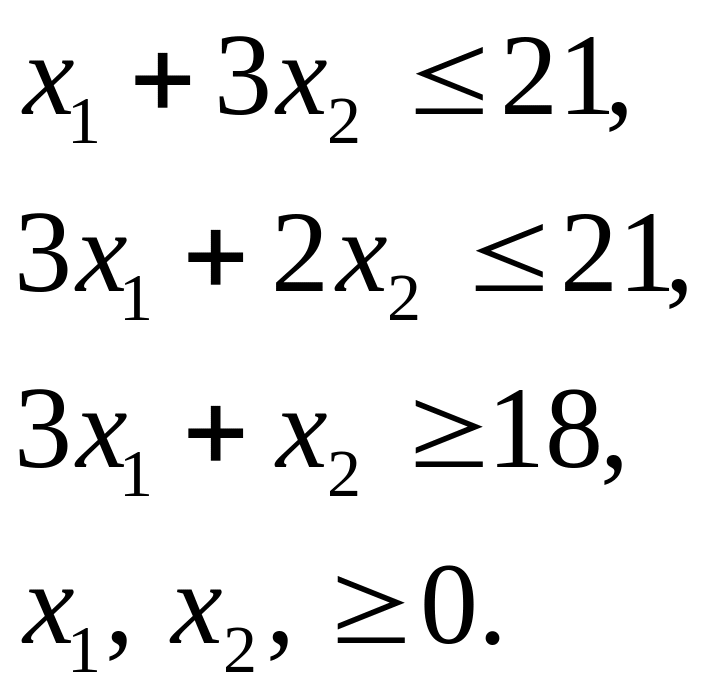
Прямые ограничения х₁, х₂  0 означают, что область решений бу­дет лежать в первой четверти декартовой системы координат; отметим штриховкой эту область на рисунке 5.2.3.

Этап 1. Определим множество решений первого неравенства. Оно состоит из решения уравнения и строгого неравенства. Решением урав­нения служат точки прямой х₁ + Зх₂ - 21 = 0. Построим прямую по двум точкам (0; 7) и (21; 0), которые легко получить в результате последователь­ного обнуления одной из переменных. На рисунке обозначим ее циф­рой I.

Множество решений строгого неравенства - одна из по­луплоскостей, на которую делит плоскость построенная прямая. Какая из них является искомой, можно выяснить при помощи одной конт­рольной точки. Если в произвольно взятой точке, не принадлежащей прямой, неравенство выполняется, то оно выполняется и во всех точ­ках той полуплоскости, которой принадлежит контрольная точка, и не выполняется во всех точках другой полуплоскости. В качестве такой точки удобно брать начало координат. Подставим координаты (0; 0) в неравенство, получим -21 < 0, т.е. оно выполняется. Следовательно, областью решения неравенства служит нижняя полуплоскость.

Аналогичным образом построим области решения двух других неравенств:

3x₁ + 2x₂ – 21 = 0;

x₁ = 0, x₂ = 10,5;

x₂ = 0, x₁ = 7.

(на рисунке прямая II);

3x₁ + 2x₂ – 21 < 0 при х₁ = х₂ = 0, – 18 < 0 выполняется, берётся нижняя полуплоскость.

Заштрихуем общую область для всех неравенств, обозначим вершины многоугольника латинскими буквами и определим их координаты, решая систему уравнений двух пересекающихся соответствующих прямых. Например, определим координаты точки С, являющейся точкой пересечения второй и третьей прямой:

3x₁ + 2x₂ = 21, x₂ = 3, x₁ = 5,

3x₁ + x₂ =18.

Вычислим значение целевой функции в этой точке:

F = 30x₁ + 60x₂ = 150 + 180 = 330.

Аналогично поступим для других точек, являющихся вершинами замкнутого многоугольника OABCD, представляющего собой область допустимых решений рассматриваемой задачи. Координаты этих вершин имеют следующие значения: O (0;0), A (0;7), B (3;6), C (5;3), D (6;0).

Этап 2. Приравняем целевую функцию постоянной величины а: 30х₁+60х₂ = а.

Это уравнение является множеством точек, в котором целевая функция принимает значение, равное а. Меняя значение а, получим семейство параллельных прямых, каждая из которых называется линией уровня. Пусть а=0, вычислим координаты двух точек, удовлетворяющих соответствующему уравнению 30х₁ + 60х₂. В качестве одной из этих точек удобно взять точку О (0;0), а так как при х₁ = 2х₂ = 0, то в качестве второй точки возьмём точку G (2; -1).

Через эти две точки проведём линию уровня F = 30x₁ + 60x₂ = 0 (пунктирная прямая на рис. 5.2.3).

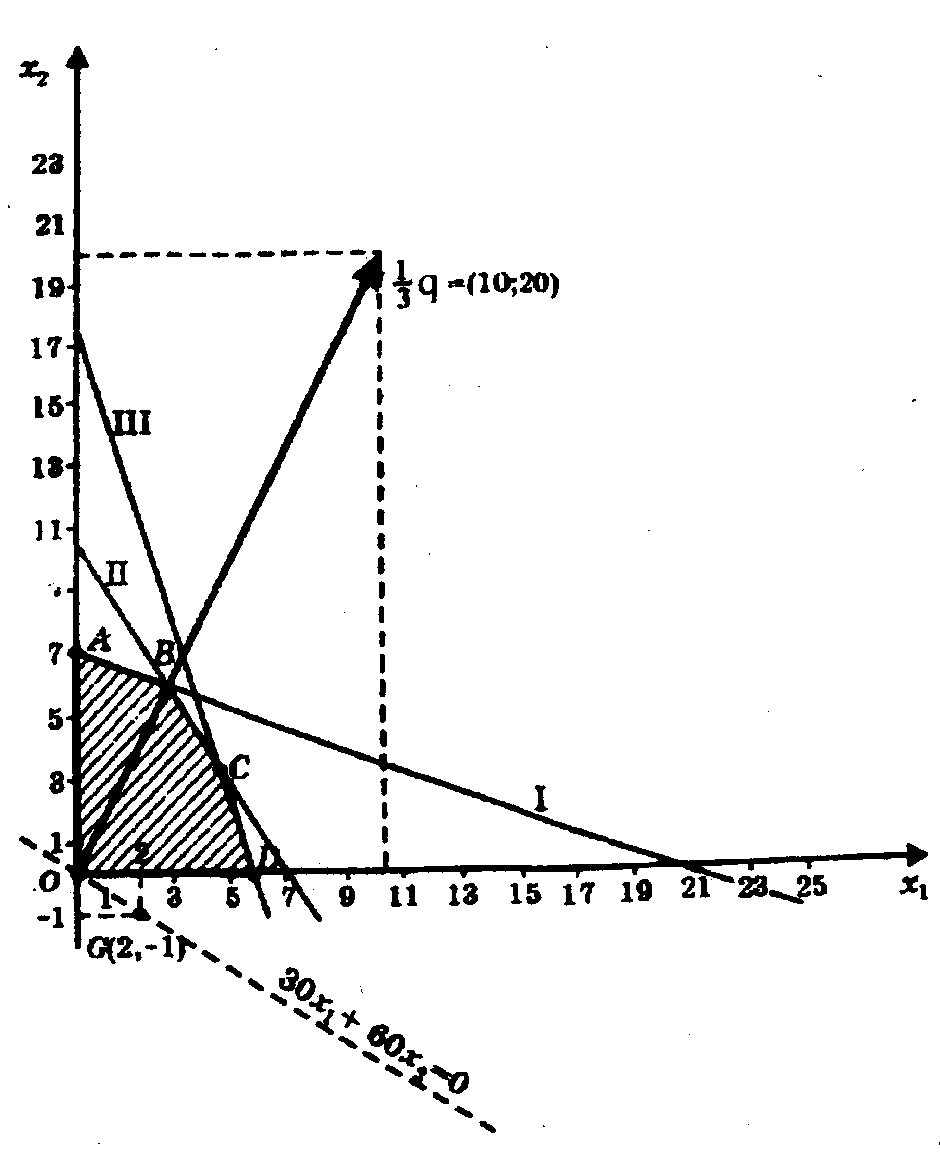
Рисунке 5.2.3

Этап 3. Для определения направления движения к оптимуму пост­роим вектор q, координаты которого являются частными производны­ми функции F, т.е. q = (30;60).

Чтобы построить этот вектор, нужно соединить точку (30;60) с нача­лом координат. При максимизации целевой функции необходимо дви­гаться в направлении вектора q, а при минимизации - в противо­положном направлении. Для удобства можно строить вектор, пропор­циональный вектору q. Так, на рисунке 5.2.3 изображен вектор 1/3 q= (10;20).

В нашем случае движение линии уровня будем осуществлять до ее пересечения с точкой В; далее она выходит из области допустимых решений. Следовательно, именно в этой точке достигается максимум целевой функции. Отсюда легко записать решение исходной задачи линейного программирования : max F = 450 и достигается при х₁ = 3; x₂ = 6.

Если поставить задачу минимизации функции F = 30x₁ + 60x₂ при тех же ограничениях, линию уровня необходимо смещать параллельно самой себе в направлении, противоположном вектору q. Как это видно на рисунке 5.2.3, минимум целевой функции достигается в точке 0 (0;0), следовательно, можно записать min Х = 0 и достигается при х₁ = 0; x₂ = 0.

При решении некоторых задач линейного программирования гра­фическим методом может встретиться случай, когда линия уровня па­раллельна одной из сторон выпуклого многоугольника допустимых ре­шений, причем эта сторона расположена в направлении смещения ли­нии уровня при стремлении целевой функции к своему оптимуму. В этом случае оптимальное значение целевой функции достигается не в одной, а в двух угловых точках (вершинах) многоугольника решений и, следовательно, во всех точках отрезка, соединяющего эти вершины, т.е. задача будет иметь бесчисленное множество решений.

Если область допустимых решений является незамкнутым выпук­лым многоугольником в направлении оптимизации целевой функции, то целевая функция будет неограниченной и задача линейного про­граммирования не будет иметь решений.

Очевидно также, что задача линейного программирования не бу­дет иметь решений в случае, когда область допустимых решений есть пустое множество, т.е. система ограничений задачи линейного про­граммирования содержит противоречивые неравенства и на коорди­натной плоскости нет ни одной точки, удовлетворяющей этим ограни­чениям.

Рассмотренный в этой главе геометрический метод решения за­дач линейного программирования обладает рядом достоинств. Он прост, нагляден, позволяет быстро и легко получить ответ.

Однако только геометрический метод решения никак не может удов­летворить ни математиков, ни экономистов. Возможны "технические" погрешности, которые неизбежно возникают при приближенном пост­роении графиков. Второй недостаток геометрического метода заклю­чается в том, что многие величины, имеющие четкий экономический смысл (такие как остатки ресурсов производства, избыток питательных веществ и т.п.), не выявляются при геометрическом решении задач. Но самое главное - геометрический метод неприемлем для решения прак­тических задач. Его можно применить только в том случае, когда число переменных в стандартной задаче равно двум. Поэтому необходимы: аналитические методы, позволяющие решать задачи линейного программирования с любым числом переменных и выявлять экономичес­кий смысл входящих в них величин. Эти методы будут рассмотрены в следующих главах.