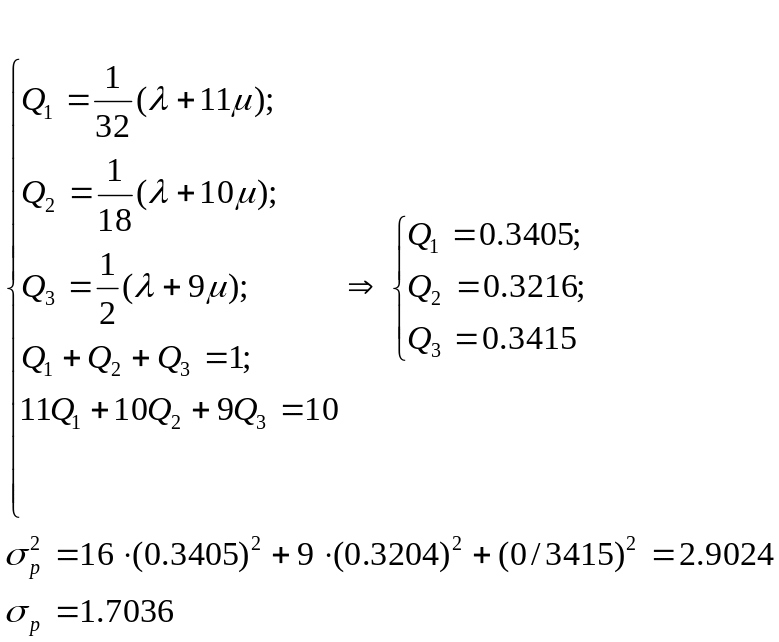3. Риски и их измерители

3.1. Методы уменьшения финансового риска

В ранее рассматриваемых финансовых операциях все существующие показатели являются детерминированными величинами. На самом же деле все финансовые операции являются рисковыми в том смысле, что их эффективность является недетерминированной, т. е. неизвестной на момент сделки. В наибольшей степени это относится к операциям купли-продажи ценных бумаг. Степень неопределенности риска можно измерить, исходя из предположения, что эффективность операции R является связью, а наблюдаемое её значение r – это всего лишь отдельная реализация R. В этом случае под риском понимается вероятность любого нежелательного события, например, вероятность разорения. В какой-то степени неопределенность характеризуется дисперсией, а, следовательно, и риск разорения:

D(х)= ,

σ_x= .

Чем меньше дисперсия, тем меньше неопределенность. Из двух финансовых операций

R₁ и R₂

MR₁=m₁ ,

MR₂=m₂ ,

m₁<m₂

σ₁<σ₂

Любая из мер снижения риска называется хеджированием. Покупая акции одной компании, инвестор ставит себя в зависимость от колебания курсов ее акций. Если же он размещает свои инвестиции в капитале нескольких компаний, то эффективность сформированного таким образом портфеля ценных бумаг будет зависеть от средневзвешенной дисперсии. В некоторых случаях такая дисперсия может быть меньше, чем дисперсия акций отдельных элементов, что приводит к снижению неопределенности.

3.2. Оптимизация портфеля ценных бумаг

Пусть мы имеем портфель ценных бумаг из n-составляющих, эффективность каждого i-го равняется R_i c M_Ri = m_i и D_Ri = σ_i².

Матрица ковариации представляет собой матрицу, состоящую из коэффициентов ковариации между отдельными видами эффективности ценных бумаг.

B=||cov(R_i, R_j)||

cov(R_i, R_j)=DR_j

Коэффициент ковариации показывает степень тесноты связи между двумя случайными процессами. Если коэффициент ковариации равен 1, то случайные процессы имеют очень тесную связь между собой.

Если коэффициент корреляции r =-1, то связь тоже очень тесная, но обратно, если r =0, то связи нет.

Инвестор распределяет свой капитал Q_j.

0 ≤ Q _i≤ 1

Эффективность формирования портфеля R_p

R_p= .

Такая связь имеет математическое ожидание

MR_p=M( .

Портфельная дисперсия

.

Соотношения между Q_i называются структурной составляющей портфеля ценных бумаг. Оставив за инвестором право выбора средней эффективности, поможем ему минимизировать неопределенность; исходя из этого, получаем систему уравнений

min ;

b_i,j=cov(R_i,R_j);

- уравнение эффективности.

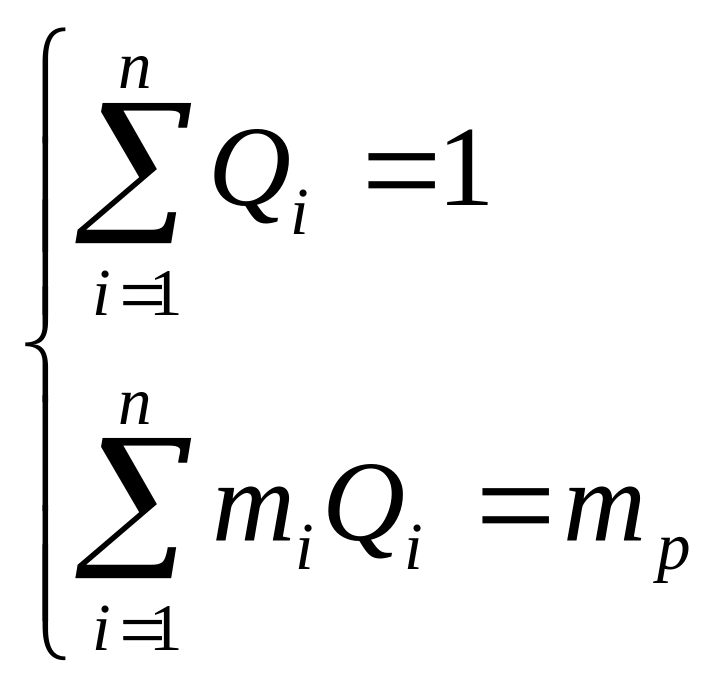, Q_i≥0

- система ограничений, где m_p – выбранное значение эффективности портфеля.

Математически данная задача предусматривает собой минимизацию квадратичной формы от n переменных Q_i, связанных между собой соотношениями и условиями; которая решается методами квадратичного программирования. Если не рассматривать условие, получаем задачу Марковица, решение которых рассмотрим ниже:

L(Q₁, …Q_n, λ, μ)= ;

, l=1,n (*).

Производные по λ и μ приводят к системе ограничений, следовательно, для разрешения выражения (*) получаем систему из n+2 уравнений. Запишем полученное уравнение в матричной форме:

e= ; Q= ; m= ;

m^T=(m₁…m_n);

Q^T=(Q₁…Q_n)

Уравнение Лагранжа примет вид:

Предположим, что между эффективностями R₁ …R_n нет линейной связи, следовательно, ковариационная матрица В не вырождена, т.е. ее определитель Δ ≠ 0 и, следовательно, существует В^-1. Используя это обстоятельство, решим уравнение в матричной форме

Q= . (*)

Подставим данное выражение в условие ограничений

Решая систему уравнений методом Кремера, находим:

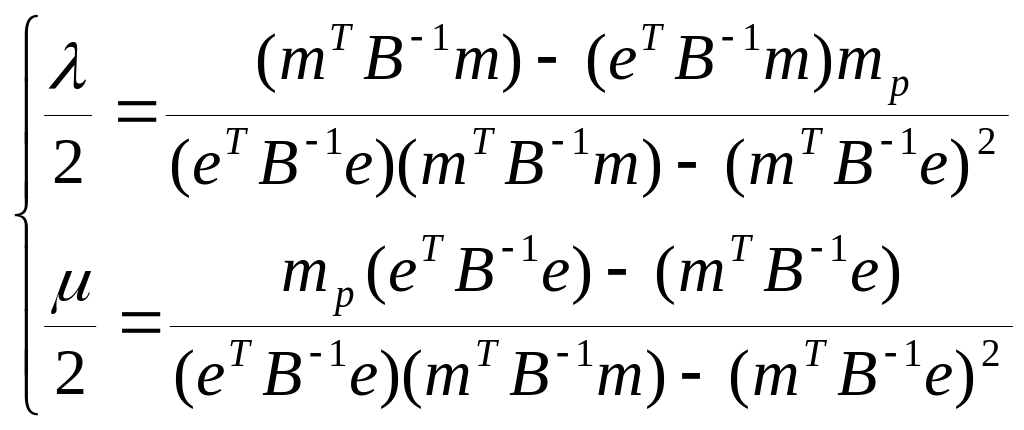
Подставив это решение в выражение для Q(*), получим следующую структуру оптимального портфеля:

Q^*= .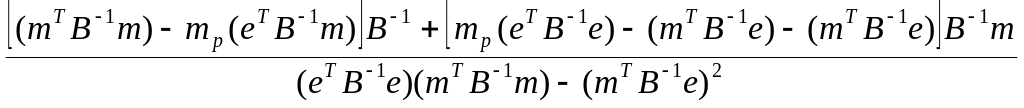

Можем найти наиминимальную дисперсию:

(σ_p^*)²=Q^*TBQ^*=

Если эффективности не коррелированны, то ковариационная матрица

диагональная

B=

Поэтому обратная к ней матрица тоже диагональна

B^-1=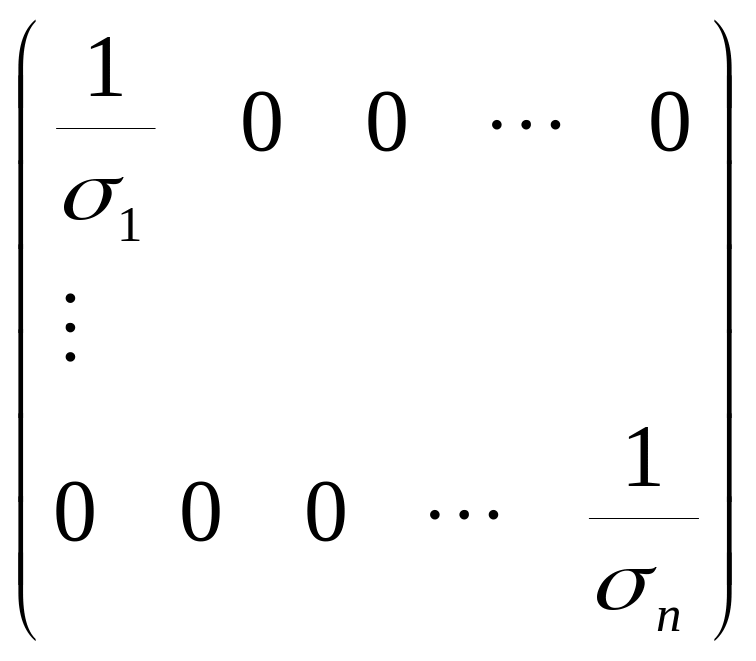

В таком случае выражение для оптимальной структуры и соответствующей ей дисперсии существенно упрощается. Вычислим некоторые составляющие, часто встречающиеся в этих выражениях:

e^TBe=

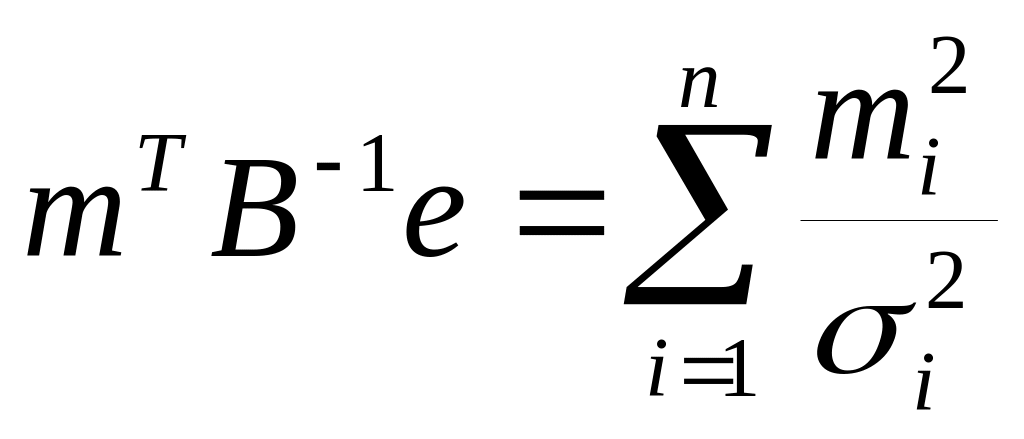
Назовем следующие естественные предположения:

1. Все эффективности ценных бумаг различны, т. е. из двух ценных бумаг с одинаковой эффективностью инвестор выберет бумагу с наименьшей дисперсией, в соответствие с этим проранжируем ценные бумаги в порядке убывания их средней эффективности: т₁>m₂>…>m_n.

2. Более высоким средним эффективностям соответствует большая дисперсия, это также естественно, так как из двух ценных бумаг одна из  имеет большую дисперсию и инвестор выберет всегда первую. Докажем, что в знаменателе выражений оптимального портфеля и соответствующей ему дисперсии стоит положительное число

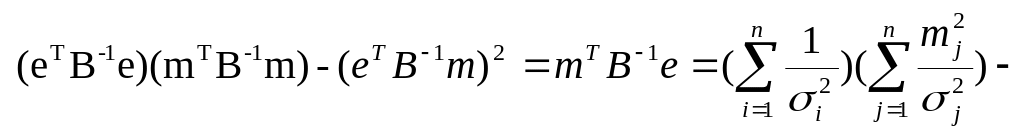
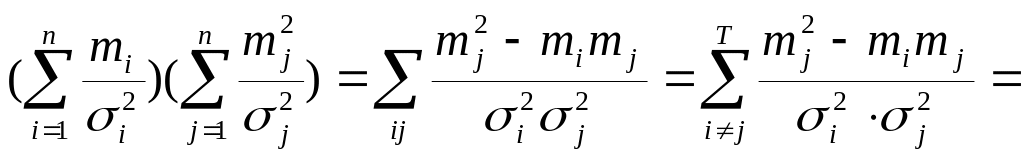
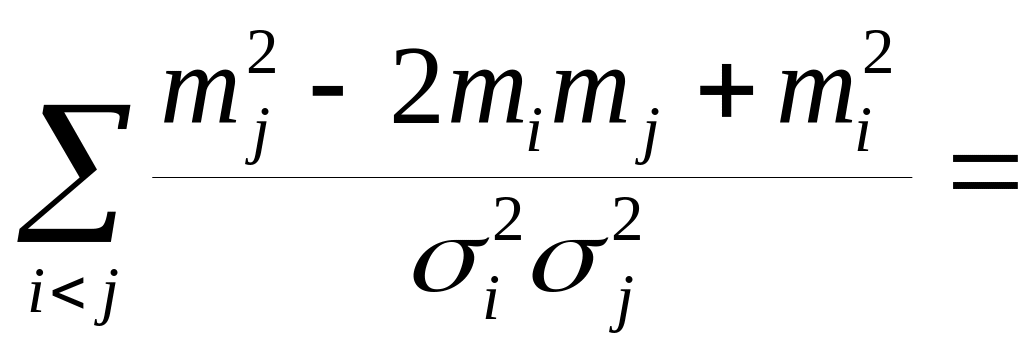. Аналогично докажем положительный знак числителя:

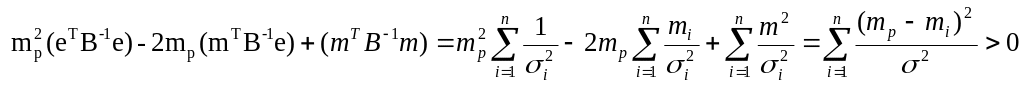
Дисперсия оптимального портфеля

(σ_p^*)²=Q^*TBQ^*= .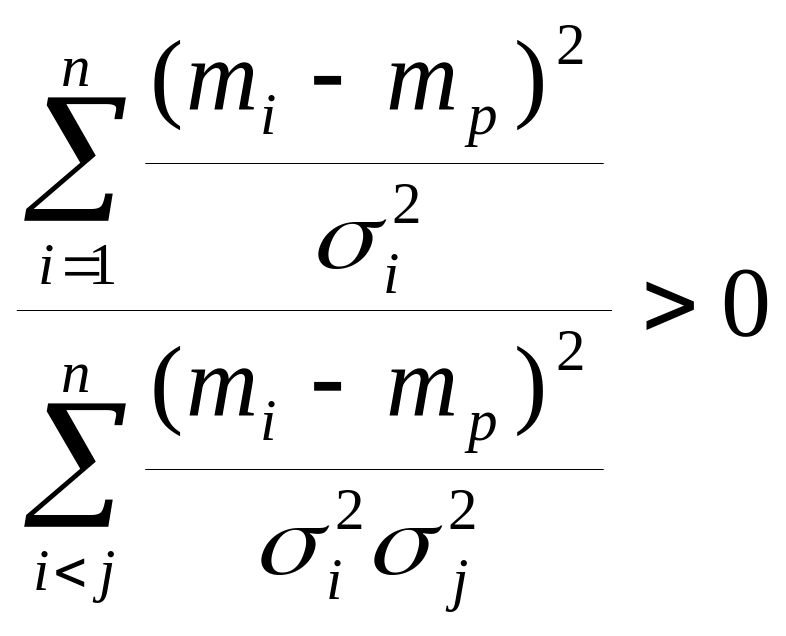

При отсутствии корреляции между эффективностями:

B^-1e= ; B^-1m=

Исходя из этого, выражение для оптимального портфеля принимает вид:

,

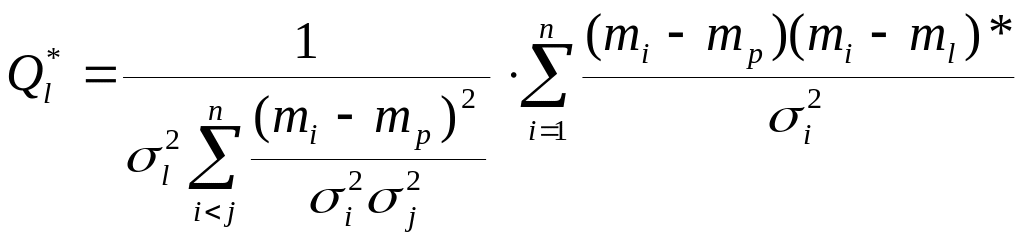l=1,…n.

Анализируя приведенное выражение, видно, что оно может содержать отрицательные элементы. В таком случае следует проводить перерасчет, последовательно исключая из портфеля наибольшие по модулю отрицательные компоненты.

m_p – математическое ожидание портфеля.

Задача

Инвестор может составить портфель из трех видов ценных бумаг: эффективности  R₁, R₂, R₃, причем эти эффективности являются некоррелируемыми случайными величинами, имеющими следующие m_x,

MR₁=11 ₁ =4

MR₂=10 ₂ =3

MR₃= 9 ₃ =1

MR_P=10

Необходимо найти такое соотношение Q₁, Q₂, Q₃ для любого из >0 и сумма Q_n=1, при 

MR_p= .

И при этом иметь min d_x

.

Имеем систему уравнений

Отбросим условие не отрицательности элементов. Для данной системы уравнений можно составить уравнение Лагранжа: