
- •Лабораторная работа № 3.20 Изучение модульного учебного комплекса мук-эм1.
- •Лабораторная работа № 3.21 Моделирование электростатического поля
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 4.21 Изучение работы источника напряжения
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Лабораторная работа № 4.24к Измерение сопротивления мостом постоянного тока
- •Краткие теоретические сведения
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 4.27 Исследование процессов заряда и разряда конденсатора и определение емкости конденсатора
- •Часть 2. Определение емкости конденсатора по измерению постоянной времени заряда или разряда и определение емкости системы конденсаторов.
- •Контрольные вопросы
- •Лабораторная работа № 5.21 Определение индуктивности соленоида и коэффициента взаимной индуктивности с помощью исследования вынужденных колебаний в rl – цепи.
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 5.27к Явление взаимной индукции
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 5.28к Магнитное поле на оси короткого соленоида
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 5.29к Моделирование работы конденсатора в электрической цепи
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 5.30 явление самоиндукции
- •Краткие теоретические сведения
- •Порядок выполнения работы
- •Порядок выполнения работы
- •Контрольные вопросы
- •Лабораторная работа № 6.22 Свободные (затухающие) колебания в последовательном rlc-контуре.
- •Порядок выполнения работы
- •Лабораторная работа № 6.24 Изучение сложениЯ колебаний
- •Порядок выполнения работы
- •Часть1. Определение разности фаз сонаправленных колебаний.
- •Часть2. Определение частоты неизвестных колебаний исследованием биений.
- •Часть3. Определение частоты неизвестных колебаний исследованием фигур Лиссажу.
- •Контрольные вопросы
- •Библиографический список
Порядок выполнения работы
1. Открыть диалоговое окно.
2. Произвести измерение сопротивления RX1 одного из резисторов. Для этого подобрать сопротивление RМ магазином сопротивления такое, чтобы сила тока, текущего через нуль-гальванометр, была минимальной.
3. Записать значение сопротивления RМ в таблицу и рассчитать RX1.
4. Проделать пункты 2 и 3 для двух других резисторов RX2, RX3.
5. Проделать пункты 2 и 3 для последовательного и параллельного соединения резисторов.
6. Рассчитать погрешности измерения сопротивления резисторов, считая, что относительная погрешность измерения сопротивлений R1 и R2 составляет 3 %, а RМ – 1 %.
Таблица 1
-
RМ, Ом
RХ, Ом
RХ, Ом
, %
RX1
RX2
RX3
Послед-ое
Паралл-ое
Контрольные вопросы
1. Что такое удельное сопротивление проводников?
2. Как зависит сопротивление проводников от температуры? В чем заключается явление сверхпроводимости?
3. Параллельное и последовательное сопротивление проводников.
4. Правила Кирхгофа и их применение к расчету сложных электрических цепей.
5. Какова суть метода моста постоянного тока для определения сопротивления резисторов?
Лабораторная работа № 4.27 Исследование процессов заряда и разряда конденсатора и определение емкости конденсатора
Ц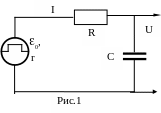 ель
работы: изучение временной зависимости
напряжения на конденсаторе при
подключении или отключении источника
постоянной ЭДС и определение емкости
конденсатора.
ель
работы: изучение временной зависимости
напряжения на конденсаторе при
подключении или отключении источника
постоянной ЭДС и определение емкости
конденсатора.
Приборы и принадлежности: генератор прямоугольных импульсов, электронный осциллограф, лабораторный стенд с набором конденсаторов и сопротивлений.
Краткие теоретические сведения
Рассмотрим процессы заряда и разряда конденсатора при подключении или отключении источника постоянной ЭДС о в схеме, представленной на рис.1. Включение и отключение ЭДС имитирует генератор прямоугольных импульсов напряжения. При включении ЭДС (появлении импульса) ток заряда конденсатора протекает по внутреннему сопротивлению источника и по сопротивлению R. Электрические заряды на обкладках конденсатора препятствуют прохождению электрического тока и уменьшают его. Пусть I, Q, U- мгновенные значения силы тока, заряда и напряжения на обкладках конденсатора. Уравнения, связывающие эти величины, имеют вид:
I
=![]() ,
(R+r)I = o-U,
Q = CU. (1)
,
(R+r)I = o-U,
Q = CU. (1)
Исключая в (1) I и U придем к уравнению
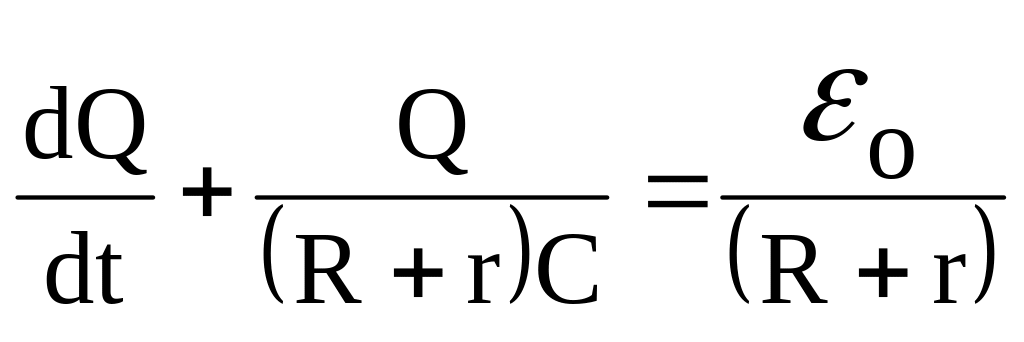 . (2)
. (2)
При решении уравнения учтем начальное условие: Q(0)=0. Это дает решение
![]() ,
(3)
,
(3)
где = (R+r)C - постоянная времени цепи заряда конденсатора. Выражение для U получим из связи между зарядом конденсатора и напряжением на его обкладках (рис.2)
![]() .
(4)
.
(4)
Прологарифмируем (4)
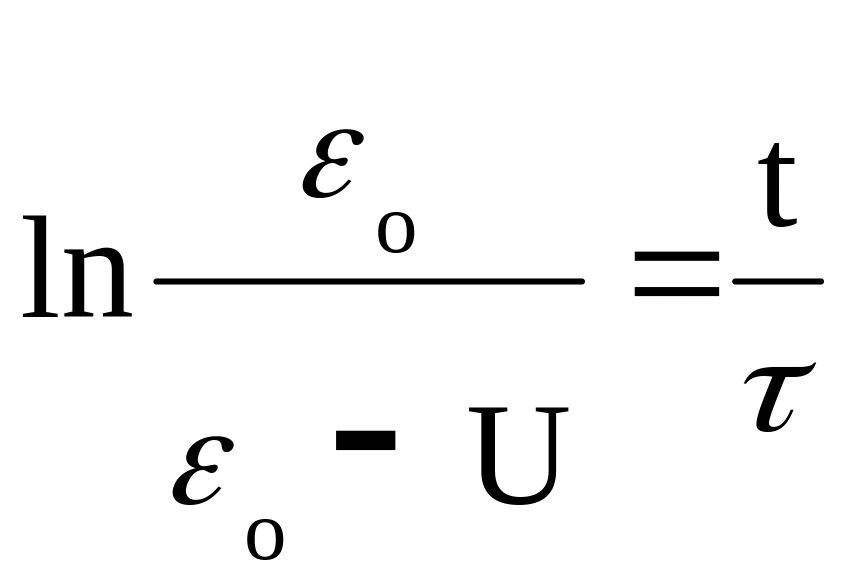
 .
(5)
.
(5)
И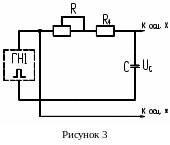 з
(5) следует, что ln(o/(o-U))
является линейной функцией времени и
по наклону прямой можно определить
постоянную времени цепи заряда
конденсатора .
Зависимость от
сопротивления R также линейная
= (R+r)C и позволяет определить величину
емкости конденсатора С и внутреннего
сопротивления источника ЭДС - r. Величину
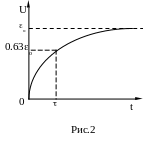
можно определить
из (5) как промежуток времени по истечении
которого напряжение на конденсаторе
достигает величины 0.63о.
з
(5) следует, что ln(o/(o-U))
является линейной функцией времени и
по наклону прямой можно определить
постоянную времени цепи заряда
конденсатора .
Зависимость от
сопротивления R также линейная
= (R+r)C и позволяет определить величину
емкости конденсатора С и внутреннего
сопротивления источника ЭДС - r. Величину
можно определить
из (5) как промежуток времени по истечении
которого напряжение на конденсаторе
достигает величины 0.63о.
При отключении ЭДС (окончании прямоугольного импульса) ток разряда конденсатора также протекает по сопротивлениям r и R. Для получения закона изменения напряжения на конденсаторе при его разряде достаточно в уравнении (2) положить 0 = 0 и принять начальное условие Q(0) = 0C. В результате получим
![]() .
(6)
.
(6)
Тогда
![]() (7)
(7)
Из (7) следует, что зависимость ln(Uc/0) от времени, как и в (5), линейная и может быть использована для определения емкости конденсатора.
Описание лабораторной установки.
Генератором прямоугольных импульсов является генератор напряжений ГН1 (выход «меандра»). На лабораторном стенде используются: переменный резистор R, постоянный резистор R4 и конденсаторы С1, С2 и С3. При использовании цифрового осциллографа ОЦЛ используется канал I.
Порядок выполнения работы.
Ч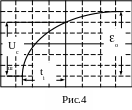 асть
1. Проверка закона заряда или разряда
конденсатора
асть
1. Проверка закона заряда или разряда
конденсатора
Собрать схему по рис. 3. Установить значение сопротивления R (по заданию преподавателя) в пределах 500-1500 Ом.
Подключить по указанию преподавателя один из конденсаторов С1, С2 или С3.
Установить частоту генератора 2500 Гц с помощью кнопки «F» на ГН.
И
 зменяя
коэффициент усиления (кнопки «Кус»
и «+» или «-») на осциллографе установить
размер изображения по вертикали в
пределах 4-7 делений шкалы согласно
примеру изображенному на рис.4.
зменяя
коэффициент усиления (кнопки «Кус»
и «+» или «-») на осциллографе установить
размер изображения по вертикали в
пределах 4-7 делений шкалы согласно
примеру изображенному на рис.4.Изменяя длительность развертки (кнопки «длит.» и «+» или «-») установить размер изображения заряда или разряда конденсатора по горизонтали в пределах 6-8 делений шкалы.
Если изображение не останавливается, можно воспользоваться кнопкой «стоп» и перемещать изображение с помощью кнопок «» и «,».
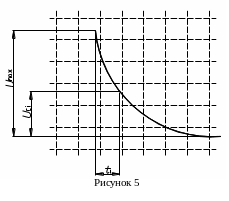
По экрану осциллографа измерить 6-8 пар значений (Uci - ti) (см. рис.4,5). Полученные результаты занести в таблицу 1.
Для заряда конденсатора построить график зависимости
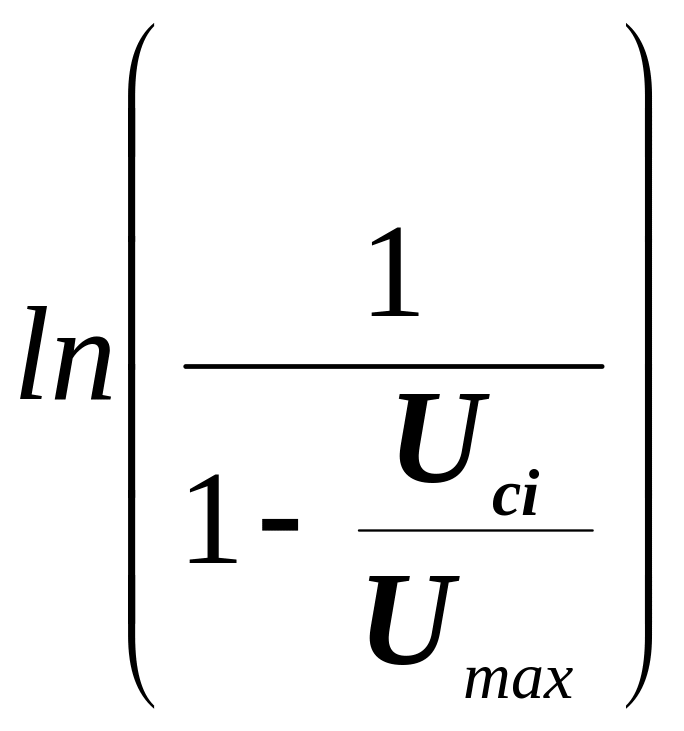 от времени t, для разряда конденсатора
график зависимости
от времени t, для разряда конденсатора
график зависимости
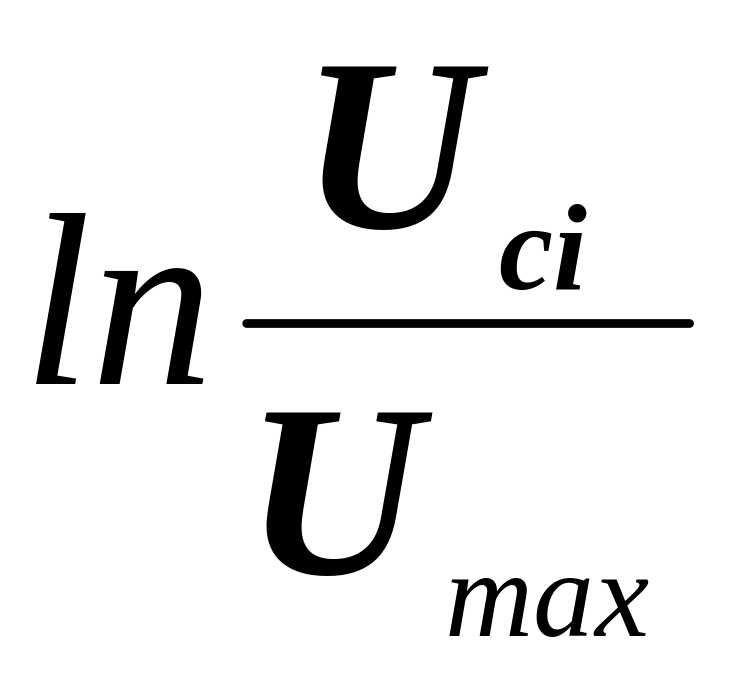 от времени t. Убедиться, что зависимость
носит линейный характер.
от времени t. Убедиться, что зависимость
носит линейный характер.П
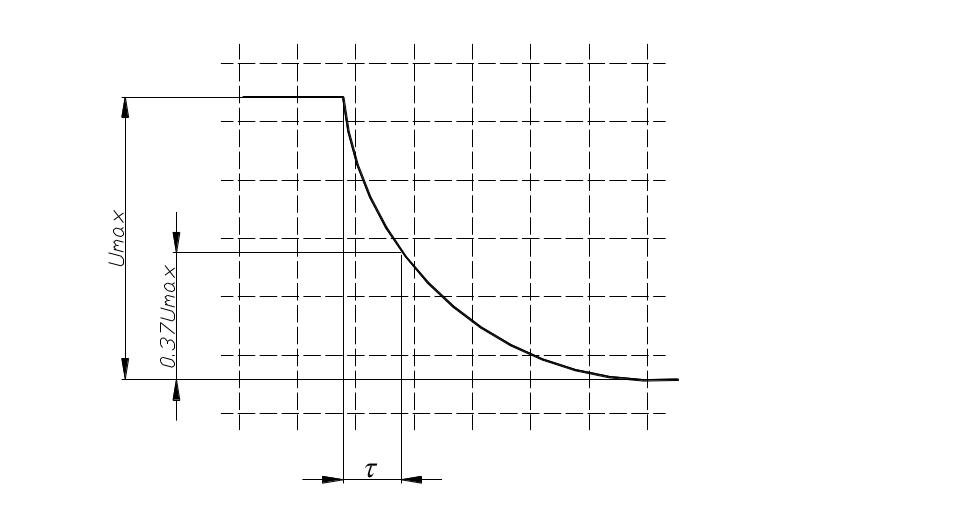 о
наклону прямой определить постоянную
времени которая
равняется тангенсу наклона прямой и
величину емкости С=/(R4
+ R). Результаты занести в табл.1.
о
наклону прямой определить постоянную
времени которая
равняется тангенсу наклона прямой и
величину емкости С=/(R4
+ R). Результаты занести в табл.1.
