Контрольные вопросы

1. Дифференциальное уравнение колебаний в последовательном RLC –контуре.

2. График затухающих колебаний. Коэффициент затухания, частота и период колебаний.

3. Логарифмический декремент затухания, добротность контура

4. Определение индуктивности контура в работе.

5. Определение логарифмического декремента затухания. Критическое сопротивление и его определение в работе.

Лабораторная работа № 6.22 Свободные (затухающие) колебания в последовательном rlc-контуре.

Цель работы: наблюдение затухающих колебаний на экране осциллографа и экспериментальное определение характеристик колебаний и параметров контура.

Приборы и принадлежности: генератор прямоугольных импульсов (в блоке ГН1), осциллограф ОЦЛ2, стенд С-ЭМ01, соединительные провода.

Краткие теоретические сведения

У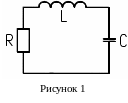 равнение свободных колебаний в последовательном RLC –контуре (рис.1) может быть получено из второго правила Кирхгофа:

U_c +U_R = _s,

где

Окончательно уравнение принимает вид

, (1)

где

Решением уравнения (1) при малом затухании (²_о²) является функция типа (рис.2)

(2)

где -частота затухающих колебаний, -коэффициент затухания.

Период затухающих колебаний при малом затухании можно приближенно считать равным периоду незатухающих колебаний

. (3)

Важной характеристикой затухающих колебаний является логарифмический декремент затухания, характеризующий уменьшение амплитуды колебаний за один период

, (4)

г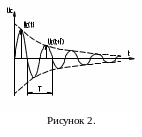 де U_c(t)-амплитуда затухающих колебаний в момент времени t; U_c(t+T)- амплитуда затухающих колебаний в момент времени t+T.

При малом затухании _о для  можно использовать формулу

, (5)

где R_конт- общее активное сопротивление контура.

где R – внешнее напряжение, r – внутренне сопротивление источника тока, активное сопротивление катушки.

Критическое сопротивление контура, при котором колебательный процесс переходит в апериодический, может быть найдено из условия _кр=_о.

. (6)

Добротность контура Q равна

. (7)

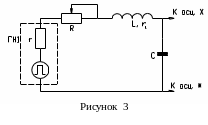
Порядок выполнения работы

1. Соберите схему, приведенную на рис.3. По указанию преподавателя подключите нужный вариант индуктивности (L₁, L₂). Включите внутреннее сопротивление ГН1 (кнопка «R_вн»). Установите частоту 1200 Гц.

2. Регулируя длительность развертки осциллографа («длит» и «+/-»), амплитуду импульса и коэффициент усиления осциллографа («К_ус» и «+/-»), добейтесь изображения 2-3 периодов колебания с амплитудой U_макс.= 6-8 клеток шкалы осциллографа.

3. Зная время развертки осциллографа, определите период затухающих колебаний для трех различных значений емкости С₁, С₂, С₃ при нулевом сопротивлении R. Для одной из емкостей (по указанию преподавателя) определите U_c(t) и U_c(t+T). Полученные результаты занести в таблицу 1.

4. Используя формулы (3), (4), (7) рассчитайте индуктивность контура, логарифмический декремент затухания и добротность при R=0 в этом случае 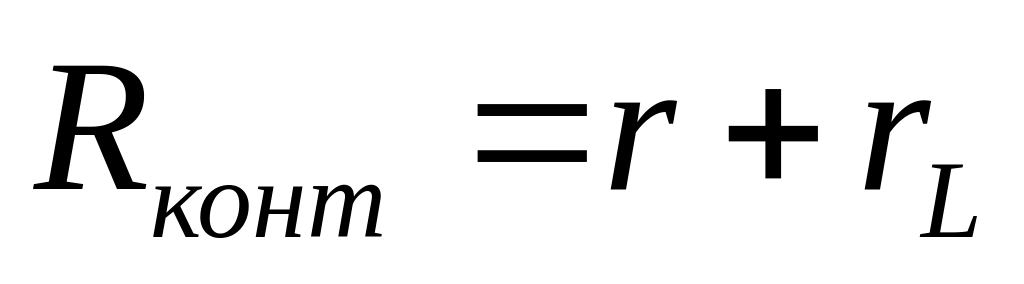. Результаты занесите в таблицу 1. Рассчитайте абсолютную L и относительную погрешности .

5. По формуле (5) зная , L, С и R=0 рассчитайте R_конт. По формуле R_конт=R+(r+r_L) определите (r+r_L). Результат занести в таблицу 2.

6. Наблюдая сигнал на осциллографе, доведите величину переменного сопротивления R до значения, при котором периодический процесс переходит в апериодический. При этом должны исчезнуть периодические колебания. Полученное значение R_к занесите в таблицу 2.

7. Складывая полученное значение R_к с найденным в п.5 сопротивлением (r+r_L), получите опытное значение R_крит=R_к+(r+r_L) Занесите результат в таблицу 2.

8. Сравните полученное в опыте значение R_крит. с теоретическим значением, которое находится по формуле (6).

Таблица 1

№	Сi,мкФ	Тi, мкс	Uc(t), дел.	Uc(t+T), дел.	 ,	Q	Li, мГн	<L>, мГн	L, мГн	, %
1
2
3

Таблица 2

С, мкФ	<L>, мГн		(r+rL), Ом	Rк, Ом	Rкрит., Ом	Rкр. теор., Ом

Контрольные вопросы

1. Дифференциальное уравнение колебаний в последовательном RLC –контуре.

2. График затухающих колебаний. Коэффициент затухания, частота и период колебаний.

3. Логарифмический декремент затухания, добротность контура

4. Определение индуктивности контура в работе.

5. Определение логарифмического декремента затухания.

Лабораторная работа № 6.21к

Изучение явления резонанса в последовательном колебательном контуре.

Цель работы: изучить зависимость напряжения на конденсаторе последовательного колебательного контура от частоты вынуждающей ЭДС; определить по результатам измерений параметры колебательного контура.

Работа выполняется на ЭВМ

Краткие теоретические сведения

Последовательный колебательный контур состоит из конденсатора емкостью С, катушки индуктивностью L, омического сопротивления R и источника переменной ЭДС , включенных между собой последовательно (рис.1).

В ынуждающая гармоническая ЭДС изменяется по закону  = _оSint, где  - частота переменной ЭДС. Составим дифференциальное уравнение, описывающее колебательный процесс в рассматриваемом контуре, использя второе правило Кирхгофа.

IR + U_c =  +_s , (1)

где U_c- напряжение на емкости, _s- ЭДС самоиндукции, возникающая в катушке индуктивности. Силу тока в цепи и напряжение на конденсаторе можно связать, рассматривая процесс изменения заряда конденсатора.

. (2)

Подставляя (2) в (1), получим

. (3)

Введем обозначения: R/2L=, 1/LC=_o² и _o/LC=E_o (_о- частота собственных колебаний контура, - коэффициент затухания). После подстановки в (3) получим неоднородное дифференциальное уравнение вынужденных колебаний

, (4)

решением которого является сумма частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения, которым в установившемся режиме можно пренебречь. Частное решение уравнения (4) имеет вид:

U_c = U_c()sin(t +), (5)

где:

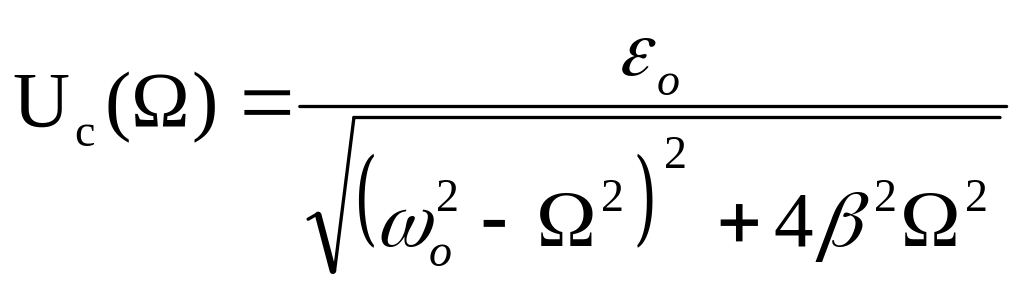, (6)

. (7)

Uc()-амплитуда вынужденных колебаний напряжения на емкости,

- сдвиг фаз колебаний напряжения на емкости по отношению к колебаниям вынуждающей ЭДС. Вынужденные колебания происходят с частотой вынуждающей ЭДС. Исследование зависимости Uc от  показывает:

1. при   0 напряжение на емкости U_c _о;

2. функция U_c=U_c() обладает максимумом U_c^max при частоте генератора _р = 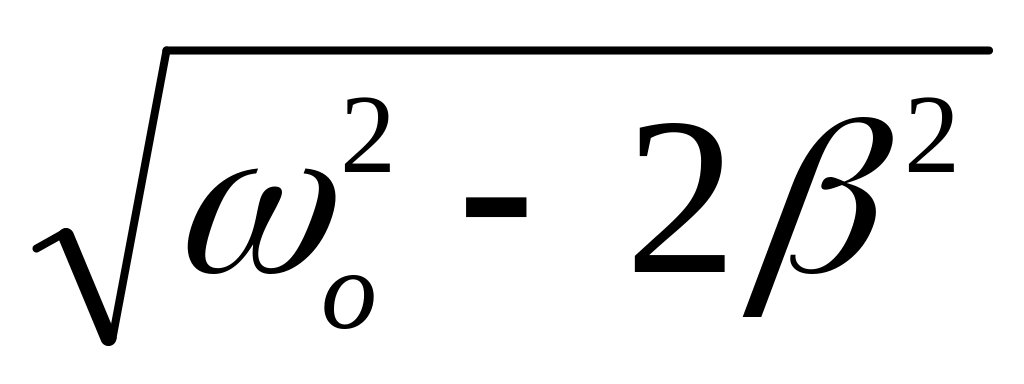(доказать самостоятельно);

3. при    напряжение на емкости U_c 0.

Зависимость напряжения на емкости от частоты вынуждающей ЭДС носит название резонансной кривой. Положение максимума резонансной кривой зависит от коэффициента затухания (рис.2).

Д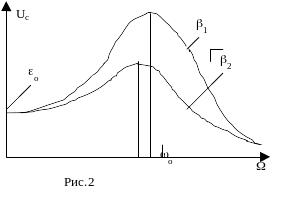 ля колебательного контура вводится понятие добротности, которая определяется как

Q = U_o^max/_o. (8)

Или

Q = , (9)

где R_к – сопротивление источника тока и активное сопротивление катушки. Зная несколько сопротивлений R_i, включаемых в контур, можно определить величину R_к:

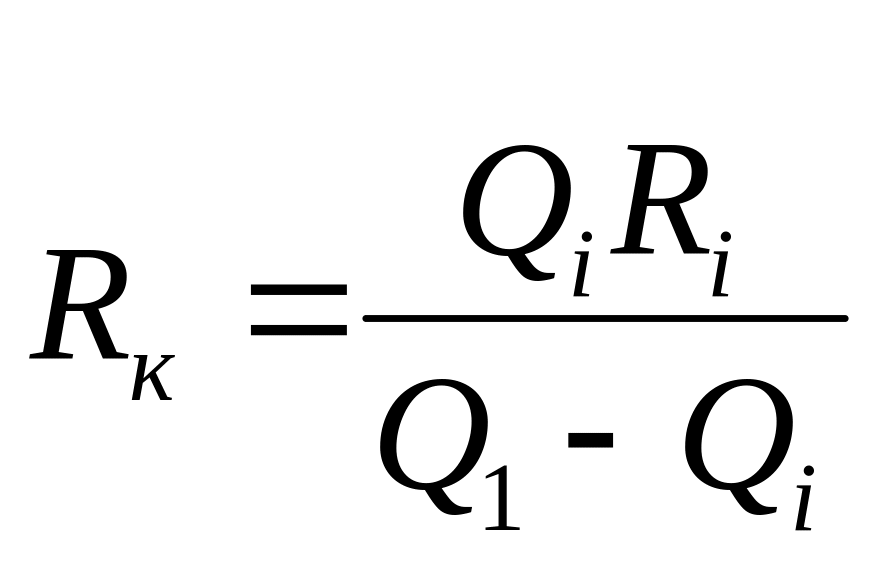. (10)

Если _о, резонансная частота _р_о и индуктивность контура может быть вычислена

L = 1/_o²C, _o_Ро=2_Ро. (11)

Зная величину индуктивности и сопротивление в контуре можно вычислить коэффициент затухания по соотношению

_i=(R_к + R_i)/2L. (12)

Порядок выполнения работы

1. Открыть диалоговое окно (щёлкнув дважды по «ярлык для резонанса» на рабочем столе), выбрать в меню «резонанс напряжения в RLC-контуре».

2. Установить значение емкости контура (по указанию преподавателя), занести значения С и _о в табл.1.

3. Получить изображения 4^х резонансных кривых, устанавливая значения R_м– 0, 100, 250, 500 Ом и активируя «мышкой» клавишу «строить».

4. Установить значение частот левой и правой границ в диапазоне примерно  10, 20 кГц от резонансной частоты, активируя режим масштабирования (кнопка с изображением увеличительного стекла). Занести значения U_c для 10 частот из диапазона масштабирования в табл.1.

5. Определить резонансные частоты _р, величины U_Cmax и занести в табл.1

6. Построить резонансные кривые U_c = U_c().

7. Вычислить величину добротности по формуле (8) и сопротивление контура R_к через добротности для различных сопротивлений R_м по (10). Результаты занести в табл.2

8. Вычислить индуктивность контура по резонансной частоте при Rм=0 и емкости конденсатора С (полагая  2o) по формуле (11).

9. Вычислить коэффициенты затухания _i по соотношению (12), записать результаты в табл.2 и сравнить со значениями резонансных частот _рез.

10. Сделать вывод о степени затухания колебаний в контуре.

Таблица 1.

	о=				С =
	Rм=0 Ом		Rм=100 Ом		Rм=250 Ом		Rм=500 Ом
	, кГц	Uc, В	, кГц	Uc, В	, кГц	Uc, В	, кГц	Uc, В
1
. . .
10
рез, кГц
Ucmax, В

Таблица 2.

Rм, Ом	Qi	RКi, Ом	Rк, Ом	DRк, Ом	, %	i	резi, с-1
0
100
250
500

Контрольные вопросы

1. Вынужденные колебания в контуре RLC-контуре, их возникновение, дифференциальное уравнение этих колебаний и его решение. Частота вынужденных колебаний.

2. Понятие электрического резонанса. Резонанс напряжения в контуре. Резонансная частота.

3. Добротность колебательного контура и определение добротности в данной работе.

4. Определение индуктивности контура в лабораторной работе. Определение сопротивления контура в лабораторной работе.

5. Определение контура коэффициента затухания в лабораторной работе.