Лабораторная работа № 5.30 явление самоиндукции

Цель работы: ознакомиться с явлением самоиндукции; изучить зависимость постоянной времени электрической цепи, состоящей из катушки индуктивности и омического сопротивления, от величины сопротивления; определить величины индуктивности катушки и магнитной проницаемости сердечника соленоида.

Приборы и принадлежности: генератор прямоугольных импульсов, электронный осциллограф, лабораторный стенд, магазин сопротивлений.

Краткие теоретические сведения

Явление самоиндукции заключается в возникновении ЭДС индукции в электрической цепи, обладающей индуктивностью, при изменении в ней электрического тока.

Электрический ток, протекая по проводникам, создаёт в окружающем пространстве магнитное поле. Магнитный поток этого поля, сцеплённый с контуром проводника  (потокосцепление самоиндукции), вычисляется по формуле

, (1)

где N – число витков соленоида.

Интегрирование в (1) ведётся по сечению соленоида.

При слабых магнитных полях и неизменных параметрах контура, как правило, потокосцепление пропорционально силе тока:

=LI. (2)

Коэффициент пропорциональности L называется индуктивностью контура. Индуктивность характеризует способность проводящего контура создавать потокосцепление собственного магнитного поля с контуром проводника. Она численно равна потокосцеплению при силе тока, равной единице:

L=I. (3)

Индуктивность измеряется в генри: 1Гн=Вб/А. Индуктивность - скалярная величина, не зависящая от протекающего по контуру тока (в отсутствии ферромагнитных сред).

Согласно закону электромагнитной индукции, возникающая в цепи ЭДС самоиндукции равна скорости изменения потокосцепления самоиндукции:

_s= - ddt. (4)

Если L - величина постоянная, то из (2) получаем

_i = - L dI/dt. (5)

Знак минус отражает тот факт, что в проводящем контуре ЭДС самоиндукции всегда препятствует изменению электрического тока, т.е. стремится поддерживать силу тока неизменной. Самоиндукция в электромагнетизме играет ту же роль, что и инерция в механике.

Используя выражения (1) и (3), можно получить формулу для индуктивности соленойда, выбрав поверхность интегрирования, перпендикулярную осевой линии соленойда.

L=_N²Sl (6)

где ₀=4 10^-7Гн/м - магнитная проницаемость сердечника соленойда, N - общее число витков, S - площадь поперечного сечения, l- длина соленойда.

Рассмотрим переходные процессы в индуктивно-резистивной цепи, которая состоит из омического сопротивления R, индуктивности L и источника ЭДС (рис.1).

По закону Ома для замкнутой цепи

=(+_s)/R, (7)

учитывая (5), получим дифференциальное уравнение первого порядка

I R= - LdI/dt. (8)

Д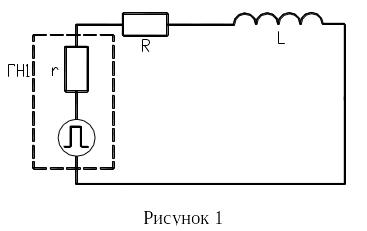 ля его решения (8) введём начальные условия: пусть при t=0, =0 и I=0; при t>0, =const и II(t). Найдём функциональную зависимость силы тока от времени. Для этого в (8) разделим переменные и проинтегрируем обе части уравнения, расставив пределы интегрирования с учётом начальных условий.

(9)

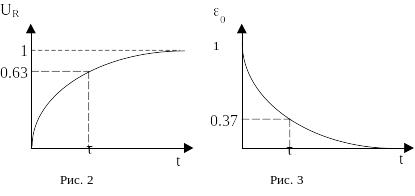П осле интегрирования

I/R)[1 - exp(-Rt/L)]. (10)

Согласно (10) и закону Ома для участка цепи, напряжение на активном сопротивлении R U=IR=[1-exp(-Rt/L)], (11)

а на индуктивности L

_s=- exp(-Rt/L)=- exp(-t/). (12)

Величину =L/R называют постоянной времени цепи, которая равняется времени, за которое интенсивность уменьшается в e раз, т.е. U=0.37 U_max , а при зарядке конденсатора =0,63U_max. Она равна времени, за которое величина _s уменьшится в 2,7 раза, а напряжение на сопротивлении возрастёт до величины 0,63. Графики зависимости U и _s от времени показаны на рис. 2 и 3.

Поскольку реальные источники  обладают внутренним сопротивлением r, то постоянная времени

=L/(R+r) или 1/=R/L+r/L. (13)

Как видно из выражения (13), зависимость 1/ от R является линейной.