Контрольные вопросы

1. В чем заключается явление электромагнитной индукции? Сформулировать закон Фарадея для электромагнитной индукции.

2. Какова суть явлений взаимной индукции?

3. Дать понятие о потоке магнитной индукции и потокосцеплении.

4. Вывести формулу для ЭДС взаимной индукции для случая соосных контуров и гармонических колебаний.

Лабораторная работа № 5.28к Магнитное поле на оси короткого соленоида

Цель работы: ознакомиться с баллистическим методом измерения магнитной индукции магнитного поля соленоида.

Работа выполняется на ЭВМ.

Краткие теоретические сведения

Баллистический метод измерения магнитной индукции.

В основе баллистического метода измерения магнитной индукции лежит явление электромагнитной индукции (ЭМИ). Поместим в магнитное поле небольшую многовитковую катушку, в цепь которой включим баллистический гальванометр. Тогда при всяком изменении магнитного поля будет изменяться потокосцепление катушки и в цепи катушки появится индукционный ток. Величина заряда, прошедшего через гальванометр, пропорциональна изменению потокосцепления:

. (1)

Потокосцепление зависит от числа витков катушки и магнитного потока через ее поверхность:

. (2)

При неизвестном направлении магнитной индукции следует выбирать ориентацию катушки таким образом, чтобы изменение потокосцепления и, следовательно, показания гальванометра были максимальными.

Если направление индукции определено и размеры катушки достаточно малы, чтобы поле в пределах катушки можно было считать однородным, то выражение (2) переходит в (3):

, (3)

где, N-число витков катушки; S-площадь одного витка.

Изменение потокосцепления при выключении поля равно NBS, при изменении направления поля на противоположное – 2NBS.

Баллистический гальванометр – электроизмерительный прибор с большим периодом собственных колебаний подвижной рамки, предназначенный для измерения величины заряда, проходящего через него, при коротких импульсах электрического тока.

Если время изменения потокосцепления много меньше периода собственных колебаний рамки гальванометра, то заряд, прошедший по цепи, пропорционален показаниям баллистического гальванометра:

q = C_q, (4)

где, С_q- чувствительность баллистического гальванометра, Кл/дел; - показание гальванометра, дел.

При изменении направления магнитного поля на противоположное, объединяя (4), (3) и (1), получим выражение для магнитной индукции:

. (5)

Таким образом, помещая небольшую многовитковую катушку в различные точки магнитного поля, по показаниям баллистического гальванометра можно определить значение магнитной индукции в этих точках.

Магнитное поле на оси короткого соленоида.

В ыделим малый участок длины соленоида dx, по которому протекает ток силой dI (рис. 1), и воспользуемся выражением для магнитной индукции на оси кругового тока:

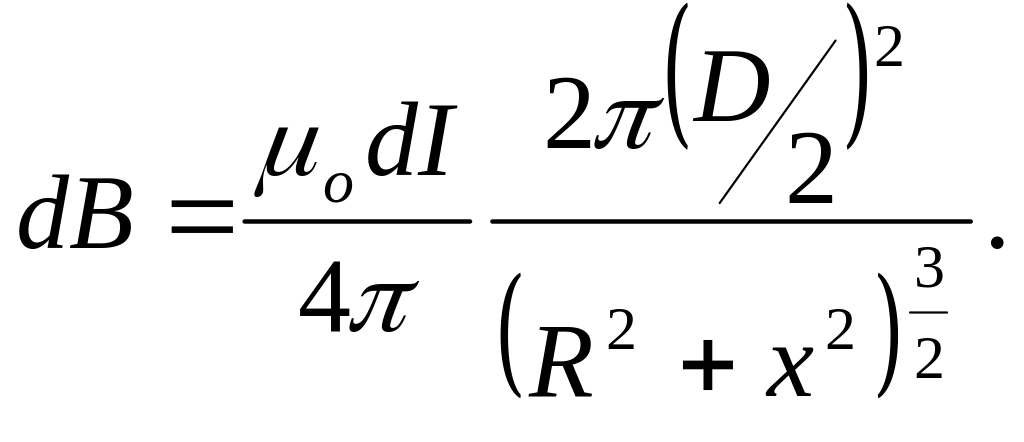(6)

Интегрируя (6) по х от 0 до L и переходя к углам ₁ и _2, получим выражение для магнитной индукции на оси соленоида:

, (7)

где, I- сила электрического тока, протекающего по соленоиду; n- плотность намотки (число витков на единицу длины соленоида).

,
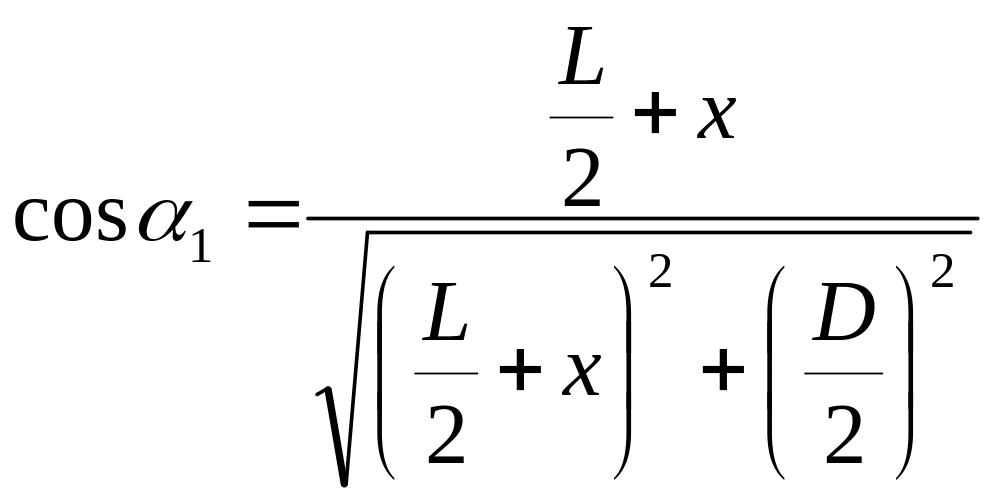