Лекция №12

Регулирование конденсационных турбоагрегатов

Простейшая схема конденсационного турбогенератора изображена на рис.1.

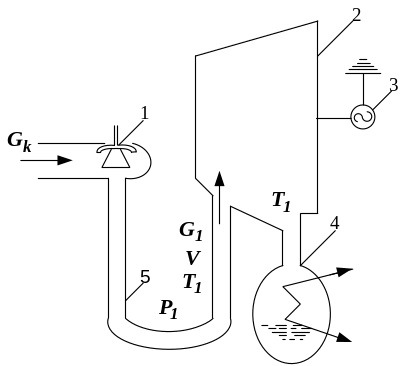
Рисунок 1 Схема конденсационной паровой турбины:

1– клапан; 2 – турбина; 3 – электрогенератор; 4 – конденсатор;

5 – паровой объём.

Пар в турбину 2 поступает через клапан 1. Между клапаном и лопаточным аппаратом расположен паровой объём 5. Пар из турбины поступает в конденсатор 4.

Пар к турбине подводится из паровых каналов, аккумулирующихся способность которых настолько велика, что они считаются в САР как источники неограниченного рабочего тела. В связи с этим температуру пара перед турбиной и его давление считают постоянными. При этом регулирование скорости паровых турбин осуществляется путём воздействия регулятора на распределительные органы рабочего тела – клапаны.

Перемещение клапана вызывает дросселирование пара, вследствие чего уменьшается количество и качество пара поступающего в турбину.

Для всех существующих способов регулирования (дроссельном, сопловом и обводном) переход от одного режима роботы к другому связан с изменением, как расхода, так и состояние пара, поступающего в турбину, то есть используется количественный и качественный принцип регулирования. Задачей регулирования конденсационных турбоагрегатов является поддержание в узких пределах их скорости вращения при коэффициенте неравномерности регулирования 2…4 %.

В качестве командующих органов применяются конические центробежные регуляторы, центробежные и зубчатые насосы в соединении с регуляторами давления масла. Широко применяется непрямое регулирование с одинарным, двойным и тройным усилением.

Вследствие высоких напряжений, возникающих во вращающихся деталях паровых турбин, жесткие требования проявляются в отношении ограничения разгона турбогенератора.

Для решения современных задач регулирования паровых турбин за это время всё более широко применяется различные корректирующие устройства: регулирование с дополнительными импульсами по производной и по нагрузке.

Уравнение парового объёма между клапаном и турбиной

Согласно принципу работы турбины и её схемы (рис.1) противодавление Р₂ очень мало по сравнению с давлением и температурой изменяется незначительно. Поэтому можно принять:

.

(1)

Расход пара через клапан подсчитан по формуле Бендемана

,

(2)

где – живое сечение клапана в м²;

, –начальное давление и удельный объем в кгс/м² и м³/кг;

– давление за клапаном в кгс/м²;

– коэффициент расхода, определяющийся опытным путем.

Разность между расходом пара клапаном и турбиной вызывает изменение удельного веса пара γ в рассматриваемом пространстве согласно уравнению

,

Расход зависит от величины подъема клапана, то есть от положения усилителя, определяемого координатой m, и от давления за клапаном (давление за клапаном полагают постоянным). Так как температуру за клапаном можно считать алгебраически связанной с давлением в паровом объеме , то расход является функцией только от . Поэтому для малых колебаний будут иметь силу уравнения:

,

(3)

.

(4)

Производные в (3) и (4) находятся путем дифференцирования (1) и (2)

.

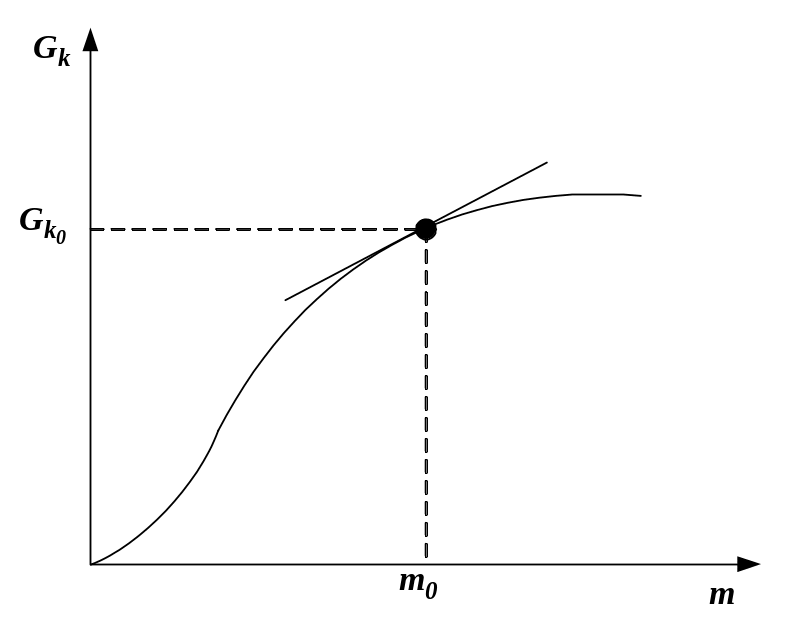
Рисунок 2 К вычислению частных производных

,

(5)

или графически (на основании характеристики клапанов)

При политропном состояния пара в паровом объёме ,

где – показатель политропа можно записать:

,

(6)

где ; ; ; ; .

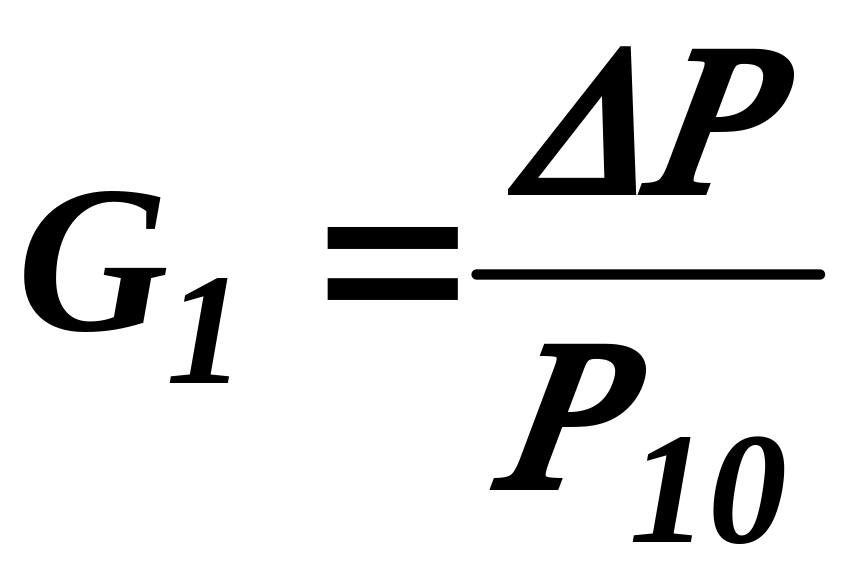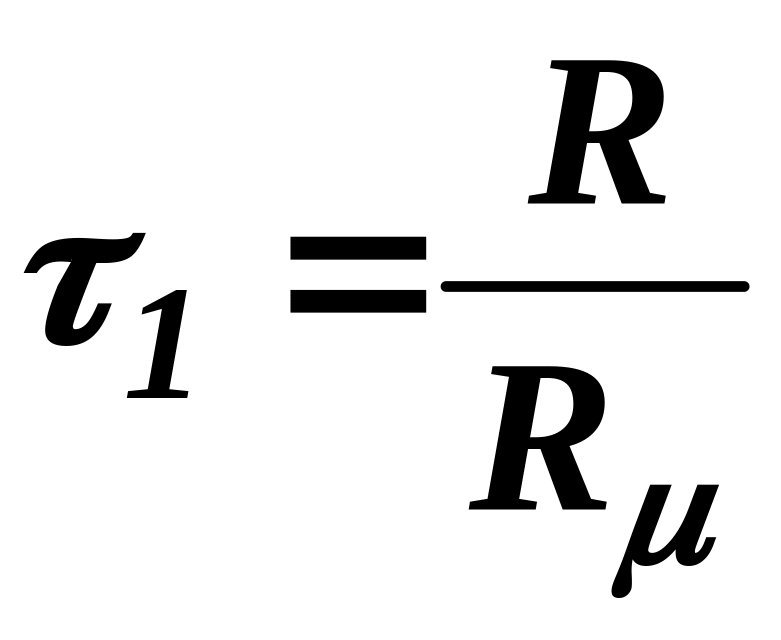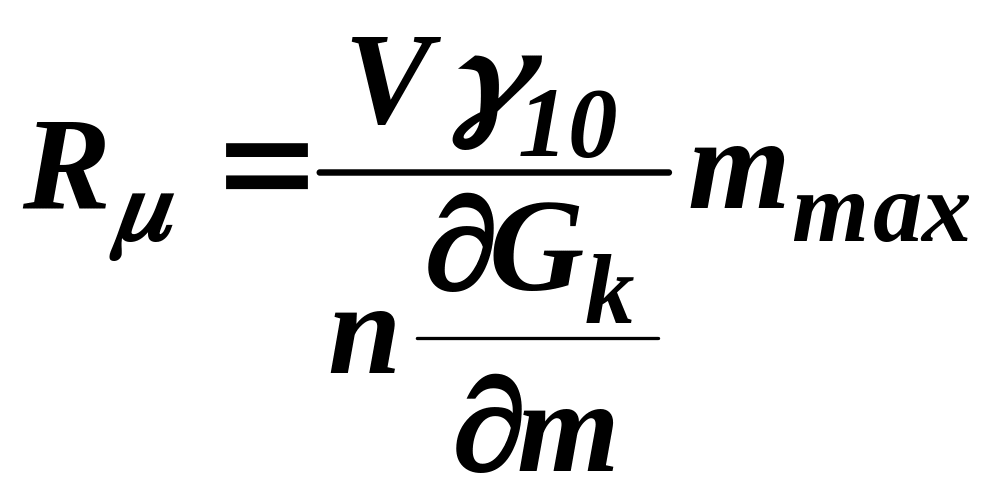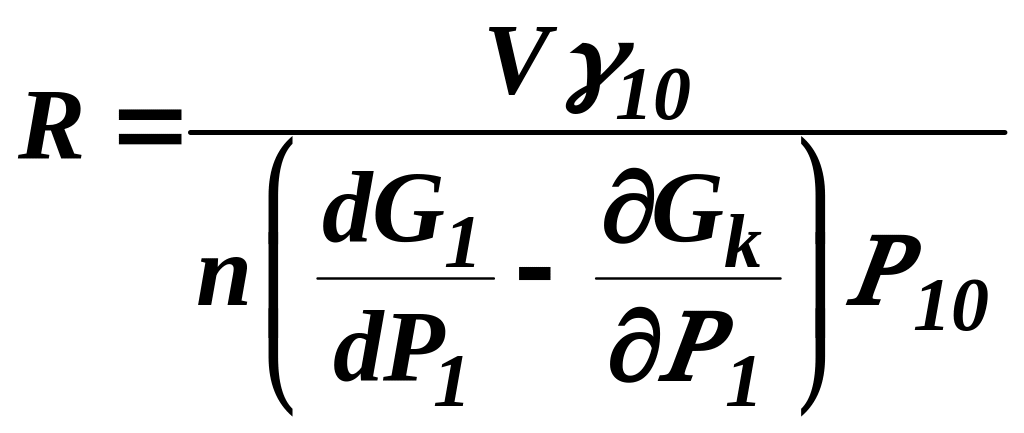После преобразования Лапласа уравнения парового объёма запишем:

,

(7)

или

.

Таким образом, паровой объём между клапаном и соплами в структурной схеме можно представить с перемещением звеном, передаточной функцией которого

.

(8)

Влияние парового объёма на процесс регулирования

Структурная схема конденсационной турбины как динамической системы (рис. 3)

Рисунок 3 Структурная схема регулирования турбины с паровым объёмом.

Здесь – колебательное звено (регулятор);

, , – апериодические звенья соответственно усилителя, парового объёма и турбины.

Рассмотрим систему регулирования при условии малого значении времени усилителя ТS. Такому процессу регулирования соответствуют прямое (пропорциональная по отклонению) регулирования, при исследовании которого воспользуются уравнением:

а) Уравнение идеального регулятора ;

б) Уравнение ротора .

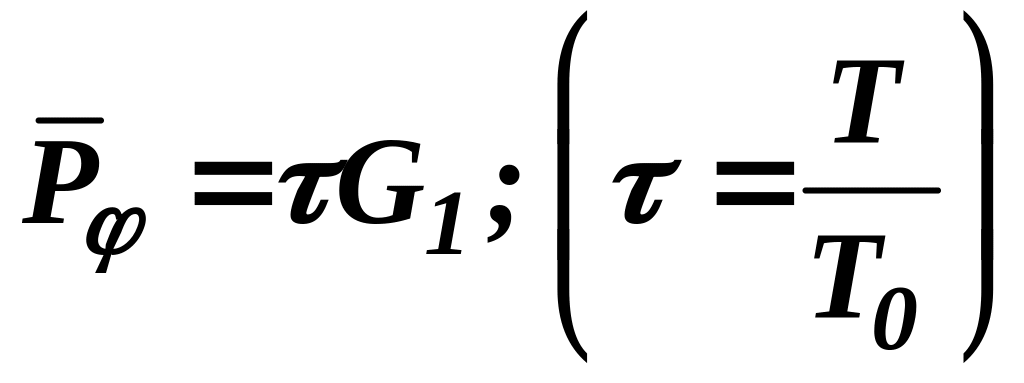Уравнение парового объёма ,

где ; .

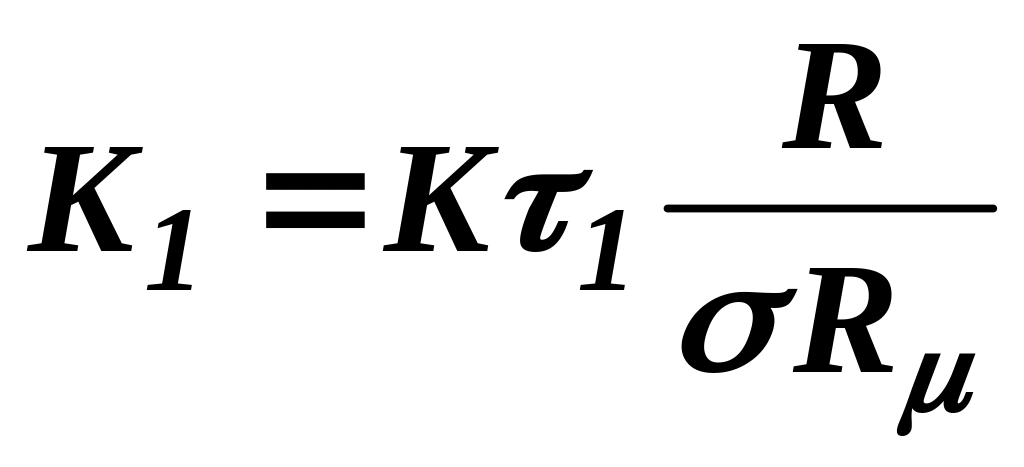При таких предположениях колебательное звено превращается в кинематические связи и остаётся лишь два апериодических звена (рис. 4)

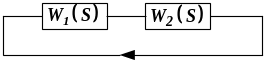
Рисунок 4 – Структурная схема

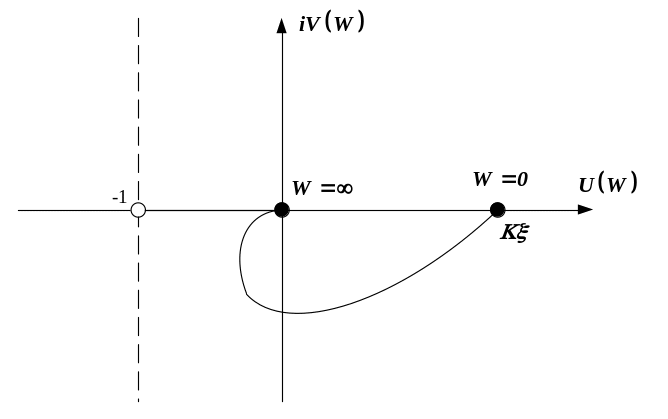
Рисунок 5 Амплитудно–фазовая передаточной функции разомкнутой системы

Подставив вместо , получим амплитудно–фазовую характеристику разомкнутой системы:

.

Так как мнимая часть всегда отрицательная, то характеристика находится в нижней части полуплоскости и точка (–1, ) не может оказаться охваченной этой кривой. Таким образом, такая система, состоящая из двух апериодических звеньев в замкнутом состоянии всегда устойчива.

, .

, .

.

, .

.

.

.

.
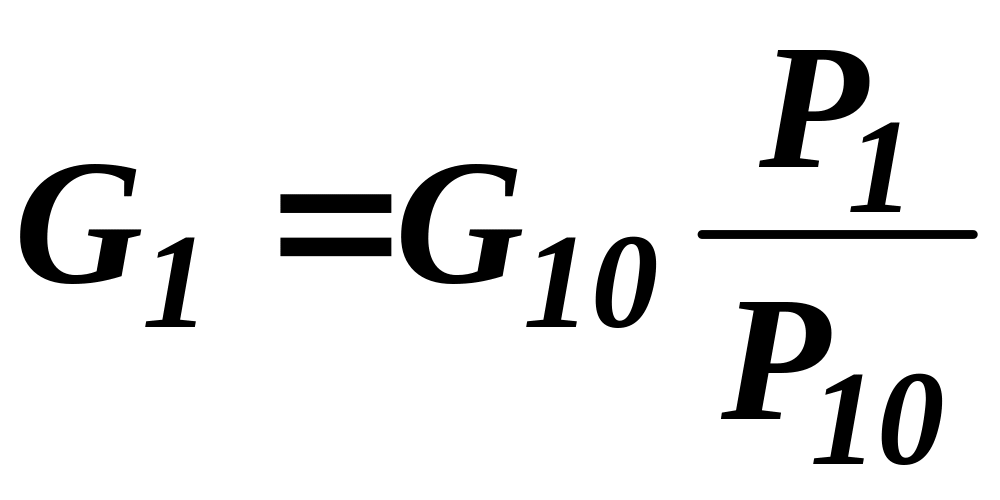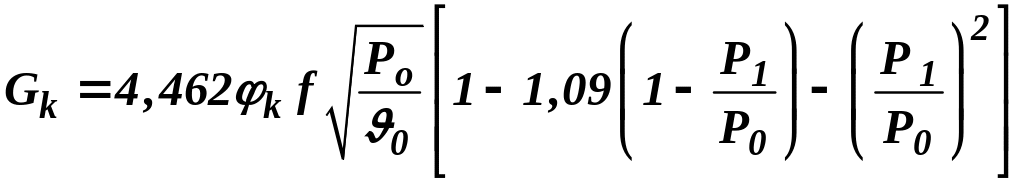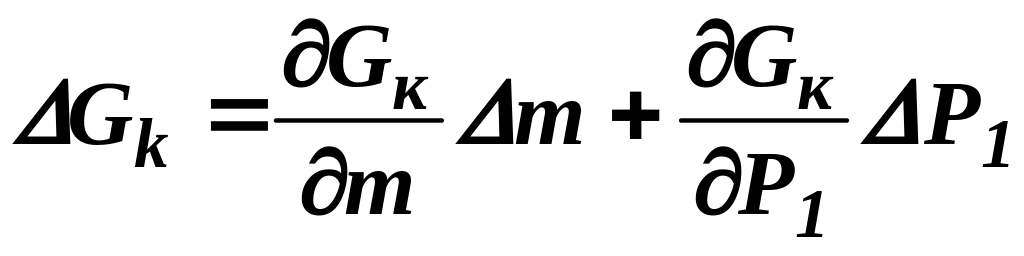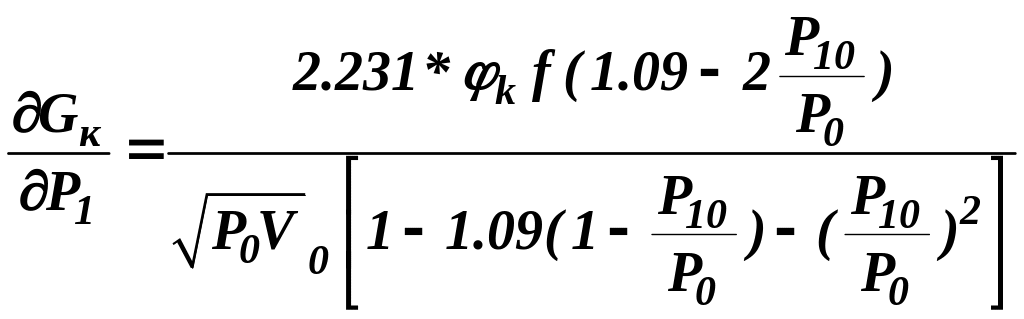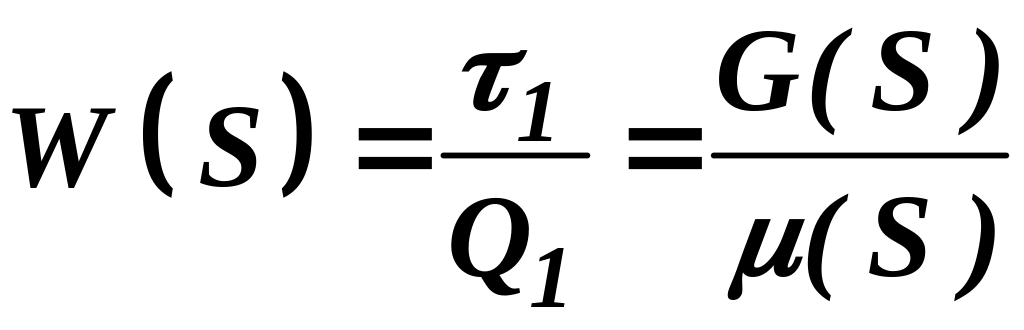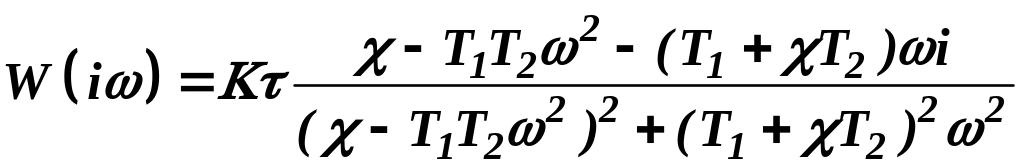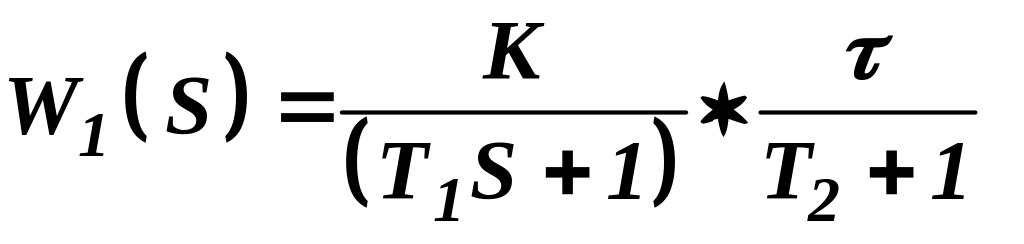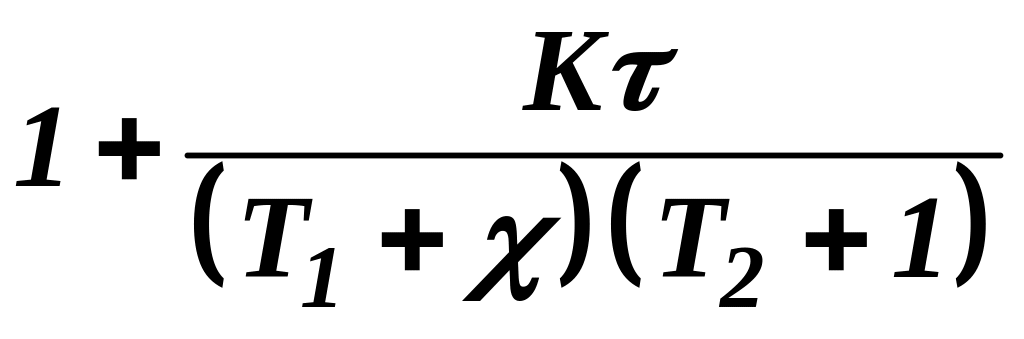