Лекция №11 Уравнение регулятора

Центробежный регулятор (центробежный маятник)

Рассмотрим силы, действующие на муфту регулятора скорости. К муфте приложены две приведенные силы:

1. упругая или поддерживающая сила ;

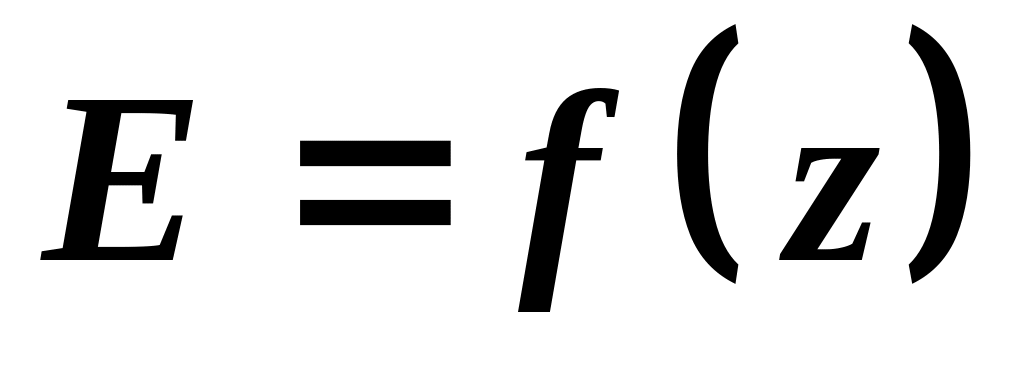2. регулирующая (приведенная центробежная)сила .

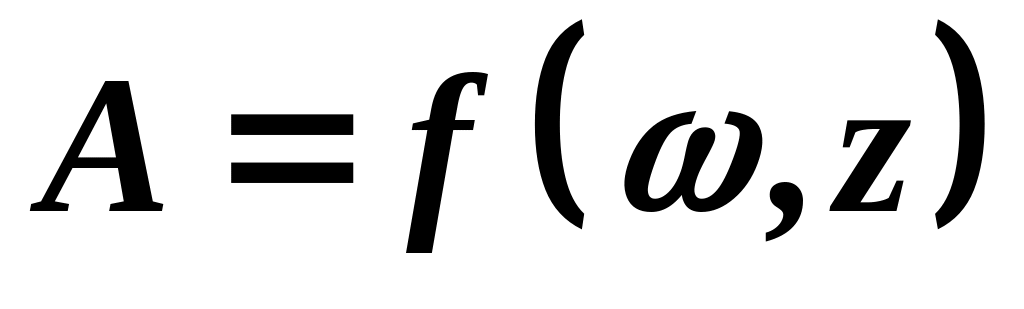Изобразим зависимости и .

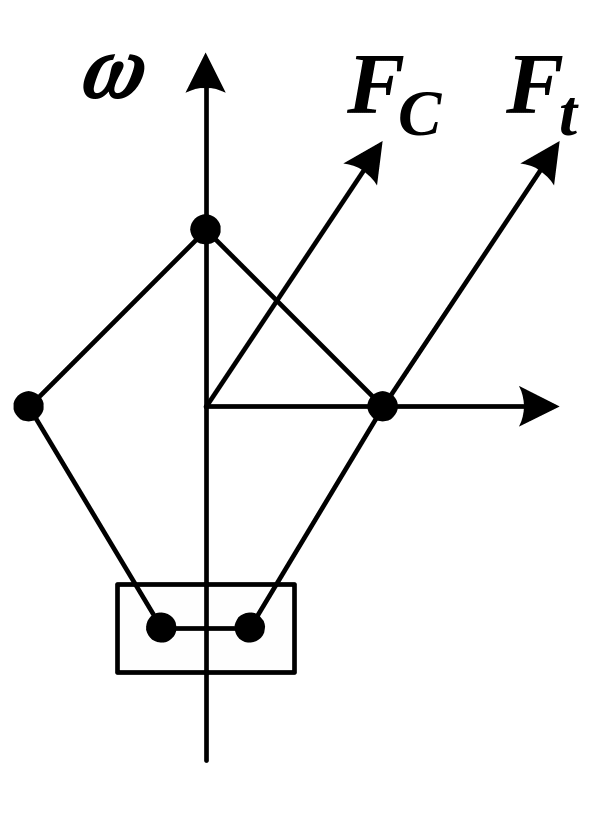
При установившемся движении, которому соответствует координата z₀ (точка А на рис. 1), регулятор находится в равновесии:

.

(1)

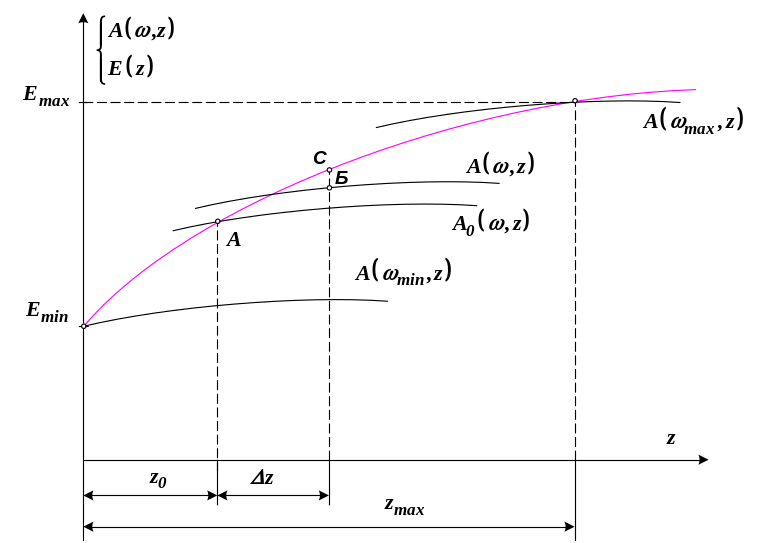
Рисунок 1 Силы действующие на муфту регулятора скорости

Предположим, мы имеем дело с малым возмущением силового поля, а следовательно, с малыми колебаниями муфты около положения равновесия:

Обозначим массу, приведенную к муфте, через М, тогда движение регулятора описывается дифференциальным уравнением

,

(2)

Далее обозначим:

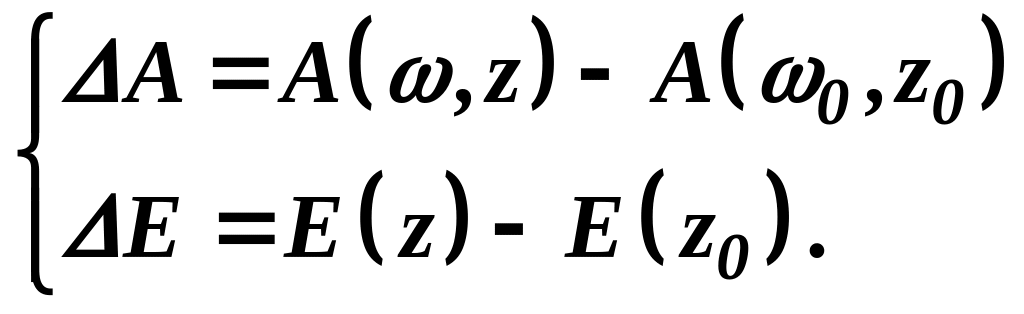
Вычтем (1) из (2), получим уравнение малых колебаний регулятора

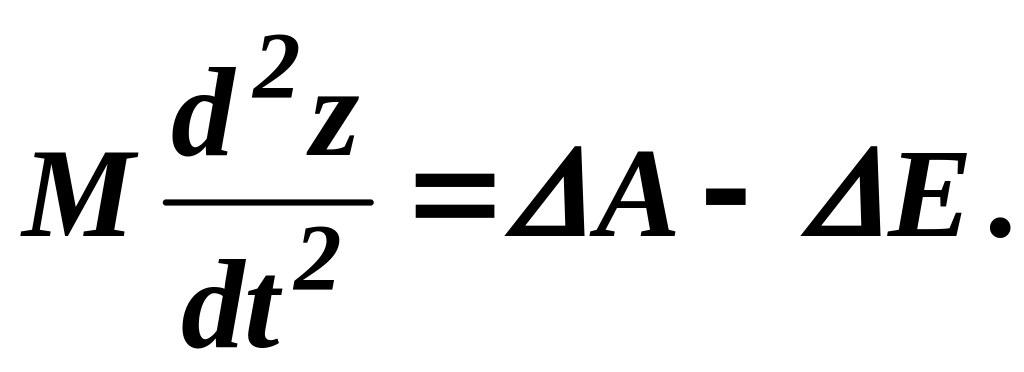
Так как

то уравнение регулятора принимает вид:

.

(3)

Для улучшения процесса регулирования в некоторых схемах вводят демпферы, называемыми катарактами (рис. 2), у которых степень демпфирования изменяются с помощью дросселя (перекрытие канала 3).

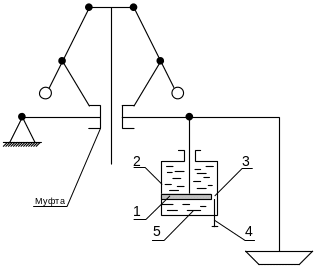
Рисунок 2 Катаракт:

1 – поршень; 2 – цилиндр; 3 – зазор; 4 – дроссель; 5 – масло.

Вследствие действия катаракты на муфту регулятора, возникает сила демпфирования:

где – коэффициент пропорциональности, учитывающий передаточное число от приложения силы катаракта к муфте. Знак минус указывает, что сила катаракты всегда направлена в сторону, противоположную движению муфты. С учетом силы уравнение регулятора примет вид:

.

(4)

Введем относительные переменные:

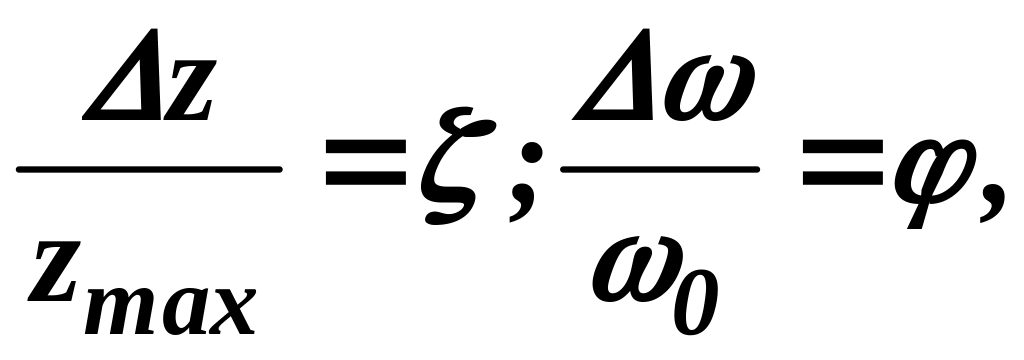
где – максимальный рабочий ход муфты, соответствующий максимальному статическому изменению регулируемой величины;

– значение регулируемой величины при режиме, который подвергается исследованию.

Тогда (4) примет вид:

или

(5)

где

где – время катаракты;

– время регулятора.

Если нет катаракты, то есть демпфирование отсутствует, то уравнение регулятора из–за с учетом постоянной скорости вращения станет таким:

.

(6)

Такое уравнение описывает гармонические колебания.

Для увеличения быстродействия регулятора необходимо увеличивать частоту собственных колебаний, то есть, чтобы можно было пренебречь его массой. А это требует , что достигается путем проектирования регулятора с малой приведенной массой и большой поддерживающей (силой упругости) силы.

Касательные и кориолисовы силы инерции

При выводе (5) не учитывались касательные и кориолисовы силы, действующие на центробежный регулятор.

Касательные силы инерции определяются как:

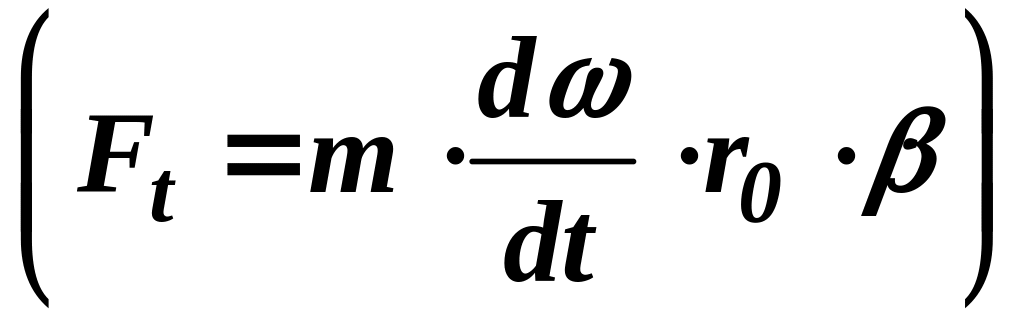, (6)

где – масса груза регулятора;

– радиус от силы вращения;

– передаточное число между валом машины и валом регулятора (для упрощения принимаем );

– угловая скорость вала турбины;

– ускорение вала турбины.

В коническом регуляторе эта сила направлена перпендикулярно к плоскости, проходящей через ось регулятора и центр тяжести груза и вызывает лишь трение в шарнирах, пропорциональное ускорению . Эта сила имеет направление с изменением направления движения муфты регулятора.

Кориолисова сила инерции, после начала движения муфты, вызывает тангенциальное движение в шарнирах и изменяется пропорционально изменению величины скорости относительного движения грузов, то есть влияния этой силы на движение регулятора будет такое же, как катаракта.

Величина кориолисовой силы инерции:

,

где – относительная скорость движения грузов в плоскости, проходящей через ось регулятора;

– угол между вектором υ_r и этой осью.

Примем

где – коэффициент, представляющий передаточное число между ходом муфты и ходом грузов регулятора.

Тангенциальные и кориолисовы силы вызывают давление в шарнирах, что в свою очередь приводит к трению и появлению зоны нечувствительности.

С учетом силы и уравнение регулятора запишется:

.

(7)

Здесь – отражает влияние касательных сил инерции.
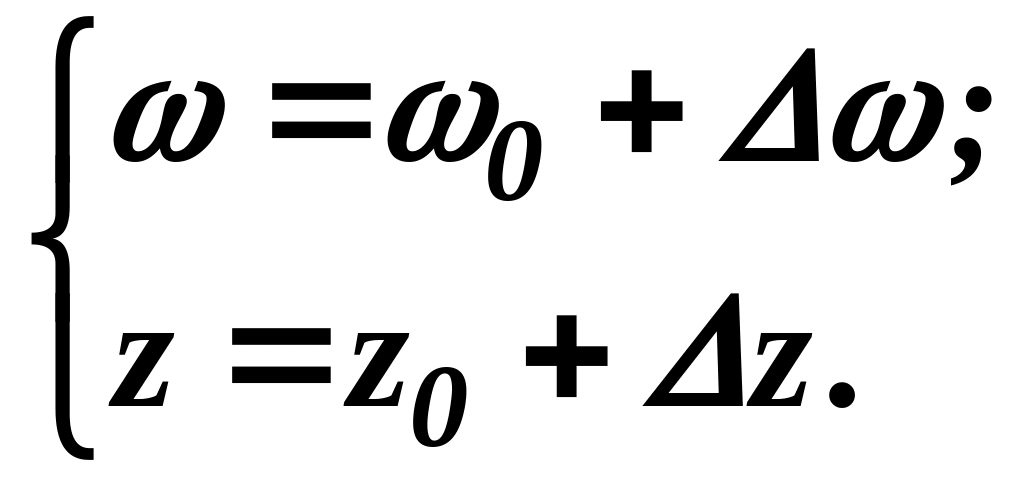
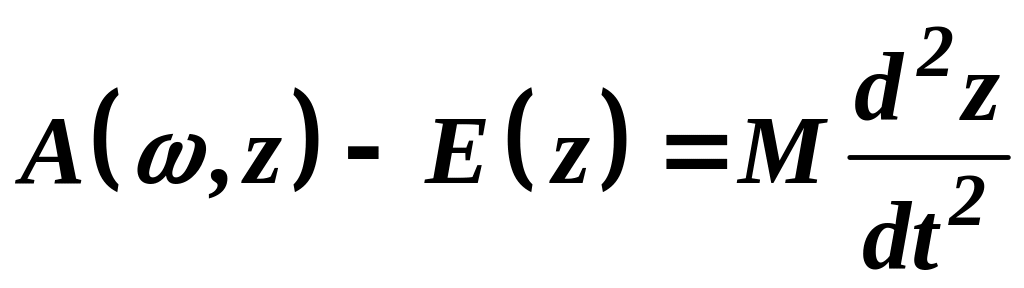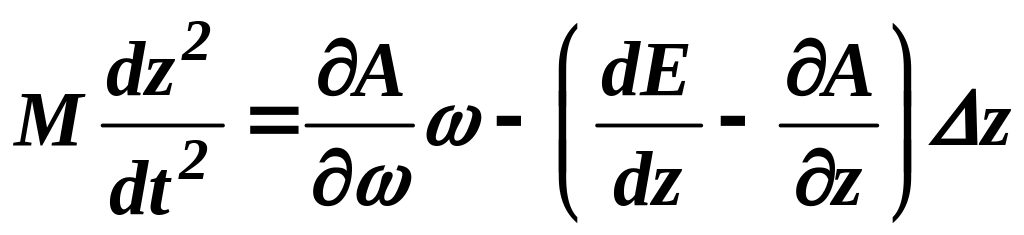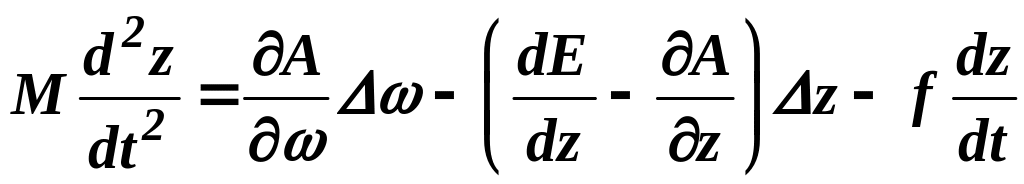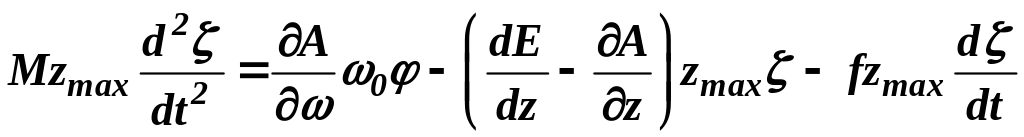
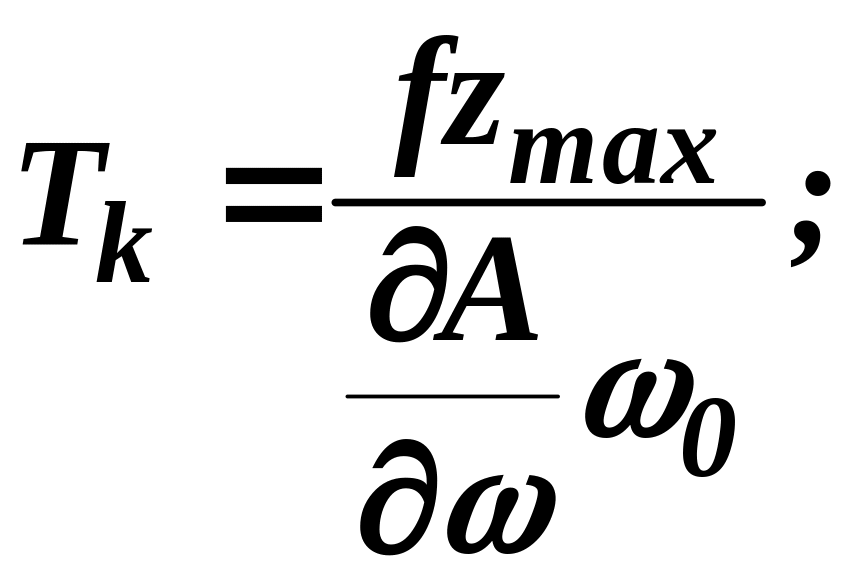
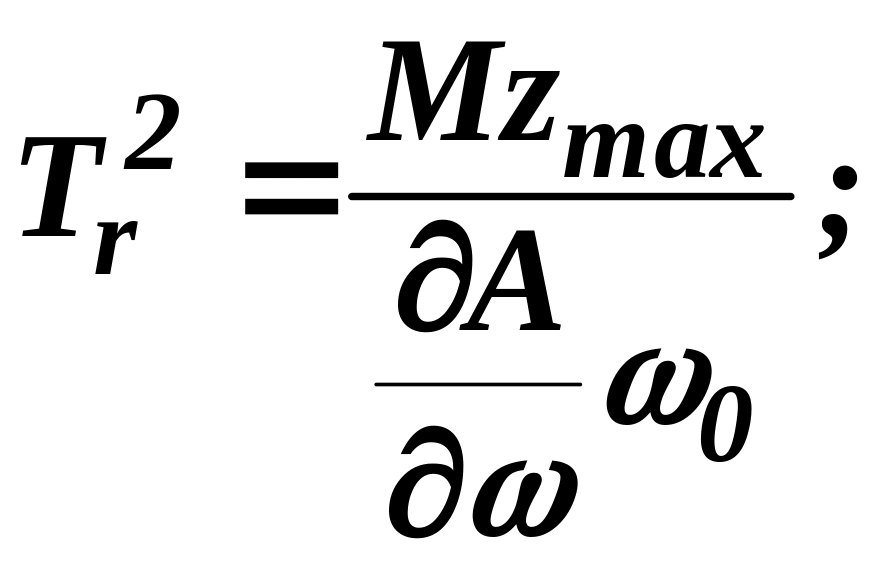
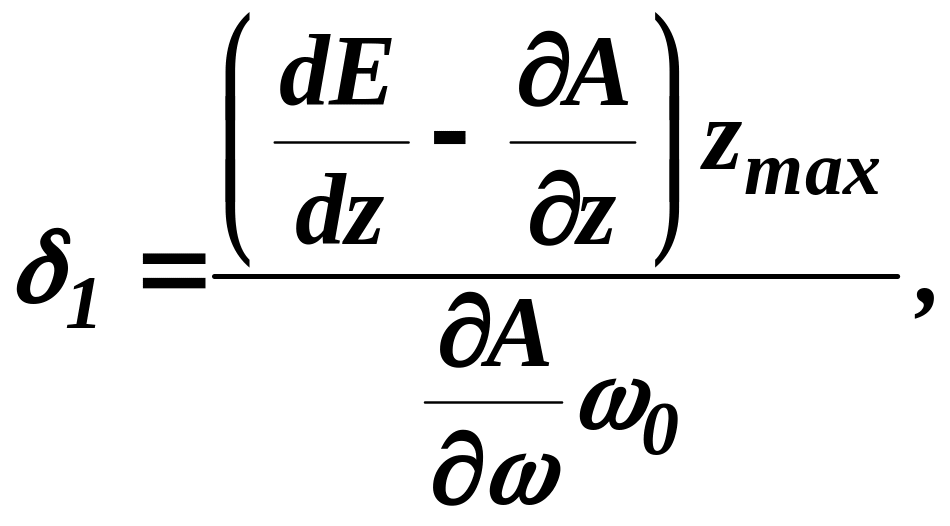
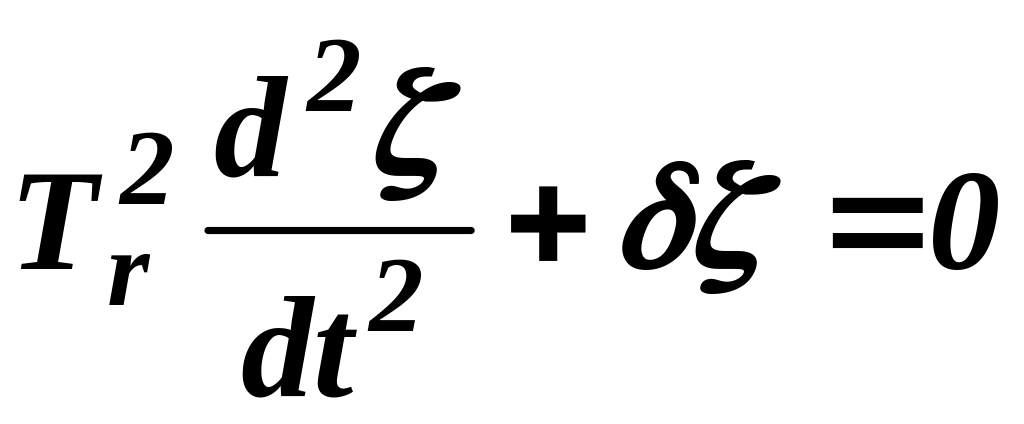