- •Содержание
- •1. Паспорт комплекта контрольно-оценочных средств
- •2. Результаты освоения учебной дисциплины, подлежащие проверке
- •3. Оценка освоения учебной дисциплины:
- •3.1. Формы и методы оценивания
- •III. Пакет экзаменатора
- •IV. Приложения. Контоль для оценки освоения дисциплины
- •Лист согласования Дополнения и изменения к комплекту кос на _______________ уч. Год
III. Пакет экзаменатора
Общие условия выполнения заданий
Количество обучающихся 30 чел.
Деление на подгруппы нет
Количество вариантов (пакетов) заданий для экзаменующихся: 30
Время выполнения каждого задания и максимальное время на экзамен
Часть А - 1 час.
Часть Б - 0,5 час.
Часть С - 1, 5 часа.
Всего на экзамен – 3 часа.
Условия выполнения заданий
Требования охраны труда: не требуется
Оборудование: ручка, лист А4, линейка, калькулятор
Литература для экзаменующихся:
Олофинская В. П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий : учебное пособие. – 2- е изд. – М. : ФОРУМ : ИНФРА-М, 2009. – 349 с. – (профессиональное образование).
Дополнительная литература для экзаменатора:
- Единой системы конструкторской документации (ЕСКД). Основное положения. – М. : 2010 – 344 с.: ил.
Задание 2.
Инструкция:
1. Внимательно прочитайте задание
2. Вспомните необходимые теоретические сведения из курса дисциплины
Экзаменационная ведомость
Типовая
Критерии оценки (разбалловка)
Часть А дает 1 балл;
Часть Б дает 2 балла;
Часть С дает 3 балла.
отлично |
27-35 б. |
хорошо |
19-26 б. |
удовлетворительно |
13-18 б. |
неудовлетворительно |
12 б. и менее |
Номер задания |
Эталон ответа |
Номер задания |
Эталон ответа |
|||
1 вариант |
2 вариант |
|||||
Часть А |
Часть А |
|||||
1 |
3 |
1 |
2 |
|||
2 |
3 |
2 |
4 |
|||
3 |
4 |
3 |
3 |
|||
4 |
2 |
4 |
2 |
|||
5 |
1 |
5 |
4 |
|||
6 |
4 |
6 |
3 |
|||
7 |
2 |
7 |
2 |
|||
8 |
2 |
8 |
3 |
|||
9 |
1 |
9 |
3 |
|||
10 |
1 |
10 |
4 |
|||
11 |
1 |
11 |
4 |
|||
12 |
2 |
12 |
2 |
|||
13 |
3 |
13 |
3 |
|||
14 |
1 |
14 |
3 |
|||
15 |
4 |
15 |
1 |
|||
16 |
3 |
16 |
1 |
|||
17 |
3 |
17 |
3 |
|||
18 |
4 |
18 |
3 |
|||
19 |
3 |
19 |
1 |
|||
20 |
2 |
20 |
1 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-в; 2- е; 3-с; 4 - d |
21 |
1-в; 2-а; 3-с; |
|||
22 |
1- б; 2 - в; 3- а |
22 |
1-в; 2- a; 3-f; 4- I; 5-е; 6-d; 7-c |
|||
23 |
1- с; 2 – в; 3-а |
23 |
1-в; 2-а; 3-г; 4-б |
|||
Часть С |
Часть С |
|||||
24) Решение: Дополнив пластинку до прямоугольника ABCD, разобьем ее на три части. Определим площади каждой части в см2 и координаты их центров тяжести в см: S1 = 28⋅20 = 560 см2; C1(0;10); S2 = 12⋅3,2 = 38,4 см2; C2(0;1,6); S3 = 18,4⋅10 = 184 см2; C3(0;15). Определим ординату центра тяжести пластинки с помощью метода отрицательных площадей:
|
24)Решение:
Допустимое
напряжение при растяжении
|
|||||
25) Решение
|
25) Решение. Рассмотрим равновесие балки. Проведем координатные оси x и y, и изобразим действующие на балку силы и реакции опоры А. Для определения ХА составим уравнение суммы проекций на ось x: Σ Fiх = 0 ХА – F• соs α = 0, откуда: ХА = F • соs 45 0= 8 • соs 450 = 5,6 кН. Для определения YA составим уравнение суммы проекций на ось y: Σ Fiy= 0 YА - F • sin α – q•а = 0, откуда: YА = F• sin 45 +2,6•q = 5,6 + 6,5 = 12,1 кН. Для определения момента MA составим уравнение суммы моментов относительно опоры А: Σ МА (Fi) = 0 МA - 2,6 • q•1,3 – 2,6 • F • sin 45– m = 0, откуда: МA = 2,6 • q•1,3 + 2,6 • F • sin 45+ m = 6,5•1,3 + 8•0,7•2,6 + 12 =8,45 + 14,56 + 12 = 35,01 кHм. Проверка: для проверки поставим точку К и составим уравнение суммы моментов относительно этой точки.Σ МК (Fi) = 0 МA - YА •2,6 + 2,6• q • – m = 0 35,01 – 31,46 + 8,45 – 12 = 0 |
|||||
26) Решение: Сечение шпонки для заданного диаметра вала принимаем: в=14 мм, h =9мм, t₂= 5, 5 мм. Длину шпонки принимаем на 4 мм меньше длины ступицы колеса l=71 – 4 = 67 мм. Расчетная длина шпонки Lp=l-b=67-14=53 мм.. Проверяем выбранную шпонку на смятие по формуле:
|
26) Решение. Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка. Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N1 (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса: откуда N1 = F. Очевидно, что на всем первом участке ( ) нормальная сила N1 постоянна по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е). Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N2 (рис. в). Проектируем все силы на ось бруса: откуда N2 = –F. Аналогично находим нормальные силы в сечении III – III (рис. г): откуда N3 = –F и в сечении IV – IV (рис. д): откуда N4 = 0. Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие. Для построения эпюры нормальных напряжений воспользуемся формулой для каждого участка: Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III).
|
|||||
3 вариант |
4 вариант |
|||||
Часть А |
Часть А |
|||||
1 |
1 |
1 |
2 |
|||
2 |
4 |
2 |
1 |
|||
3 |
1 |
3 |
4 |
|||
4 |
1 |
4 |
3 |
|||
5 |
1 |
5 |
4 |
|||
6 |
2 |
6 |
1 |
|||
7 |
2 |
7 |
4 |
|||
8 |
3 |
8 |
2 |
|||
9 |
1 |
9 |
3 |
|||
10 |
2 |
10 |
1 |
|||
11 |
2 |
11 |
1 |
|||
12 |
1 |
12 |
1 |
|||
13 |
1 |
13 |
2 |
|||
14 |
3 |
14 |
4 |
|||
15 |
2 |
15 |
4 |
|||
16 |
2 |
16 |
3 |
|||
17 |
1 |
17 |
1 |
|||
18 |
4 |
18 |
1 |
|||
19 |
2 |
19 |
1 |
|||
20 |
1 |
20 |
4 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-а;2-в;3-е;4-f |
21 |
1-в;2-а; 3-d |
|||
22 |
1-b; 2-f; 3-a; 4-g; 5-I; 6-d; 7-e; 8-c |
22 |
1-f; 2-d; 3-b; 4-e; 5-c; 6-a |
|||
23 |
1-а; 2-г; 3-д; 4-б,в |
23 |
1-а;2-с;3-в |
|||
Часть С |
Часть С |
|||||
24) Решение: Рассмотрим равновесие балки. Проведем координатные оси х и у, и изобразим действующие на балку силы и реакции опор. Для определения YA составим уравнение суммы моментов относительно опоры В: Σ МВ (Fi) = 0 -YA ·(l-а) - m + F· sin α ·( l – a – b) – q · а·а/2 = 0 Откуда: YA =( F· sin α ·( l – a – b) ) – m – q · а·а/2 ) / l-а =(34 · 0 ,7 9 -15 -3· 2· 1)/ /12 = (214,2 – 15 - 6) /12 = 16,1 кН. Для определения YВ составим уравнение суммы моментов относительно опоры А: Σ МА (Fi) = 0 – m -F· sin α · b + YВ · (l-а) - q · а · (l-а/2)= 0 Откуда: YВ =( m + F· sin α · b + q · а · (l-а/2)) / (l-а) = (15+34· 0,7· 3+3· 2· (14-1)) / 12 = =(15+71,4+78) / 12 = 164,4/12 = 13,7 кН. Для определения ХВ составим уравнение суммы проекций на ось х: Σ Fiх = 0 - ХВ + F· соs α = 0 откуда: ХВ = F· соs α = 34 · соs 450 = 23,8 кН. Проверка: Σ Fi у= 0 YA + YВ - F· sin α - q·а = 0 16,1 – 23,8 + 13,7 – 6 =0 |
24) 1. Намечаем характерные сечения. 2. Определяем поперечные силы в характерных сечениях.
4.
Вычисляем экстремальное значение
изгибающего момента в сечении, где
Строим
эпюру
|
|||||
25)
Решение:
Принимаем
суммарный статистический момент
площади рабочих поверхностей
|
25)
Решение: 1)предварительно
определим внутренний диаметр винта
из условия прочности на сжатие (с
учетом кручения). Для стали Ст5
|
|||||
26)
|
26)
|
|||||
5 вариант |
6 вариант |
|||||
Часть А |
Часть А |
|||||
1 |
2 |
1 |
2 |
|||
2 |
3 |
2 |
1 |
|||
3 |
3 |
3 |
1 |
|||
4 |
1 |
4 |
3 |
|||
5 |
1 |
5 |
1 |
|||
6 |
4 |
6 |
4 |
|||
7 |
4 |
7 |
1 |
|||
8 |
4 |
8 |
2 |
|||
9 |
2 |
9 |
1 |
|||
10 |
2 |
10 |
2 |
|||
11 |
2 |
11 |
3 |
|||
12 |
2 |
12 |
2 |
|||
13 |
1 |
13 |
2 |
|||
14 |
1 |
14 |
3 |
|||
15 |
4 |
15 |
2 |
|||
16 |
4 |
16 |
3 |
|||
17 |
2 |
17 |
2 |
|||
18 |
1 |
18 |
1 |
|||
19 |
4 |
19 |
1 |
|||
20 |
4 |
20 |
2 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-с;2-а;3-d |
21 |
1-в; 2-а; 3-с |
|||
22 |
1-с; 2-а;3-в |
22 |
1-в; 2- d; 3-a; 4-c |
|||
23 |
1-в;2-а;3-г;4-б |
23 |
1-в; 2-д; 3-г; 4-а; 5-б |
|||
Часть С |
Часть С |
|||||
24) Решение: Расстояние
а по
формуле |
24) Решение:
Ширина вкладыша b=(0,5…1,3)d=(0,5…1,3)40=20…52
мм. Ширину
вкладыша принимаем b=45мм.
Для бронзы
БрА9Ж3 принимаем [р]=15 Н/мм²,
[рυ]=12 Н/мм².
Наибольшая
радиальная нагрузка
по формуле
|
|||||
25) Решение: Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку A, а для другого – точку B: (1)∑ MA(Pi) = 0; -P1*AC - P2*AD + RB*AB = 0, (2)∑ MB(Pi) = 0; +P2*DB + P1*CB - RA*AB = 0. 4. Решая уравнения, из (1) находим RB = (P1*AC + P2*AD)/AB = (10*1 + 20*3,5)/5 = 16 кн; из (2) RA = (P2*DB + P1*CB)/AB = (20*1,5 + 10*4)/5 = 14 кн. 5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось у: ∑ Yi = 0; RA - P1 - P2 + RB = 0. Подставляя в это уравнение числовые значения, получаем тождество 14 - 10 - 20 + 16 = 0 или 0 = 0. Значит задача решена правильно. Реакции опор: RA = 14 кн и RB = 16 кн. |
25)
|
|||||
26)
|
26)
|
|||||
Вариант 7 |
Вариант 8 |
|||||
Часть А |
Часть А |
|||||
1 |
4 |
1 |
3 |
|||
2 |
2 |
2 |
3 |
|||
3 |
3 |
3 |
1 |
|||
4 |
2 |
4 |
4 |
|||
5 |
2 |
5 |
2 |
|||
6 |
2 |
6 |
1 |
|||
7 |
3 |
7 |
1 |
|||
8 |
1 |
8 |
3 |
|||
9 |
3 |
9 |
1 |
|||
10 |
3 |
10 |
1 |
|||
11 |
2 |
11 |
2 |
|||
12 |
2 |
12 |
2 |
|||
13 |
1 |
13 |
1 |
|||
14 |
4 |
14 |
1 |
|||
15 |
3 |
15 |
4 |
|||
16 |
2 |
16 |
2 |
|||
17 |
1 |
17 |
4 |
|||
18 |
1 |
18 |
1 |
|||
19 |
2 |
19 |
1 |
|||
20 |
2 |
20 |
3 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-с;2-d;3-а;4-в |
21 |
1-в; 2- a; 3-f; 4- I; 5-е; 6-d; 7-c |
|||
22 |
1-а;2-d; 3-с;4-в |
22 |
1-а; 2-в;3-с |
|||
23 |
1-а; 2-в; 3-б |
23 |
1-а; 2-б; 3-в |
|||
Часть С |
Часть С |
|||||
24)
Решение:
Сила, проходящая на один болт
|
24)
Решение:
момент
на ведущем валу равен
|
|||||
25)
|
25) Решение: Силу Р раскрадываем на две составляющие силы, соответствующие её проекциям на координатные оси. Распределённую нагрузку заменяем сосредоточенной силой Q
Из
уравнения (3) находится реактивный
момент связи в точке А
–
|
|||||
26)Определяем опорную реакцию в месте закрепления стержней: так
как
2. Вычисляем значение продольных сил:
3. Вычисляем значение нормальных напряжений:
4. Находим величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) всего стержня в целом:
|
26)
Решение.Для
определения внутренних усилий
разбиваем прямолинейный брус на
участки. Границами участков являются
точки продольной оси, соответствующие
изменению площади поперечного сечения
и точкам приложения сосредоточенных
сил. Из рассмотрения рис. а определяем,
что брус необходимо разбить на четыре
участка.Проводим сечение I – I.
Отбросим верхнюю часть бруса, ее
действие заменим нормальной
силой N1 (рис. б).
Запишем уравнение равновесия,
проектируя силы на ось бруса: Очевидно,
что на всем первом участке ( Аналогично
находим нормальные силы в
сечении III – III (рис. г):
и
в сечении IV – IV (рис. д):
Откладывая
в масштабе значения нормальных
сил N2, N3, N4 в
пределах соответствующих участков,
получаем эпюру нормальных сил (рис. е).
Полученную таким путем эпюру принято
штриховать прямыми линиями,
перпендикулярными к оси бруса. Каждая
такая линия в принятом масштабе дает
величину нормальной силы в соответствующем
поперечном сечении бруса. Знак «плюс»
показывает, что в пределах данного
участка – растяжение, а знак «минус»
– сжатие. Для построения эпюры
нормальных напряжений
Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III) |
|||||
Вариант 9 |
Вариант 10 |
|||||
Часть А |
Часть А |
|||||
1 |
3 |
1 |
1 |
|||
2 |
3 |
2 |
4 |
|||
3 |
1 |
3 |
2 |
|||
4 |
3 |
4 |
1 |
|||
5 |
4 |
5 |
1 |
|||
6 |
2 |
6 |
1 |
|||
7 |
4 |
7 |
3 |
|||
8 |
1 |
8 |
4 |
|||
9 |
1 |
9 |
2 |
|||
10 |
2 |
10 |
2 |
|||
11 |
1 |
11 |
1 |
|||
12 |
1 |
12 |
4 |
|||
13 |
4 |
13 |
2 |
|||
14 |
1 |
14 |
2 |
|||
15 |
1 |
15 |
2 |
|||
16 |
1 |
16 |
3 |
|||
17 |
1 |
17 |
1 |
|||
18 |
1 |
18 |
3 |
|||
19 |
1 |
19 |
1 |
|||
20 |
1 |
20 |
2 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-с;2-а |
21 |
1-d;2-с;3-в |
|||
22 |
1-а; 2-с; 3-в |
22 |
1-д; 2-б; 3-а; 4-г; 5-в |
|||
23 |
1-в; 2-с; 3-а |
23 |
1-с; 2-а; 3-в |
|||
Часть С |
Часть С |
|||||
24) Решение. 1.
Используя формулу сечение
1 – 1 сечение
2 – 2 сечение
3 – 3
2.
Проводим рядом с брусом ось, параллельную
его продольной оси, и, выбрав масштаб,
откладываем по длине каждого участка
найденные значения продольных
сил 3.
Определяем опасное сечение – сечение,
в котором нормальные напряжения
максимальны (для пластичных материалов
берем по абсолютной величине),
т.е.
|
24)
Решение:
Для
диаметра вала d=50мм
принимаем
размеры сечения шпонки
в=14мм,h=9
мм. Глубина
паза t₁=
5,5 мм. Выбираем
длину шпонки. При длине ступицы
принимаем длину шпонки l=63
мм. Допускаемой
напряжение смятия
|
|||||
25) Решение: Допустимое напряжение при растяжении . Расчетный диаметр резьбы болта по формуле: . Принимаем резьбу М20 с шагом р=2,5 мм, для которой |
25)
2.
Изобразим оси координат x и y
3.Силу F заменяем
ее составляющими
b) Определяем другую вертикальную реакцию:
6. Проверяем правильность найденных результатов:
Условие
равновесия |
|||||
26)
|
26)
1. Определяем внутренние продольные силы. Имеем два силовых участка длиной (а + b) и c. Для первого участка, имеем
для второго участка:
Выбираем
масштаб и строим эпюру 2. Вычисляем нормальные напряжения. На участках а и b площадь поперечного сечения одинакова и равна 2А=20 см2. Тогда
на участке с:
Выбираем
масштаб и строим эпюру
|
|||||
11 вариант |
12 вариант |
|||||
Часть А |
Часть А |
|||||
1 |
2 |
1 |
4 |
|||
2 |
3 |
2 |
1 |
|||
3 |
2 |
3 |
1 |
|||
4 |
4 |
4 |
2 |
|||
5 |
1 |
5 |
2 |
|||
6 |
1 |
6 |
2 |
|||
7 |
3 |
7 |
2 |
|||
8 |
1 |
8 |
3 |
|||
9 |
1 |
9 |
4 |
|||
10 |
3 |
10 |
4 |
|||
11 |
2 |
11 |
2 |
|||
12 |
2 |
12 |
1 |
|||
13 |
1 |
13 |
2 |
|||
14 |
4 |
14 |
2 |
|||
15 |
1 |
15 |
4 |
|||
16 |
1 |
16 |
1 |
|||
17 |
3 |
17 |
4 |
|||
18 |
2 |
18 |
1 |
|||
19 |
4 |
19 |
4 |
|||
20 |
2 |
20 |
2 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-в; 2-а; 3- с; 4- d |
21 |
1-б; 2-в; 3-а |
|||
22 |
1-a; 2 – в ; 3-б |
22 |
1-в; 2-а; 3- f;4-I;5-e; 6-d; 7-c |
|||
23 |
1-f;2-d;3-b; 4-e;5-c; 6-a |
23 |
1-c; 2-a; 3-d |
|||
Часть С |
Часть С |
|||||
24) Решение: Дополнив пластинку до прямоугольника ABCD, разобьем ее на три части. Определим площади каждой части в см2 и координаты их центров тяжести в см: S1 = 28⋅20 = 560 см2; C1(0;10); S2 = 12⋅3,2 = 38,4 см2; C2(0;1,6); S3 = 18,4⋅10 = 184 см2; C3(0;15). Определим ординату центра тяжести пластинки с помощью метода отрицательных площадей:
|
24) Решение
|
|||||
24)Определяем опорную реакцию в месте закрепления стержней: так как то
2. Вычисляем значение продольных сил:
3. Вычисляем значение нормальных напряжений:
4. Находим величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) всего стержня в целом:
|
25) Решение: момент на ведущем валу равен . Диаметр малого шкива определяем по формуле: . По ГОСТ 17383-73 округляем до ближайшего меньшего значения. Принимаем D₁=315мм. Определяем диаметр большего шкива по формуле: . Принимаем по стандарту D₂=800мм. Определяем скорость ремня по формуле: |
|||||
26) Решение: 1)предварительно определим внутренний диаметр винта из условия прочности на сжатие (с учетом кручения). Для стали Ст5 . 2) По ГОСТ 9484-81 находим с ближайшим большим d₁ : d=60 мм;d₁ = 51мм; d₂=56; ρ=8 мм. 3) Определим необходимую высоту гайки из расчета резьбы на изностойкость
|
26)
|
|||||
13 вариант |
14 вариант |
|||||
Часть А |
Часть А |
|||||
1 |
1 |
1 |
2 |
|||
2 |
2 |
2 |
3 |
|||
3 |
2 |
3 |
3 |
|||
4 |
2 |
4 |
1 |
|||
5 |
4 |
5 |
1 |
|||
6 |
3 |
6 |
4 |
|||
7 |
1 |
7 |
1 |
|||
8 |
2 |
8 |
4 |
|||
9 |
2 |
9 |
2 |
|||
10 |
2 |
10 |
3 |
|||
11 |
4 |
11 |
1 |
|||
12 |
1 |
12 |
1 |
|||
13 |
2 |
13 |
4 |
|||
14 |
3 |
14 |
4 |
|||
15 |
1 |
15 |
3 |
|||
16 |
1 |
16 |
1 |
|||
17 |
3 |
17 |
2 |
|||
18 |
1 |
18 |
2 |
|||
19 |
1 |
19 |
2 |
|||
20 |
1 |
20 |
3 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-с; 2- в; 3-а |
21 |
1-в;2-a;3-c |
|||
22 |
1-а;2-b; 3- c |
22 |
1-a;2-б;3-в |
|||
23 |
1-a;2-c;3-b |
23 |
1-c;2-a;3-b |
|||
Часть С |
Часть С |
|||||
24) Решение: Сечение шпонки для заданного диаметра вала принимаем: в=14 мм, h =9мм, t₂= 5, 5 мм. Длину шпонки принимаем на 4 мм меньше длины ступицы колеса l=71 – 4 = 67 мм. Расчетная длина шпонки Lp=l-b=67-14=53 мм.. Проверяем выбранную шпонку на смятие по формуле:
|
24)Решение: Допустимое напряжение при растяжении . Расчетный диаметр резьбы болта по формуле: . Принимаем резьбу М20 с шагом р=2,5 мм, для которой |
|||||
25) Решение: Силу Р раскрадываем на две составляющие силы, соответствующие её проекциям на координатные оси. Распределённую нагрузку заменяем сосредоточенной силой Q Составляются уравнения равновесия статики, используется I – основная форма условий равновесия, в которой равны нулю: проекции главного вектора на координатные оси и главный момент относительно произвольного центра (1) ; (2) ; (2) . (3)Из уравнения (1) определяется составляющая реакции связи в точке А – Из уравнения (2) находится составляющая реакции связи в точке А – Из уравнения (3) находится реактивный момент связи в точке А – Проверка: Для проверки составляется уравнение равновесия моментов относительно произвольной точки, например, В, через которую не проходит линия действия ни одной силы. Ответ: кН.м .Знак минус у силовых факторов означает то, что они в действительности направлены в сторону, противоположную той, которая указана на расчётной схеме. |
25)
Решение.Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка.Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N1 (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса: откуда N1 = F. Очевидно, что на всем первом участке ( ) нормальная сила N1 постоянна по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е). Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N2 (рис. в). Проектируем все силы на ось бруса: откуда N2 = –F. Аналогично находим нормальные силы в сечении III – III (рис. г): откуда N3 = –F и в сечении IV – IV (рис. д): откуда N4 = 0. Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие. Для построения эпюры нормальных напряжений воспользуемся формулой для каждого участка:
Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III) |
|||||
26) 1. Намечаем характерные сечения. 2. Определяем поперечные силы в характерных сечениях. 3. Строим эпюру .Характер эпюры, то есть тот факт, что эпюра пересекает ось, говорит о том, что в этом сечении момент будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки : Определяем изгибающие моменты в характерных сечениях.
4. Вычисляем экстремальное значение изгибающего момента в сечении, где :
Строим эпюру .
|
26)
|
|||||
Вариант 15 |
Вариант 16 |
|||||
Часть А |
Часть А |
|||||
1 |
3 |
1 |
2 |
|||
2 |
1 |
2 |
3 |
|||
3 |
4 |
3 |
4 |
|||
4 |
1 |
4 |
2 |
|||
5 |
3 |
5 |
1 |
|||
6 |
1 |
6 |
2 |
|||
7 |
2 |
7 |
2 |
|||
8 |
1 |
8 |
3 |
|||
9 |
2 |
9 |
1 |
|||
10 |
1 |
10 |
2 |
|||
11 |
2 |
11 |
3 |
|||
12 |
4 |
12 |
2 |
|||
13 |
3 |
13 |
2 |
|||
14 |
2 |
14 |
1 |
|||
15 |
1 |
15 |
1 |
|||
16 |
4 |
16 |
1 |
|||
17 |
3 |
17 |
3 |
|||
18 |
1 |
18 |
1 |
|||
19 |
1 |
19 |
2 |
|||
20 |
1 |
20 |
3 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-b;2-a;3-f;4-I;5-e;6-d;7-c |
21 |
1-в; 2-а; 3-г; 4-б; |
|||
22 |
1-c;2-a |
22 |
1-а; 2- с; 3 –b; |
|||
23 |
1-в;2-а; 3-г; 4-б; |
23 |
1-b; 2-а; 3-c |
|||
Часть С |
Часть С |
|||||
24) Решение. Рассмотрим равновесие балки. Проведем координатные оси x и y, и изобразим действующие на балку силы и реакции опоры А. Для определения ХА составим уравнение суммы проекций на ось x: Σ Fiх = 0 ХА – F• соs α = 0, откуда: ХА = F • соs 45 0= 8 • соs 450 = 5,6 кН. Для определения YA составим уравнение суммы проекций на ось y: Σ Fiy= 0 YА - F • sin α – q•а = 0, откуда: YА = F• sin 45 +2,6•q = 5,6 + 6,5 = 12,1 кН. Для определения момента MA составим уравнение суммы моментов относительно опоры А: Σ МА (Fi) = 0 МA - 2,6 • q•1,3 – 2,6 • F • sin 45– m = 0, откуда: МA = 2,6 • q•1,3 + 2,6 • F • sin 45+ m = 6,5•1,3 + 8•0,7•2,6 + 12 =8,45 + 14,56 + 12 = 35,01 кHм. Проверка: для проверки поставим точку К и составим уравнение суммы моментов относительно этой точки.Σ МК (Fi) = 0 МA - YА •2,6 + 2,6• q • – m = 0 35,01 – 31,46 + 8,45 – 12 = 0 |
24) Решение. Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка. Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N1 (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса: откуда N1 = F. Очевидно, что на всем первом участке ( ) нормальная сила N1 постоянна по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е). Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N2 (рис. в). Проектируем все силы на ось бруса: откуда N2 = –F. Аналогично находим нормальные силы в сечении III – III (рис. г): откуда N3 = –F и в сечении IV – IV (рис. д): откуда N4 = 0. Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие. Для построения эпюры нормальных напряжений воспользуемся формулой для каждого участка: Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III).
|
|||||
25) Решение. 1. Используя формулу , для каждого из 3-х участков получим (рис. а): сечение 1 – 1 = – 4000 кг = –40 кН, сечение 2 – 2 = – 4000 + 3000 = –1000 кг = –10 кН, сечение 3 – 3 = – 4000 + 3000 + 8000=7000кг = 70 кН. 2. Проводим рядом с брусом ось, параллельную его продольной оси, и, выбрав масштаб, откладываем по длине каждого участка найденные значения продольных сил , и , т.е. строим эпюру N (рис. б). 3. Определяем опасное сечение – сечение, в котором нормальные напряжения максимальны (для пластичных материалов берем по абсолютной величине), т.е. ,где А – площадь поперечного сечения бруса. В нашем случае для всех трех участков площадь поперечного сечения А постоянна и по абсолютной величине N3>N2>N1. Опасное сечение – любое сечение участка 3, где = 7000 кг = 70 кН. Тогда из условия прочности на растяжение и сжатие для расчета площади поперечного сечения применим формулу ; .Отсюда
|
25) Решение: Допустимое напряжение при растяжении . Расчетный диаметр резьбы болта по формуле: . Принимаем резьбу М20 с шагом р=2,5 мм, для которой |
|||||
26) Решение: Ширина вкладыша b=(0,5…1,3)d=(0,5…1,3)40=20…52 мм. Ширину вкладыша принимаем b=45мм. Для бронзы БрА9Ж3 принимаем [р]=15 Н/мм², [рυ]=12 Н/мм². Наибольшая радиальная нагрузка по формуле . Окружная скорость цапфы вала . Проверяем подшипник на отсутствие заедание по формуле , что допустимо. |
26)
|
|||||
Вариант 17 |
Вариант 18 |
|||||
Часть А |
Часть А |
|||||
1 |
4 |
1 |
1 |
|||
2 |
1 |
2 |
2 |
|||
3 |
3 |
3 |
2 |
|||
4 |
3 |
4 |
1 |
|||
5 |
3 |
5 |
3 |
|||
6 |
3 |
6 |
1 |
|||
7 |
3 |
7 |
3 |
|||
8 |
2 |
8 |
1 |
|||
9 |
2 |
9 |
1 |
|||
10 |
2 |
10 |
3 |
|||
11 |
4 |
11 |
1 |
|||
12 |
4 |
12 |
3 |
|||
13 |
2 |
13 |
3 |
|||
14 |
2 |
14 |
2 |
|||
15 |
3 |
15 |
1 |
|||
16 |
2 |
16 |
1 |
|||
17 |
1 |
17 |
1 |
|||
18 |
2 |
18 |
2 |
|||
19 |
4 |
19 |
1 |
|||
20 |
1 |
20 |
1 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-a;2-b;3-e;4-f |
21 |
1-b;2-f;3-a;4-g;5-I; 6-d; 7-e;8-c |
|||
22 |
1-b;2-c;3-a |
22 |
1-d; 2-c; 3-b |
|||
23 |
1-b;2-d;3-a;4-c |
23 |
1-в; 2-д; 3–г; 4-а;5-б |
|||
Часть С |
Часть С |
|||||
24) Решение: Рассмотрим равновесие балки. Проведем координатные оси х и у, и изобразим действующие на балку силы и реакции опор. Для определения YA составим уравнение суммы моментов относительно опоры В: Σ МВ (Fi) = 0 -YA ·(l-а) - m + F· sin α ·( l – a – b) – q · а·а/2 = 0 Откуда: YA =( F· sin α ·( l – a – b) ) – m – q · а·а/2 ) / l-а =(34 · 0 ,7 9 -15 -3· 2· 1)/ /12 = (214,2 – 15 - 6) /12 = 16,1 кН. Для определения YВ составим уравнение суммы моментов относительно опоры А: Σ МА (Fi) = 0 – m -F· sin α · b + YВ · (l-а) - q · а · (l-а/2)= 0 Откуда: YВ =( m + F· sin α · b + q · а · (l-а/2)) / (l-а) = (15+34· 0,7· 3+3· 2· (14-1)) / 12 = =(15+71,4+78) / 12 = 164,4/12 = 13,7 кН. Для определения ХВ составим уравнение суммы проекций на ось х: Σ Fiх = 0 - ХВ + F· соs α = 0 откуда: ХВ = F· соs α = 34 · соs 450 = 23,8 кН. Проверка: Σ Fi у= 0 YA + YВ - F· sin α - q·а = 0 16,1 – 23,8 + 13,7 – 6 =0 |
24) Решение: Принимаем суммарный статистический момент площади рабочих поверхностей . Прочность неподвижного соединения проверяем по напряжениям смятия. Для соединений с незакаленными поверхностями при спокойной нагрузке принимаем допускаемое напряжение на смятие . Расчетное напряжение смятия шлицев по формуле . Условие прочности соединения удовлетворяются. |
|||||
25) Решение: Для диаметра вала d=50мм принимаем размеры сечения шпонки в=14мм,h=9 мм. Глубина паза t₁= 5,5 мм. Выбираем длину шпонки. При длине ступицы принимаем длину шпонки l=63 мм. Допускаемой напряжение смятия . Расчетное напряжение смятия шпонки по формуле: , что удовлетворяет условию прочности.
|
25) 2. Изобразим оси координат x и y 3.Силу F заменяем ее составляющими и .Равнодействующая qСD равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника переносится по линии своего действия в середину участка CD, в точку К. 4. Освобождаем балку от опор, заменив их опорными реакциями. 5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор. a) Из уравнения моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:
кН b) Определяем другую вертикальную реакцию:
кН c) Определяем горизонтальную реакцию: ; кН 6. Проверяем правильность найденных результатов: . Условие равновесия выполняется, следовательно, реакции опор найдены верно. |
|||||
26)
|
26)
Решение.Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка.Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N1 (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса: откуда N1 = F. Очевидно, что на всем первом участке ( ) нормальная сила N1 постоянна по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е). Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N2 (рис. в). Проектируем все силы на ось бруса: откуда N2 = –F. Аналогично находим нормальные силы в сечении III – III (рис. г): откуда N3 = –F и в сечении IV – IV (рис. д): откуда N4 = 0. Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие. Для построения эпюры нормальных напряжений воспользуемся формулой для каждого участка:
Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III) |
|||||
Вариант 19 |
Вариант 20 |
|||||
Часть А |
Часть А |
|||||
1 |
3 |
1 |
4 |
|||
2 |
2 |
2 |
1 |
|||
3 |
1 |
3 |
2 |
|||
4 |
3 |
4 |
2 |
|||
5 |
1 |
5 |
1 |
|||
6 |
2 |
6 |
1 |
|||
7 |
4 |
7 |
3 |
|||
8 |
1 |
8 |
4 |
|||
9 |
4 |
9 |
2 |
|||
10 |
2 |
10 |
1 |
|||
11 |
1 |
11 |
1 |
|||
12 |
1 |
12 |
2 |
|||
13 |
2 |
13 |
4 |
|||
14 |
2 |
14 |
3 |
|||
15 |
3 |
15 |
2 |
|||
16 |
1 |
16 |
2 |
|||
17 |
1 |
17 |
4 |
|||
18 |
4 |
18 |
1 |
|||
19 |
4 |
19 |
1 |
|||
20 |
4 |
20 |
1 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-а; 2-г; 3-д; 4-б,в; |
21 |
1-в; 2-а; 3- б; |
|||
22 |
1-д; 2-б; 3-а; 4-г; 5-в; |
22 |
1-с ;2 – а; 3-в; |
|||
23 |
1-с; 2-d; 3-a; 4-b; |
23 |
1-a; 2-d; 3-c; 4-b; |
|||
Часть С |
Часть С |
|||||
24)
|
24) 1. Намечаем характерные сечения. 2. Определяем поперечные силы в характерных сечениях. 3. Строим эпюру .Характер эпюры, то есть тот факт, что эпюра пересекает ось, говорит о том, что в этом сечении момент будет иметь экстремальное значение. Действительно, пересечение эпюры с осью z означает, что в этом сечении , а из курса математики известно, что если производная функции равна нулю, то сама функция в данной точке имеет экстремальное значение.Для определения положения “нулевого” сечения необходимо величину расположенной слева от него ординаты эпюры разделить на интенсивность распределенной нагрузки : Определяем изгибающие моменты в характерных сечениях.
4. Вычисляем экстремальное значение изгибающего момента в сечении, где :
Строим эпюру .
|
|||||
26)
|
25) Решение: Дополнив пластинку до прямоугольника ABCD, разобьем ее на три части. Определим площади каждой части в см2 и координаты их центров тяжести в см: S1 = 28⋅20 = 560 см2; C1(0;10); S2 = 12⋅3,2 = 38,4 см2; C2(0;1,6); S3 = 18,4⋅10 = 184 см2; C3(0;15). Определим ординату центра тяжести пластинки с помощью метода отрицательных площадей:
|
|||||
26) Решение: Ширина вкладыша b=(0,5…1,3)d=(0,5…1,3)40=20…52 мм. Ширину вкладыша принимаем b=45мм. Для бронзы БрА9Ж3 принимаем [р]=15 Н/мм², [рυ]=12 Н/мм². Наибольшая радиальная нагрузка по формуле . Окружная скорость цапфы вала . Проверяем подшипник на отсутствие заедание по формуле , что допустимо. |
26)
Решение:
Определяем
допускаемое напряжение для сварного
шва.
|
|||||
Вариант 21 |
Вариант 22 |
|||||
Часть А |
Часть А |
|||||
1 |
4 |
1 |
2 |
|||
2 |
2 |
2 |
4 |
|||
3 |
3 |
3 |
4 |
|||
4 |
4 |
4 |
4 |
|||
5 |
3 |
5 |
2 |
|||
6 |
1 |
6 |
1 |
|||
7 |
4 |
7 |
2 |
|||
8 |
3 |
8 |
3 |
|||
9 |
2 |
9 |
1 |
|||
10 |
4 |
10 |
4 |
|||
11 |
2 |
11 |
3 |
|||
12 |
1 |
12 |
2 |
|||
13 |
4 |
13 |
2 |
|||
14 |
1 |
14 |
3 |
|||
15 |
2 |
15 |
2 |
|||
16 |
4 |
16 |
4 |
|||
17 |
2 |
17 |
1 |
|||
18 |
1 |
18 |
3 |
|||
19 |
1 |
19 |
1 |
|||
20 |
1 |
20 |
1 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-f; 2-d; 3-b;4-e; 5-c;6-a |
21 |
1-a; 2-c; 3-в; |
|||
22 |
1-b; 2-e; 3-c; 4-d |
22 |
1-c; 2-в; 3-a |
|||
23 |
1-а; 2-в; 3-б; |
23 |
1-a; 2- в; 3-c; |
|||
Часть С |
Часть С |
|||||
24) Решение: Определяем допускаемое напряжение для сварного шва. . По формуле найдем ширину полос : . Округляем до параметрического ряда и принимаем b=120 мм. Условие прочности шва . Условие прочности шва соблюдается (142,4 МПа <144 МПа). |
24)
|
|||||
25)
1. Определяем внутренние продольные силы. Имеем два силовых участка длиной (а + b) и c. Для первого участка, имеем = = 15·103 кг = 150 кН (растяжение); для второго участка: = – = 15 – 20 = –5 кг = –50 кН (сжатие). Выбираем масштаб и строим эпюру (рис. б). 2. Вычисляем нормальные напряжения. На участках а и b площадь поперечного сечения одинакова и равна 2А=20 см2. Тогда
на участке с:
Выбираем масштаб и строим эпюру .
|
25) Решение
|
|||||
26)
|
26) Решение: Сила, проходящая на один болт . Допускаемое напряжение среза . Диаметр стержня болта: . Принимаем 6 болтов М8. |
|||||
Вариант 23 |
Вариант 24 |
|||||
Часть А |
Часть Б |
|||||
1 |
3 |
1 |
2 |
|||
2 |
2 |
2 |
3 |
|||
3 |
2 |
3 |
3 |
|||
4 |
2 |
4 |
1 |
|||
5 |
3 |
5 |
1 |
|||
6 |
3 |
6 |
4 |
|||
7 |
1 |
7 |
1 |
|||
8 |
2 |
8 |
4 |
|||
9 |
1 |
9 |
2 |
|||
10 |
2 |
10 |
3 |
|||
11 |
1 |
11 |
1 |
|||
12 |
3 |
12 |
4 |
|||
13 |
2 |
13 |
4 |
|||
14 |
4 |
14 |
4 |
|||
15 |
2 |
15 |
2 |
|||
16 |
1 |
16 |
4 |
|||
17 |
1 |
17 |
1 |
|||
18 |
1 |
18 |
1 |
|||
19 |
1 |
19 |
1 |
|||
20 |
1 |
20 |
2 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-c;2-a;3-b |
21 |
1-c;2-a;3-b |
|||
22 |
1-b;2a;3-c;4-d |
22 |
1-b;2-a;3-c |
|||
23 |
1-в; 2-а |
23 |
1-a; 2-б;3-в |
|||
Часть С |
Часть С |
|||||
24) Решение: Расстояние а по формуле |
24) Решение: Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку A, а для другого – точку B: (1)∑ MA(Pi) = 0; -P1*AC - P2*AD + RB*AB = 0, (2)∑ MB(Pi) = 0; +P2*DB + P1*CB - RA*AB = 0. 4. Решая уравнения, из (1) находим RB = (P1*AC + P2*AD)/AB = (10*1 + 20*3,5)/5 = 16 кн; из (2) RA = (P2*DB + P1*CB)/AB = (20*1,5 + 10*4)/5 = 14 кн. 5. Проверим правильность решения, составив уравнение проекций сил на вертикальную ось у: ∑ Yi = 0; RA - P1 - P2 + RB = 0. Подставляя в это уравнение числовые значения, получаем тождество 14 - 10 - 20 + 16 = 0 или 0 = 0. Значит задача решена правильно. Реакции опор: RA = 14 кн и RB = 16 кн. |
|||||
25) Решение. Рассмотрим равновесие балки. Проведем координатные оси x и y, и изобразим действующие на балку силы и реакции опоры А. Для определения ХА составим уравнение суммы проекций на ось x: Σ Fiх = 0 ХА – F• соs α = 0, откуда: ХА = F • соs 45 0= 8 • соs 450 = 5,6 кН. Для определения YA составим уравнение суммы проекций на ось y: Σ Fiy= 0 YА - F • sin α – q•а = 0, откуда: YА = F• sin 45 +2,6•q = 5,6 + 6,5 = 12,1 кН. Для определения момента MA составим уравнение суммы моментов относительно опоры А: Σ МА (Fi) = 0 МA - 2,6 • q•1,3 – 2,6 • F • sin 45– m = 0, откуда: МA = 2,6 • q•1,3 + 2,6 • F • sin 45+ m = 6,5•1,3 + 8•0,7•2,6 + 12 =8,45 + 14,56 + 12 = 35,01 кHм. Проверка: для проверки поставим точку К и составим уравнение суммы моментов относительно этой точки.Σ МК (Fi) = 0 МA - YА •2,6 + 2,6• q • – m = 0 35,01 – 31,46 + 8,45 – 12 = 0 |
25) Решение: Сечение шпонки для заданного диаметра вала принимаем: в=14 мм, h =9мм, t₂= 5, 5 мм. Длину шпонки принимаем на 4 мм меньше длины ступицы колеса l=71 – 4 = 67 мм. Расчетная длина шпонки Lp=l-b=67-14=53 мм.. Проверяем выбранную шпонку на смятие по формуле:
|
|||||
26)
|
26)Определяем опорную реакцию в месте закрепления стержней: так как то
2. Вычисляем значение продольных сил:
3. Вычисляем значение нормальных напряжений:
4. Находим величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) всего стержня в целом:
|
|||||
Вариант 25 |
Вариант 26 |
|||||
Часть А |
Часть А |
|||||
1 |
3 |
1 |
2 |
|||
2 |
4 |
2 |
4 |
|||
3 |
2 |
3 |
1 |
|||
4 |
1 |
4 |
1 |
|||
5 |
1 |
5 |
2 |
|||
6 |
3 |
6 |
2 |
|||
7 |
4 |
7 |
3 |
|||
8 |
4 |
8 |
1 |
|||
9 |
1 |
9 |
1 |
|||
10 |
2 |
10 |
2 |
|||
11 |
2 |
11 |
2 |
|||
12 |
2 |
12 |
2 |
|||
13 |
4 |
13 |
2 |
|||
14 |
2 |
14 |
1 |
|||
15 |
3 |
15 |
3 |
|||
16 |
1 |
16 |
4 |
|||
17 |
1 |
17 |
4 |
|||
18 |
1 |
18 |
1 |
|||
19 |
3 |
19 |
3 |
|||
20 |
1 |
20 |
1 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-в; 2-а; 3-г; 4-б; |
21 |
1-b; 2 – a; 3-c |
|||
22 |
1-b; 2-a; 3-f; 4-I; 5-e; 6-d |
22 |
1-в; 2-а; 3-г; 4-б; |
|||
23 |
1-c; 2-a |
23 |
1-а; 2-c; 3-b |
|||
Часть С |
Часть С |
|||||
24)
|
24) Решение: Ширина вкладыша b=(0,5…1,3)d=(0,5…1,3)40=20…52 мм. Ширину вкладыша принимаем b=45мм. Для бронзы БрА9Ж3 принимаем [р]=15 Н/мм², [рυ]=12 Н/мм². Наибольшая радиальная нагрузка по формуле . Окружная скорость цапфы вала . Проверяем подшипник на отсутствие заедание по формуле , что допустимо. |
|||||
25)Решение: Допустимое напряжение при растяжении . Расчетный диаметр резьбы болта по формуле: . Принимаем резьбу М20 с шагом р=2,5 мм, для которой |
25) Решение. Для определения внутренних усилий разбиваем прямолинейный брус на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и точкам приложения сосредоточенных сил. Из рассмотрения рис. а определяем, что брус необходимо разбить на четыре участка. Проводим сечение I – I. Отбросим верхнюю часть бруса, ее действие заменим нормальной силой N1 (рис. б). Запишем уравнение равновесия, проектируя силы на ось бруса: откуда N1 = F. Очевидно, что на всем первом участке ( ) нормальная сила N1 постоянна по величине. Откладываем в масштабе значение нормальной силы N1 = F в пределах участка I – I (рис. е). Проводим сечение II – II и, отбрасывая верхнюю часть бруса, заменяем ее действие нормальной силой N2 (рис. в). Проектируем все силы на ось бруса: откуда N2 = –F. Аналогично находим нормальные силы в сечении III – III (рис. г): откуда N3 = –F и в сечении IV – IV (рис. д): откуда N4 = 0. Откладывая в масштабе значения нормальных сил N2, N3, N4 в пределах соответствующих участков, получаем эпюру нормальных сил (рис. е). Полученную таким путем эпюру принято штриховать прямыми линиями, перпендикулярными к оси бруса. Каждая такая линия в принятом масштабе дает величину нормальной силы в соответствующем поперечном сечении бруса. Знак «плюс» показывает, что в пределах данного участка – растяжение, а знак «минус» – сжатие. Для построения эпюры нормальных напряжений воспользуемся формулой для каждого участка: Эпюра нормальных напряжений (рис. ж) показывает, что наибольшего значения нормальные напряжения достигают в пределах третьего участка (участок III).
|
|||||
25) Решение: Силу Р раскрадываем на две составляющие силы, соответствующие её проекциям на координатные оси. Распределённую нагрузку заменяем сосредоточенной силой Q Составляются уравнения равновесия статики, используется I – основная форма условий равновесия, в которой равны нулю: проекции главного вектора на координатные оси и главный момент относительно произвольного центра (1) ; (2) ; (2) . (3)Из уравнения (1) определяется составляющая реакции связи в точке А – Из уравнения (2) находится составляющая реакции связи в точке А – Из уравнения (3) находится реактивный момент связи в точке А – Проверка: Для проверки составляется уравнение равновесия моментов относительно произвольной точки, например, В, через которую не проходит линия действия ни одной силы. Ответ: кН.м .Знак минус у силовых факторов означает то, что они в действительности направлены в сторону, противоположную той, которая указана на расчётной схеме. |
26) Решение: Допустимое напряжение при растяжении . Расчетный диаметр резьбы болта по формуле: . Принимаем резьбу М20 с шагом р=2,5 мм, для которой |
|||||
Вариант 27 |
Вариант 28 |
|||||
Часть А |
Часть А |
|||||
1 |
3 |
1 |
1 |
|||
2 |
2 |
2 |
3 |
|||
3 |
4 |
3 |
2 |
|||
4 |
3 |
4 |
3 |
|||
5 |
1 |
5 |
1 |
|||
6 |
3 |
6 |
1 |
|||
7 |
3 |
7 |
3 |
|||
8 |
2 |
8 |
2 |
|||
9 |
2 |
9 |
2 |
|||
10 |
1 |
10 |
3 |
|||
11 |
2 |
11 |
1 |
|||
12 |
2 |
12 |
1 |
|||
13 |
2 |
13 |
2 |
|||
14 |
3 |
14 |
3 |
|||
15 |
2 |
15 |
1 |
|||
16 |
3 |
16 |
4 |
|||
17 |
2 |
17 |
1 |
|||
18 |
1 |
18 |
3 |
|||
19 |
2 |
19 |
3 |
|||
20 |
2 |
20 |
1 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-d; 2-d; 3-a; 4-c; |
21 |
1-в; 2-д; 3-г; 4-а; 5-б |
|||
22 |
1-a;2-b;3-c;4-d |
22 |
1-b;2-f; 3-a; 4-g; 5-I; 6-d; 7-e; 8-c |
|||
23 |
1-b;2-c;3-a |
23 |
1-a; 2-c; 3-b |
|||
Часть С |
Часть С |
|||||
25)
|
24)
|
|||||
25) Решение: Принимаем суммарный статистический момент площади рабочих поверхностей . Прочность неподвижного соединения проверяем по напряжениям смятия. Для соединений с незакаленными поверхностями при спокойной нагрузке принимаем допускаемое напряжение на смятие . Расчетное напряжение смятия шлицев по формуле . Условие прочности соединения удовлетворяются. |
25) Решение: Рассмотрим равновесие балки. Проведем координатные оси х и у, и изобразим действующие на балку силы и реакции опор. Для определения YA составим уравнение суммы моментов относительно опоры В: Σ МВ (Fi) = 0 -YA ·(l-а) - m + F· sin α ·( l – a – b) – q · а·а/2 = 0 Откуда: YA =( F· sin α ·( l – a – b) ) – m – q · а·а/2 ) / l-а =(34 · 0 ,7 9 -15 -3· 2· 1)/ /12 = (214,2 – 15 - 6) /12 = 16,1 кН. Для определения YВ составим уравнение суммы моментов относительно опоры А: Σ МА (Fi) = 0 – m -F· sin α · b + YВ · (l-а) - q · а · (l-а/2)= 0 Откуда: YВ =( m + F· sin α · b + q · а · (l-а/2)) / (l-а) = (15+34· 0,7· 3+3· 2· (14-1)) / 12 = =(15+71,4+78) / 12 = 164,4/12 = 13,7 кН. Для определения ХВ составим уравнение суммы проекций на ось х: Σ Fiх = 0 - ХВ + F· соs α = 0 откуда: ХВ = F· соs α = 34 · соs 450 = 23,8 кН. Проверка: Σ Fi у= 0 YA + YВ - F· sin α - q·а = 0 16,1 – 23,8 + 13,7 – 6 =0 |
|||||
26) Решение. 1. Используя формулу , для каждого из 3-х участков получим (рис. а): сечение 1 – 1 = – 4000 кг = –40 кН, сечение 2 – 2 = – 4000 + 3000 = –1000 кг = –10 кН, сечение 3 – 3 = – 4000 + 3000 + 8000=7000кг = 70 кН. 2. Проводим рядом с брусом ось, параллельную его продольной оси, и, выбрав масштаб, откладываем по длине каждого участка найденные значения продольных сил , и , т.е. строим эпюру N (рис. б). 3. Определяем опасное сечение – сечение, в котором нормальные напряжения максимальны (для пластичных материалов берем по абсолютной величине), т.е. ,где А – площадь поперечного сечения бруса. В нашем случае для всех трех участков площадь поперечного сечения А постоянна и по абсолютной величине N3>N2>N1. Опасное сечение – любое сечение участка 3, где = 7000 кг = 70 кН. Тогда из условия прочности на растяжение и сжатие для расчета площади поперечного сечения применим формулу ; .Отсюда
|
26) Решение: момент на ведущем валу равен . Диаметр малого шкива определяем по формуле: . По ГОСТ 17383-73 округляем до ближайшего меньшего значения. Принимаем D₁=315мм. Определяем диаметр большего шкива по формуле: . Принимаем по стандарту D₂=800мм. Определяем скорость ремня по формуле: |
|||||
Вариант 29 |
Вариант 30 |
|||||
Часть А |
Часть А |
|||||
1 |
1 |
1 |
1 |
|||
2 |
2 |
2 |
3 |
|||
3 |
2 |
3 |
2 |
|||
4 |
1 |
4 |
1 |
|||
5 |
3 |
5 |
2 |
|||
6 |
1 |
6 |
1 |
|||
7 |
3 |
7 |
2 |
|||
8 |
1 |
8 |
2 |
|||
9 |
1 |
9 |
3 |
|||
10 |
3 |
10 |
4 |
|||
11 |
1 |
11 |
2 |
|||
12 |
3 |
12 |
2 |
|||
13 |
3 |
13 |
2 |
|||
14 |
2 |
14 |
2 |
|||
15 |
1 |
15 |
4 |
|||
16 |
1 |
16 |
4 |
|||
17 |
1 |
17 |
4 |
|||
18 |
2 |
18 |
2 |
|||
19 |
1 |
19 |
3 |
|||
20 |
1 |
20 |
2 |
|||
Часть Б |
Часть Б |
|||||
21 |
1-b;2-f; 3-a;4-g;5-I; 6-d; 7-e;8-c |
21 |
1-a; 2-d; 3-c; 4-b |
|||
22 |
1-d;7-e;8-c |
22 |
1-b; 2-a; 3-c |
|||
23 |
1-в; 2-д; 3-г; 4-а; 5-б |
23 |
1-д; 2-б; 3-а; 4-г; 5-в |
|||
Часть С |
Часть С |
|||||
24) Решение: Принимаем суммарный статистический момент площади рабочих поверхностей . Прочность неподвижного соединения проверяем по напряжениям смятия. Для соединений с незакаленными поверхностями при спокойной нагрузке принимаем допускаемое напряжение на смятие . Расчетное напряжение смятия шлицев по формуле . Условие прочности соединения удовлетворяются. |
24)
|
|||||
25)
|
25) Решение: Определяем допускаемое напряжение для сварного шва. . По формуле найдем ширину полос : . Округляем до параметрического ряда и принимаем b=120 мм. Условие прочности шва . Условие прочности шва соблюдается (142,4 МПа <144 МПа). |
|||||
26) 2. Изобразим оси координат x и y 3.Силу F заменяем ее составляющими и .Равнодействующая qСD равномерно распределенной нагрузки, приложенная в точке пересечения диагоналей прямоугольника переносится по линии своего действия в середину участка CD, в точку К. 4. Освобождаем балку от опор, заменив их опорными реакциями. 5. Составляем уравнения равновесия статики и определяем неизвестные реакции опор. a) Из уравнения моментов всех действующих на балку сил, составленного относительно одной из точек опор, сразу определяем одну из неизвестных вертикальных реакций:
кН b) Определяем другую вертикальную реакцию:
кН c) Определяем горизонтальную реакцию: ; кН 6. Проверяем правильность найденных результатов: . Условие равновесия выполняется, следовательно, реакции опор найдены верно. |
26)
1. Определяем внутренние продольные силы. Имеем два силовых участка длиной (а + b) и c. Для первого участка, имеем = = 15·103 кг = 150 кН (растяжение); для второго участка: = – = 15 – 20 = –5 кг = –50 кН (сжатие). Выбираем масштаб и строим эпюру (рис. б). 2. Вычисляем нормальные напряжения. На участках а и b площадь поперечного сечения одинакова и равна 2А=20 см2. Тогда
на участке с:
Выбираем масштаб и строим эпюру .
|
|||||

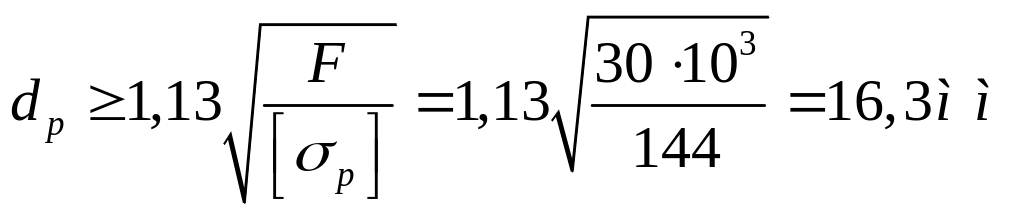 .
Принимаем резьбу М20 с шагом р=2,5 мм,
для которой
.
Принимаем резьбу М20 с шагом р=2,5 мм,
для которой



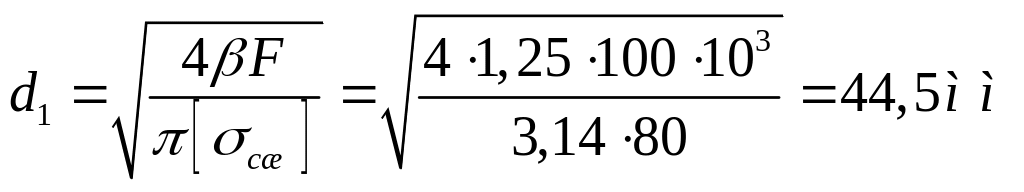 2)
По ГОСТ 9484-81 находим с ближайшим
большим d₁
: d=60
мм;d₁
= 51мм; d₂=56;
ρ=8 мм. 3) Определим необходимую высоту
гайки из расчета резьбы на изностойкость
2)
По ГОСТ 9484-81 находим с ближайшим
большим d₁
: d=60
мм;d₁
= 51мм; d₂=56;
ρ=8 мм. 3) Определим необходимую высоту
гайки из расчета резьбы на изностойкость