§ Стационарный режим движения в системе с одной степенью свободы.

_{Движение системы, которое получится после затухания собственных колебаний, называют установившимся или стационарным режимом движения.}

_{Уравнение движения в случае гармонического возмущения имеет вид:}

_{ω – частота возмущающей силы.}

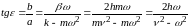₍₁₎

_{Справка:}

_{Динамический коэффициент:}

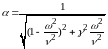
_{Статические перемещения груза при действии амплитудного значения возмущающей силы:}

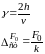
_{В уравнении (1) А,В – постоянные интегрирования не входят, то есть стационарный режим не зависит от начальных условий, а определяется только приложенными силами. Система колеблется с частотой возмущающей силы ω, фаза перемещения х отстает от фазы возмущающей силы на величину ε, амплитуда колебаний .}

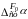_{Амплитуда пропорциональна α, то есть зависит от 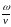а зависит от то есть от сопротивления движению.}

_{Рассмотрим несколько случаев (при различном h – коэффициенте затухания) и построим АЧХ.}

1. _h=0,

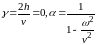
2. _{в это время амплитуда (то есть половина от )}

3. 

_{В инженерных конструкциях γ<<1. Так, для стальной балки γ≈0,005 при этом α≈200 при ω=υ. Поэтому в конструкциях подвижного состава устанавливают параллельно с рессорным подвешиванием специальные приспособления, которые называют демпферами (гасителями колебаний – наиболее распространены сухого трения и гидравлические).}

_{Кроме оценки амплитуды вынужденных колебаний рассмотрим зависимость фаз между возмущающей силой и перемещением груза (опаздывает на}

1. 

2. _{При ε зависит от ω}

3. 

_При

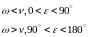
_{Если возмущающая сила является более сложной периодической функцией времени, то ее представляют в виде тригонометрического полинома:}

§ Переходные (неустановившиеся) режимы движения.

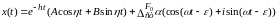
_{В случае:}

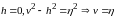
_{Считаем, что до приложения возмущающей силы, груз находится в равновесии, поэтому начальные условия:}

1. _При

2. _При

_{Такие начальные условия называют нулевыми.}

_{Определяем А и В.}

_{Воспользуемся уравнением (1):}

Воспользуемся уравнением (2):

При

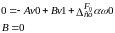
Таким образом при этих начальных условиях решение будет:

Справка:

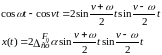
Если 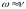(значения близки).

величина малая, а

Движение груза будет приближенно представлять собой гармоническое колебание с частотой, близкой к ω и с переменной амплитудой равной:

Время изменения амплитуды:

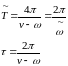
Такое движение называют биениями.

Что будет при резонансе? Когда ω приближается к υ.

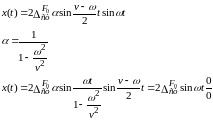
При ω→υ получаем неопределенность (0/0).

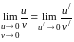
Берем производную числителя и знаменателя по ω.

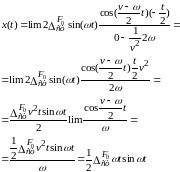
Это и будет уравнение движения грза при резонансе.

Время изменения амплитуды биений Т при ω=υ обращается в бесконечность.

Амплитуды колебаний при резонансе возрастают пророрционально времени.

Если

Резонанс имеет место при всех ω равных υ.