§8. Собственные затухающие колебания системы с одной степенью свободы

В предыдущем вопросе мы рассмотрели движение линейных систем с одной степенью свободы без сопротивления движению. Такая идеализация полезна, но в реальных системах всегда есть сопротивление движению.

Рассмотрим собственные колебания линейной системы с одной степенью свободы, то есть

_{, где v – частота собственных свободных колебаний}

_{, где h – коэффициент затухания.}

_{Математическая модель принимает вид:}

Введем новую зависимую переменную:

_Тогда

_{Подставим в наше уравнение:}

_{при любом t, следовательно}

_{Обозначим ,тогда .}

_{Возможны три случая:}

4. _{тогда периодические затухающие колебания.}

_{Решение уже отыскивалось.}

_{, а}

_{Здесь частота собственных свободных затухающих колебаний.}

_{А,В – постоянные интегрирования, находят из начальных условий.}

_{В решении в скобках стоят периодические функции времени, следовательно, движение – колебательное, но перед скобкой находится множитель , так что амплитуды колебаний убывают во времени.}

_{График такого движения имеет вид:}

_{Такое движение является периодическим и называется затухающими колебаниями.}

_{Понятие периода затухающих колебаний 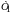вводят для переменной z, то есть ,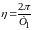} или .

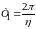_{Частота затухающих колебаний}

При

Исследуем скорость убывания амплитуд:

Для этого вычислим и - два момента времени отличаются на период.

Справка:

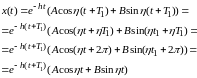
Найдем отношение первой амплитуды ко второй

Возьмем натуральный логарифм

логарифмический декремент затухания, это логарифм отношения предыдущей к последующей амплитуде колебаний.

Декремент характеризует быстроту затухания.

Чем выше тем быстрее идет затухание.

Иногда вводят еще одну динамическую характеристику добротность системы.

Оценим декремент затухания для

То есть при отношении частоты собственных свободных и затухающих колебаний практически равны, а последующая амплитуда колебаний практически в два раза меньше предыдущей. Таким образом вязкое трение существенно влияет на амплитуду колебаний и поэтому его нужно учитывать.

5. Лимитационное (апериодическое) движение.

Рассмотрим собственные колебания линейной системы с одной степенью свободы.

Справка:

Мы перешли к новой координате дифференциальное уравнение приняло вид

Если то

Решение ищут в гиперболических функциях

Справка:

Тогда:

Подставим в уравнение

Окончательно:

Это уравнение апериодического или лимитационного движения.

Форма движения зависит от начальных условий.

Тогда

Решение ищется в виде

Помним, что

Апериодическое.

То есть при движение периодическое колебательное (периодические затухающие колебания);

апериодическое.

Случай называется критическим, а соответствующий коэффициент вязкого тела обозначают

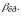
Установлено, что при 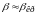в рессорах с пружинах возникают очень большие силы, так как упругие элементы заклинивают и не обемпечивают упругие свойства.

Колебания должны быть колебательный процесс;

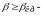лимитационное движение.

_{При проектировании принимают} . Для демпферов вязкого трения