§6. Колебания систем с одной степенью свободы

Рассмотрим механическую систему в виде груза массой m, висящую на пружине с жесткостью k и гидравлического демпфера с коэффициентом демпфирования β.

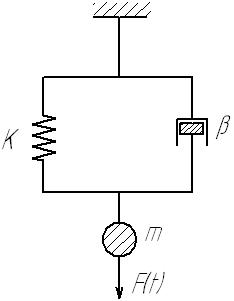Механическая система имеет бесконечное число степеней свободы, так как пружина – упругое тело и перемещения ее частей должны удовлетворять условию неразрывности деформаций.

Для исследования колебаний такой системы нужно ввести соответствие идеализации:

Будем считать, что груз может двигаться только в вертикальном направлении; массой пружины и демпфера по сравнению с массой груза можно пренебречь; начальное отклонение и скорость груза заданы.

Положение груза, а следовательно и конфигурации системы, определяется одной координатой – его отклонением от положения равновесия, а состояние системы – координатой груза x и скоростью груза , поэтому при принятых идеализациях система имеет одну степень свободы.

Уравнение движения простых систем можно составлять на основании принципа Даламбера: «Решение задач динамики можно свести к решению задачи статики, если кроме действующих сил добавить фиктивную силу инерции равную произведению массы на ускорение и направленную в сторону противоположную ускорению».

Рассмотрим равновесие массы m, вырезанной из системы:

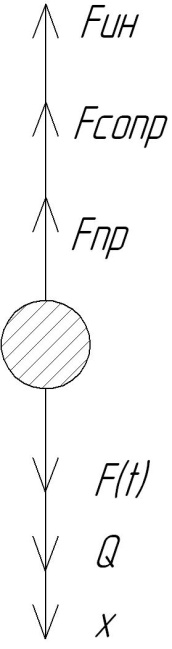
фиктивная сила инерции

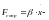сила вязкого сопротивления

восстанавливающая сила

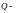вес груза

₍₅₎

_{линейное дифференциальное уравнение.}

§7. Собственные свободные колебания линейных систем с одной степенью свободы

_{Положим, что внешняя сила 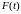равна нулю и система, выведенная из положения равновесия в начальный момент, далее представлена самой себе. Такие колебания называются собственными.}

_{Введем еще одну идеализацию: положим, что сопротивление демпфера в механической системе равно нулю. Такие колебания называются свободными.}

_{Исследование собственных свободных колебаний представляет важный практический интерес, так как характеристики этих колебаний (частоты и формы) полностью определяют индивидуальные динамические свойства механической системы и имеют первостепенное значение также и при анализе вынужденных колебаний.}

_{Кстати, резонанс – явление неограниченного возрастания амплитуды вынужденных колебаний. Имеет место при совпадении частоты возмущающей силы с частотой собственных свободных колебаний.}

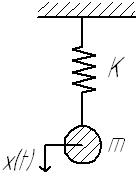_Итак,

_{Задано: 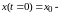начальное отклонение массы от положения статического равновесия.}

_{начальная скорость.}

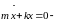_{математическая модель, описывающая собственные свободные колебания системы с одной степенью свободы.}

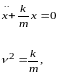_{тогда 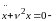линейное однородное дифференциальное уравнение второго порядка.}

_{Решение:}

_{где А и В - постоянные интегрирования, определяются из начальных условий задачи.}

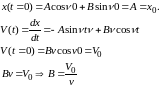
_Итак,

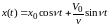
_{Этому решению можно придать иную форму.}

_{Положим, тогда}

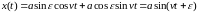
_{Справка:}

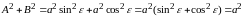
_{В этом решении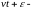} фаза колебаний,

начальная фаза,

_{а - амплитуда колебаний (наибольшее отклонение груза от положения равновесия)}

_{Так как sin- функция периодическая, то и движение груза относительно положения равновесия периодическое.}

_{Аргументом sin является функция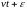} . Такое движение называют гармоническим. Промежуток времени T, в течении которого груз совершает одно полное колебание, называют периодом колебаний.

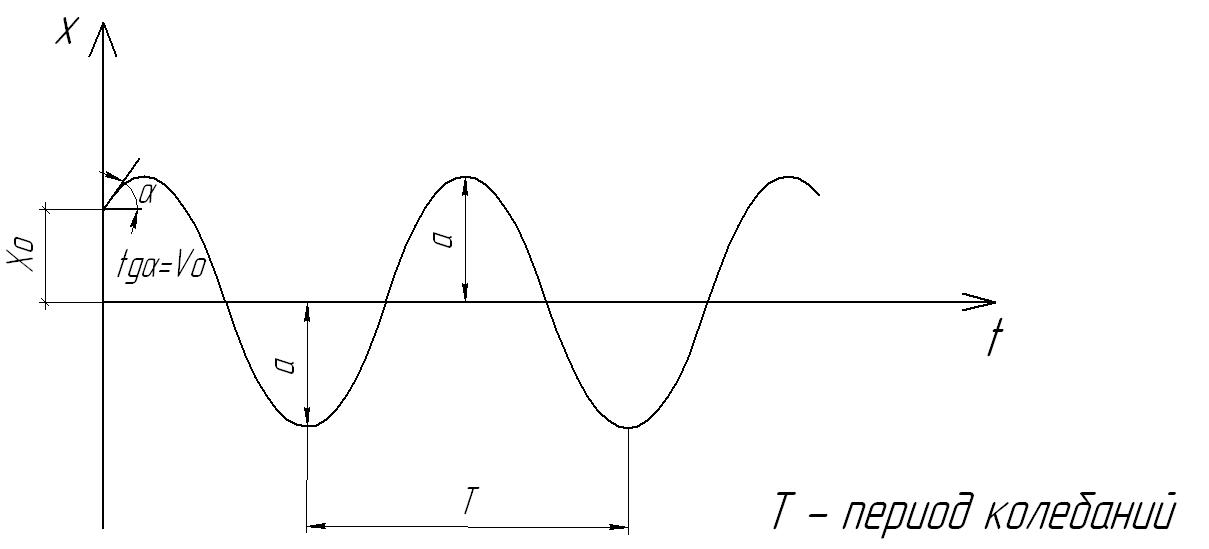
Груз совершает полное колебание, если аргумент изменяется на .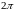

где v – круговая частота колебаний – количество полных колебаний, которые совершает груз за секунд.

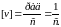
Вспомним, что 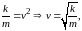то есть частота собственных свободных колебаний не зависит от начальных условий, а определяется только массой груза и жесткостью пружины.

Рассмотрим еще линейную частоту, равную числу колебаний за 1 секунду, то есть величину обратную периоду Т колебаний.

Частоту собственных свободных колебаний иногда удобнее определить через 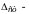удлинение пружины, которое получается, если груз свободно висит на ней:

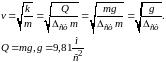
Пружину в механической системе можно заменить любым упругим телом, подчиняющимся закону Гука, если массой этого тела пренебречь.

Пример:

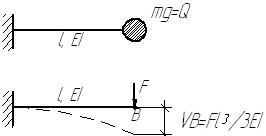
_{Сравним выражение при условии эта схема эквивалентна ранее рассматриваемой.}