§3. Составление механической модели
Любая реальная механическая система состоит из бесконечного числа материальных точек; так как связи между ними не являются абсолютно жесткими, то число степеней свободы такой системы бесконечно велико.
В общем случае решить такую задачу точно невозможно и приходится становиться на путь упрощения расчетной модели и ограничения числа степеней свободы.
При этом имеется в виду пренебрежения малозначительными свойствами реальной системы и сохранение в модели лишь существенных степеней свободы.
Можно указать три основных способа выбора расчетной схемы:
Относительно менее массивные части системы полагаются вовсе лишенными массы и представляются в виде безинерционных элементов, а наиболее жесткие части конструкции принимаются за абсолютно твердые тела.
Система представляется в виде сосредоточения податливости непрерывной системы в конечном числе точек. При этом система представляется в виде совокупности упруго сочлененных жестких элементов.
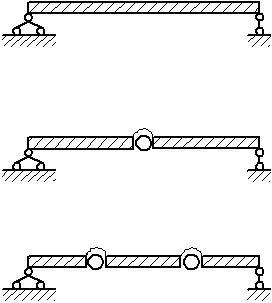
Этот способ основан на априорных предположениях об изменении конфигурации системы в процессе колебаний.
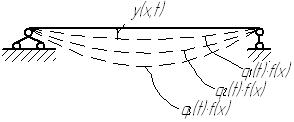
или
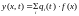
Здесь
функция,
описывающая ось балки,
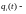функция
времени, являющаяся неизвестной в
задаче.
При
этом
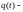обобщенная
координата.
§4. Силы, действующие при колебаниях
Можно выделить три основных типа сил:
Силы, зависящие от времени;
Силы, зависящие от положения системы;
Силы, зависящие от скорости точки.
Силы, зависящие от времени, называются обобщенными возмущающими силами
и служат причиной вынужденных колебаний.
Источники возникновения возмущающих
сил разнообразны: вибраторы, удар о
стык рельса, случайные функции времени.Силы, зависящие от положения системы, называются обобщенными позиционными силами.
Силы, зависящие от скорости, называются обобщенными силами трения и направлены в сторону противоположную движению.
Чаще всего эти силы препятствуют развитию колебаний. В этом случае они называются диссипативными. Силы трения возникают в сочленении звеньев, в опорах, в направляющих механической системы, а также и в материале звеньев. Существенное значение имеет вид зависимости обобщенной силы трения от обобщенной скорости. Наиболее часто используются следующими зависимостями:
– сила линейно-вязкого трения
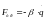
– кулонова сила трения
– сила нелинейно-вязкого трения
При составлении механической модели большое значение имеет разумное пренебрежение несущественными параметрами и силами, а для учитываемых – правильная механизация свойств системы и сил.
§5. Колебания линейных и нелинейных систем
Колебания механических систем описываются дифференциальными уравнениями. Например, для системы с одной степенью свободы движение описывается уравнением второго порядка:
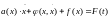(1)
Дифференциальное уравнение нелинейное, поэтому и система называется нелинейной. В настоящее время нет общих методов решения систем дифференциальных уравнений, поэтому решение таких задач затруднительно. Часто вводят идеализации, например:
Пружина подчиняется закону Гука, то есть реакция пропорциональна удлинению
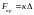(2)
Сопротивление демпфера пропорционально скорости его удлинения (вязкое трение).
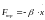(3)
В этих случаях коэффициенты уравнения становятся постоянными и уравнение (1) принимает вид линейного дифференциального уравнения:
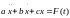(4)
Системы, описываемые линейными уравнениями, называют линейными.